
Видео к теме 1; 2; 3; 4
Задача 1. Найдите площадь круга, длина окружности которого равна $22\sqrt{\pi}.$

Решение: + показать
Длина окружности вычисляется по формуле $\color{red}C=2\pi R$.
Поэтому $22\sqrt{\pi}=2\pi R.$
Откуда $R=\frac{11}{\sqrt{\pi}}.$
Площадь круга вычисляется по формуле $\color{red}S=\pi R^2.$
Тогда $S=\pi\cdot (\frac{11}{\sqrt{\pi}})^2=121.$
Ответ: $121.$
Задача 2. Площадь круга равна $\frac{441}{\pi}$. Найдите длину его окружности.

Решение: + показать
Площадь круга вычисляется по формуле $\color{red}S=\pi R^2.$
Значит, $\frac{441}{\pi}=\pi R^2;$
Откуда $R^2=\frac{441}{\pi^2};$
$R=\frac{21}{\pi};$
Длина окружности вычисляется по формуле $\color{red}C=2\pi R$.
Поэтому $C=2\pi\cdot \frac{21}{\pi}=42.$
Ответ: $42.$
Задача 3. Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны $\frac{51}{\sqrt{\pi}}$ и $\frac{47}{\sqrt{\pi}}.$
Решение: + показать
Площадь кольца – есть разность площадей большего и меньшего кругов.
Площадь большего круга: $S_1=\pi R_1^2=\pi\cdot (\frac{51}{\sqrt{\pi}})^2=51^2;$
Площадь меньшего круга: $S_2=\pi R_2^2=\pi\cdot (\frac{47}{\sqrt{\pi}})^2=47^2;$
Тогда площадь кольца: $S=S_1-S_2=51^2-47^2=(51-47)(51+47)=392.$
Ответ: $392.$
Задача 4. На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 4. Найдите площадь заштрихованной фигуры. Видеорешение*

Решение: + показать
Как и в предыдущей задаче искомая площадь фигуры – есть разность площадей кругов (большого и малого).
Исходя из чертежа, можно сказать, что радиус большого круга вдвое больше радиуса меньшего.
При этом известно, что площади кругов относятся как квадраты их радиусов. Значит, площадь большего круга равна $4\cdot 4=16.$
Наконец, искомая площадь: $16-4=12.$
Ответ: $12.$
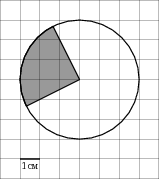
Задача 5. На клетчатой бумаге с клетками размером 1 см x 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. В ответе запишите $\frac{S}{\pi}$. Видео*
Решение: + показать
Радиус окружности на рисунке составляет 3 единицы. Значит площадь круга есть $S=\pi R^2=\pi \cdot3^2=9\pi.$
Рассмотрим треугольник $ABO:$
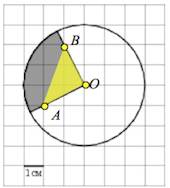
В нем $BO=\sqrt{1^2+2^2}=\sqrt5;$
$AO=\sqrt{1^2+2^2}=\sqrt5;$
$AB=\sqrt{1^2+3^2}=\sqrt{10};$
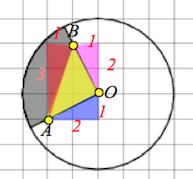
То есть мы замечаем, что треугольник $ABO$ – прямоугольный, так как $AB^2=AO^2+BO^2.$
А значит, закрашенный сектор составляет четверть круга.
Поэтому площадь $S$ сектора есть $\frac{S_{krug}}{4}=\frac{9\pi}{4}.$
В ответе нужно указать $\frac{S}{\pi}$, то есть $\frac{9\pi}{4\pi}=\frac{9}{4}=2,25.$
Ответ: $2,25.$
Задача 6. Найдите площадь сектора круга радиуса 6, длина дуги которого равна 3.
Решение: + показать
Пуст $x$– искомая площадь сектора

Ответ: $9.$
Задача 7. Площадь сектора круга радиуса 3 равна 15. Найдите длину его дуги.

Решение: + показать
Пусть $x$ – длина дуги сектора, которую ищем

Ответ: $10.$
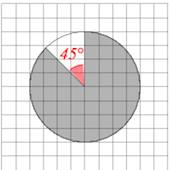
Задача 8. Найдите центральный угол сектора круга радиуса $\frac{24}{\sqrt{\pi}}$, площадь которого равна 96. Ответ дайте в градусах.

Решение: + показать
Пусть $x$ – искомый центральный угол сектора, всему кругу сопоставляем центральный угол в $360^{\circ}$:

Ответ: $60.$
Задача 9. На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 56?

Решение: + показать
Так как сектор занимает $\frac{7}{8}$ площади круга, то площадь круга соответственно составляет $\frac{8}{7}$ площади сектора, то есть $\frac{8\cdot 56}{7}=64.$
Ответ: $64.$
Задача 10. На клетчатой бумаге с клетками размером 1 см x 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. В ответе запишите $\frac{S}{\pi}$. Видео
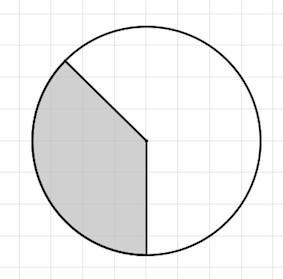
Решение: + показать
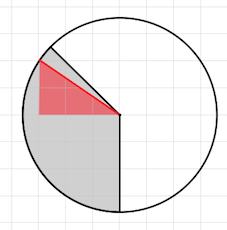 Радиус круга, как видно из рисунка, равен $\sqrt{2^2+3^2}=\sqrt{13}.$
Радиус круга, как видно из рисунка, равен $\sqrt{2^2+3^2}=\sqrt{13}.$
Тогда площадь круга равна $\pi R^2=13\pi.$
Помеченный же сектор занимает $\frac{3}{8}$ часть круга.
Тогда площадь сектора $S$ равна $13\pi \cdot\frac{3}{8}=4,875\pi.$
Наконец, $\frac{S}{\pi}=\frac{4,875\pi}{\pi}=4,875.$
Ответ: $4,875.$
Задача 11. На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите радиус описанной около него окружности.
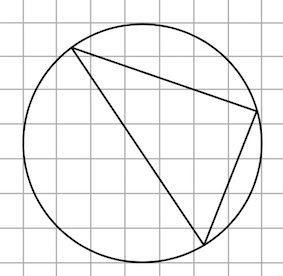
Решение: + показать
Хорошо видно, что окружность вписана в квадрат со стороной $7,$ стало быть радиус окружности равен $3,5.$
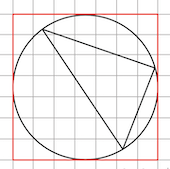
Ответ: $3,5.$
Задача 12. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC Ответ дайте в градусах.
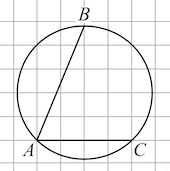
Решение: + показать
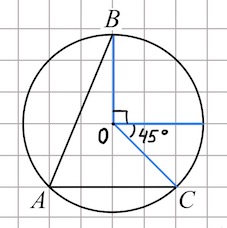
Градусная мера дуги $BC$ равна градусной мере центрального угла $BOC.$ При этом $\angle BOC=135^{\circ}.$
Ответ: $135.$

Вы можете пройти тест
![]()






















 Радиус круга, как видно из рисунка, равен $\sqrt{2^2+3^2}=\sqrt{13}.$
Радиус круга, как видно из рисунка, равен $\sqrt{2^2+3^2}=\sqrt{13}.$

Задача 5:
“То есть мы замечаем, что треугольник ABO – прямоугольный, так как [latexpage] $AB^2=AO^2+BO^2$ – а если я не такой внимательный и не способен это заметить? может быть есть другой способ?
Придется быть внимательным!.. Главное – зацепиться за все «хорошие» точки (вершины клеточек)…
Хорошо, спасибо! По обоим вопросам всё ясно :)
Задача 4: куда пропало Pi ?
А оно и не пропадало… Мы просто исходили из того, что раз нам известна площадь меньшего круга 4, то большего – в 4 раза больше. Все!
очень тяжело даются задачи с секторами…
Вопросы конкретные есть?
да вроде нет, просто туго доходит решение задач 6,7 и 8… как я понял они решаются по пропорции
Да, все через пропорцию. Следовало бы четче мне дать объяснения… Возможно, подправлю, будет время…
… Добавила
Вообще отлично! Теперь думаю каждый поймёт :) Спасибо!
Как в первой задаче получилось R= 11/корень из pi? у нас же получается, что 22корень из pi= 2piR=> R=22 корень из pi/2pi=> 11 корень из pi/pi не так ли?
Все так, только вы не учли, что [latexpage]$\frac{\sqrt{\pi}}{\pi}=\frac{1}{\sqrt{\pi}}$.
И как еще определить какую часть занимает сектор от круга? я подзабыл чего-то:)
Если известен угол сектора, поделите его на 360°. Узнаете часть.