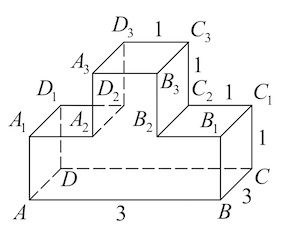
Задача 1. Найдите квадрат расстояния между вершинами $D$ и $C_1$ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
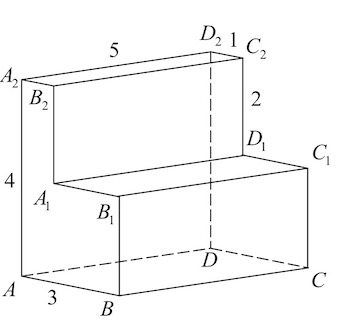
Решение: + показать
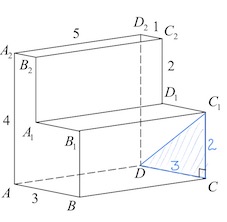
Из прямоугольного треугольника $DCC_1$ по т. Пифагора
$DC_1^2=DC^2+CC_1^2;$
$DC_1^2=3^2+2^2;$
$DC_1^2=13.$
Ответ: $13.$
Задача 2. Найдите расстояние между вершинами $B$ и $C_2$ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
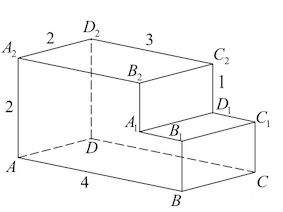
Решение: + показать
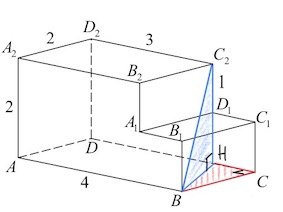
Пусть $C_2D_1$ пересекается с $DC$ в точке $H.$
Из прямоугольного треугольника $BCH$ по т.Пифагора:
$BH^2=BC^2+CH^2;$
$BH^2=2^2+1^2=5.$
Из прямоугольного треугольника $BHC_2$ по т. Пифагора:
$BC_2=\sqrt{BH^2+HC_2^2}=\sqrt{5+2^2}=3.$
Ответ: $3.$
Задача 3. Найдите расстояние между вершинами $B_1$ и $D_2$ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
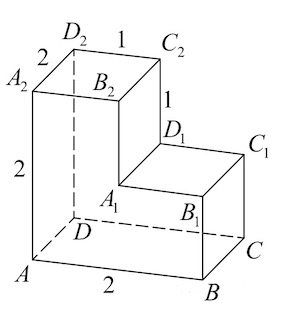
Решение: + показать
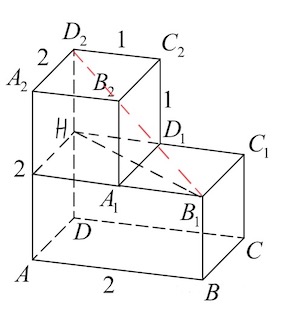
Продлим отрезок $C_1D_1$ за $D_1$ до пересечения с ребром $DD_2$ в точке $H.$
Из прямоугольного треугольника $HC_1B_1$ по т. Пифагора:
$HB_1^2=B_1C_1^2+HC_1^2;$
$HB_1^2=2^2+2^2=8.$
Из прямоугольного треугольника $HD_2B_1$ по т. Пифагора
$B_1D_2=\sqrt{HD_2^2+HB_1^2};$
$B_1D_2=\sqrt{1^2+8}=3.$
Ответ: $3.$
Задача 4. Найдите квадрат расстояния между вершинами $D_3$ и $B$ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
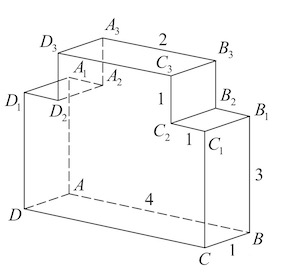
Решение: + показать
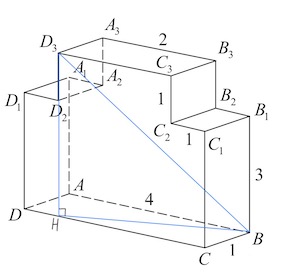
Продлим $D_3D_2$ до пересечения с $DC$ в точке $H.$
Из трeугольника $BCH$ по т. Пифагора:
$BH^2=BC^2+CH^2;$
$BH^2=1^2+3^2=10.$
Из трeугольника $BHD_3$ по т. Пифагора:
$BD_3^2=D_3H^2+BH^2;$
$DB_3^2=4^2+10=26.$
Ответ: $26.$
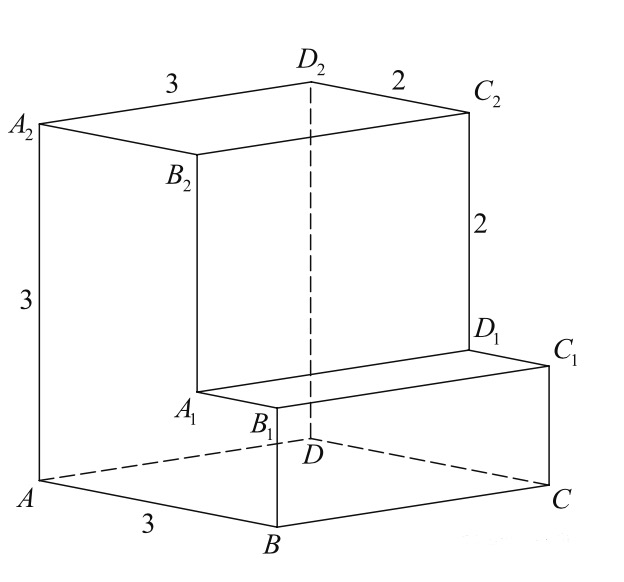
Задача 5. Найдите угол $ACD_2$ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Решение: + показать
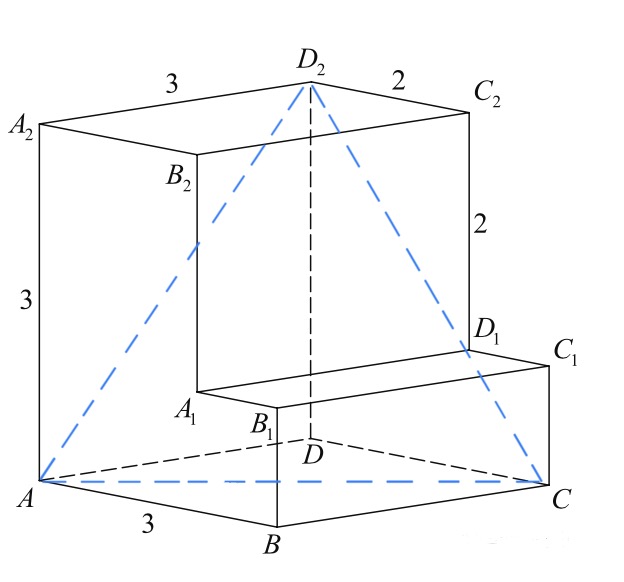
Треугольник $ACD_2$ – равносторонний (каждая сторона – диагональ квадрата $3$x$3$). Все углы в нем, в том числе и угол $ACD_2$ равны по $60^{\circ}.$
Ответ: $60.$
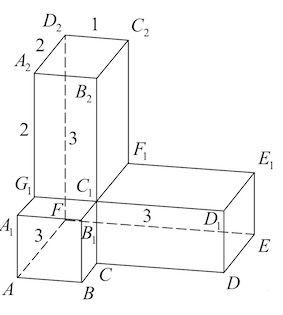
Задача 6. Найдите угол $AD_2E$ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Решение: + показать
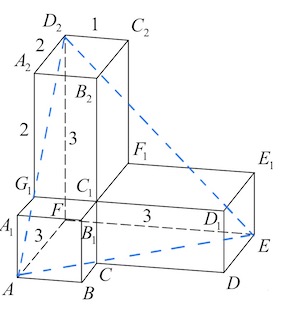
Треугольник $AD_2E$ – правильный (каждая сторона – диагональ квадрата $3$x$3$), поэтому $\angle AD_2E=60^{\circ}.$
Ответ: $60.$
Задача 7. Найдите тангенс угла $ABB_3$ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Решение: + показать
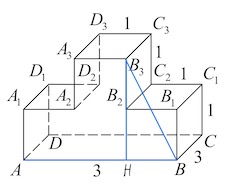
Продлим $B_2B_3$ до пересечения с $AB$ в точке $H.$
Угол $ABB_3$ есть угол $HBB_3$.
Из треугольника $BB_3H:$
$tgHBB_3=\frac{HB_3}{EB};$
$tgHBB_3=\frac{2}{1}=2.$
Ответ: $2.$
 Вы можете пройти тест «Составные многогранники»
Вы можете пройти тест «Составные многогранники»







 Вы можете пройти тест «Составные многогранники»
Вы можете пройти тест «Составные многогранники»








Добавить комментарий