Задача 1. Найдите точку максимума функции $y=x^3-108x+11.$
Решение: + показать
$y’=3x^2-108=3(x^2-36)=3(x-6)(x+6).$
$y’=0\;\Leftrightarrow \;x=\pm 6.$
В соответствии со знаками производной указываем поведение функции:
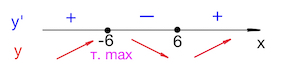
В точке $-6$ возрастание сменяется убыванием, значит $-6$ – точка максимума.
Ответ: $-6.$
Задача 2. Найдите точку минимума функции $y=21x^2-x^3+17.$
Решение: + показать
$y’=42x-3x^2=3x(14-x).$
В соответствии со знаками производной указываем поведение функции:
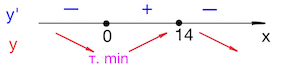
В точке $0$ убывание сменяется возрастанием, значит $0$ – точка минимума.
Ответ: $0.$
Задача 3. Найдите наименьшее значение функции $y=x^3-15x^2+19$ на отрезке $[5;15]$.
Решение: + показать
$y’=3x^2-30x=3x(x-10).$
$y’=0\;\Leftrightarrow \;x=0$ или $x=10.$
В соответствии со знаками производной указываем поведение функции, причем интересует только поведение функции на отрезке $[5;15]$:
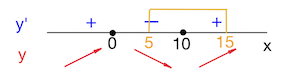
Наименьшее значение функции в данном случае* (см. замечание внизу стр.) совпадает с минимумом функции в точке $x=10$.
$y(10)=10^3-15\cdot 10^2+19=-481.$
Ответ: $-481.$
Задача 4. Найдите наибольшее значение функции $y=2+9x-\frac{x^3}{3}$ на отрезке $[2;6].$
Решение: + показать
$y=9-x^2=(3-x)(3+x).$
В соответствии со знаками производной указываем поведение функции, причем нас интересует только поведение функции на отрезке $[2;6]$:
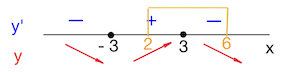
Наибольшее значение функции в данном случае* (см. замечание внизу стр.) совпадает с максимумом функции в точке $x=3$.
$y(3)=2+9\cdot 3-\frac{3^3}{3}=20.$
Ответ: $20.$
Задача 5. Найдите наибольшее значение функции $y=3x^5-20x^3-54$ на отрезке $[-4;-1].$
Решение: + показать
$y’=15x^4-60x^2=15x^2(x^2-4)=15x^2(x-2)(x+2).$
В соответствии со знаками производной указываем поведение функции, причем нас интересует только поведение функции на отрезке $[-4;-1]$:
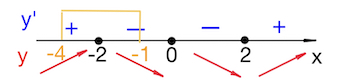
Наибольшее значение функции в данном случае* (см. замечание внизу стр.) совпадает с максимумом функции в точке $x=-2$.
$y(-2)=3\cdot (-32)-20\cdot (-8)-54=10.$
Ответ: $10.$
Задача 6. Найдите наибольшее значение функции $y=-3x^5-6x^3+14$ на отрезке $[-1;8].$
Решение: + показать
$y’=-15x^4-18x^2=-3x^2(5x^2+6).$
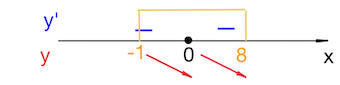
Наибольшее значение на отрезке $[-1;8]$ функция принимает в левом конце отрезка, в точке $-1.$
$y(-1)=3+6+14=23.$
Ответ: $23.$
Задача 7. Найдите точку максимума функции $y=6+12x-2x^{\frac{3}{2}}.$
Решение: + показать
$y’=12-2\cdot \frac{3}{2}\cdot x^{\frac{3}{2}-1}=12-3x^{\frac{1}{2}}=12-3\sqrt x.$
$y’=0\;\Leftrightarrow \;x=16.$
В соответствии со знаками производной указываем поведение функции:
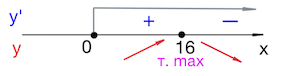
Тогда точка $x=16$ – точка максимума функции.
Ответ: $16.$
Задача 8. Найдите наибольшее значение функции $y=-\frac{2}{3}x\sqrt x+3x+8$ на отрезке $[1;9].$
Решение: + показать
$y’=(-\frac{2}{3}\cdot x^{\frac{3}{2}}+3x+8)’=-\frac{2}{3}\cdot \frac{3}{2}\cdot x^{\frac{1}{2}}+3=3-\sqrt x.$
$y’=0$ при $x=9.$
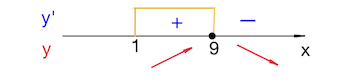
На указанном отрезке функция возрастает, тогда наибольшее значение будет достигнуто в точке $x=9.$
$y(9)=-18+27+8=17$
Ответ: $17.$
Задача 9. Найдите точку минимума функции $y=-\frac{x^2+25}{x}$.
Решение: + показать
Нам предстоит находить производную частного:
$\color{red}(\frac{u}{v})’=\frac{u’v-uv’}{v^2}$.
$y’=(-\frac{x^2+25}{x})’=-\frac{(x^2+25)’\cdot x-(x^2+25)\cdot x’}{x^2}=-\frac{2x^2-x^2-25}{x^2}=$
$=-\frac{x^2-25}{x^2}=-\frac{(x-5)(x+5)}{x^2}.$
$y’=0\;\Leftrightarrow \;x=\pm 5.$
В соответствии со знаками производной указываем поведение функции:
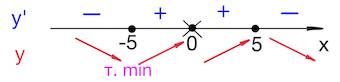
Стало быть, $x=-5$ – точка минимума.
Ответ: $-5.$
Задача 10. Найдите наименьшее значение функции $y=\frac{x^2+900}{x}$ на $[3;40].$
Решение: + показать
$y’=\frac{(x^2+900)’\cdot x-(x^2+900)\cdot x’}{x^2}=\frac{2x^2-x^2-900}{x^2}=\frac{x^2-900}{x^2}=\frac{(x-30)(x+30)}{x^2}.$
$y’=0\;\Leftrightarrow \;x=\pm 30.$
В соответствии со знаками производной указываем поведение функции, причем нас интересует только поведение функции на отрезке $[3;40]$:
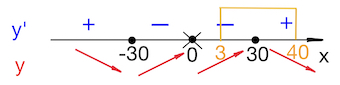
Наименьшее значение функции в данном случае* (см. замечание внизу статьи) совпадает с минимумом функции (в точке $x=30$).
$y(30)=\frac{30^2+900}{30}=60.$
Ответ: $60.$
Задача 11. Найдите точку максимума функции $y=\frac{441}{x}+x+18.$
Решение: + показать
$y’=-\frac{441}{x^2}+1=\frac{x^2-441}{x^2}=\frac{(x-21)(x+21)}{x^2}.$
В соответствии со знаками производной указываем поведение функции:
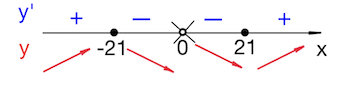 Точка максимума – это $x=-21.$
Точка максимума – это $x=-21.$
Ответ: $-21.$
Задача 12. Найдите точку минимума функции $y=(3x^2-15x+15)e^{x-15}.$
Решение: + показать
$\color{red}(uv)’=u’v+uv’$
$y’=(3x^2-15x+15)’e^{x-15}+(3x^2-15x+15)(e^{x-15})’=$
$=(6x-15)e^{x-15}+(3x^2-15x+15)e^{x-15}=e^{x-15}(6x-15+3x^2-15x+15)=$
$=e^{x-15}(3x^2-9x)=3e^{x-15}x(x-3).$
$y’=0\;\Leftrightarrow \;x=0$ или $x=3.$
В соответствии со знаками производной указываем поведение функции:
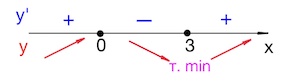
Точка минимума – $x=3$.
Ответ: $3.$
Задача 13. Найдите точку максимума функции $y=(x+11)^2\cdot e^{3-x}.$
Решение: + показать
$\color{red}(uv)’=u’v+uv’$
$y’=((x+11)^2)’\cdot e^{3-x}+(x+11)^2\cdot (e^{3-x})’=$
$=2(x+11)\cdot e^{3-x}+(x+11)^2\cdot e^{3-x}\cdot (-1)=$
$=e^{3-x}(x+11)(2-x-11)=-e^{3-x}(x+11)(x+9).$
В соответствии со знаками производной указываем поведение функции:
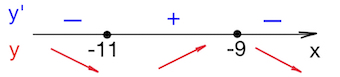
Точка максимума:
$x=-9$.
Ответ: $-9.$
Задача 14. Найдите наименьшее значение функции $y=(x-3)^2(x-6)-1$ на отрезке $[4;6]$.
Решение: + показать
$y’=((x-3)^2)'(x-6)+(x-3)^2(x-6)’=2(x-3)(x-6)+(x-3)^2=$
$=(x-3)(2(x-6)+(x-3))=(x-3)(3x-15).$
$y’=0\;\Leftrightarrow \;x=3$ или $x=5.$
В соответствии со знаками производной указываем поведение функции. Причем нас интересует только отрезок $[4;6].$
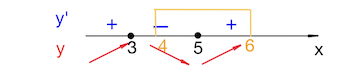
Наименьшее значение функции на отрезке $[4;6]$ совпадает* с минимумом функции в точке $x=5$:
$y(5)=(5-3)^2(5-6)-1=-5.$
Ответ: $-5.$
Задача 15. Найдите наибольшее значение функции $y=ln(x+4)^9-9x$ на отрезке $[-3,5;0].$
Решение: + показать
$y’=(9ln(x+4)-9x)’=\frac{9}{x+4}-9.$
$y’=0\;\Leftrightarrow \;\frac{9}{x+4}-9=0\;\Leftrightarrow \;\frac{9-9x-36}{x+4}=0\;\Leftrightarrow \;x=-3.$
На отрезке $[-3,5;0]$ мы увидим следующие знаки производной, и, соответственно, следующее поведение функции:
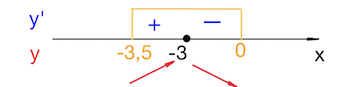
Наибольшее значение функции на отрезке $[-3,5;0]$ совпадает с максимумом функции в точке $x=-3$:
$y(-3)=ln(-3+4)^9-9\cdot (-3)=27.$
Ответ: $27.$
Задача 16. Найдите наименьшее значение функции $y=6x-ln(6x)+17$ на отрезке $[\frac{1}{12};\frac{5}{12}].$
Решение: + показать
$y’=6-\frac{1}{6x}\cdot (6x)’=6-\frac{1}{x}=\frac{6x-1}{x}.$
На отрезке $[\frac{1}{12};\frac{5}{12}]$ мы увидим следующие знаки производной, и, соответственно, следующее поведение функции:
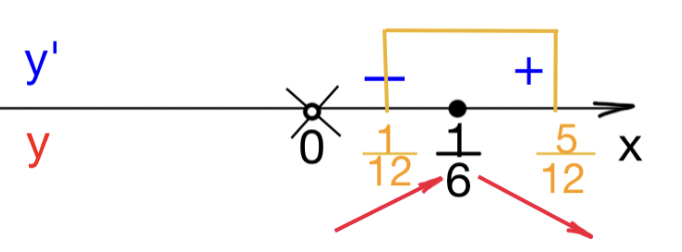
Наименьшее значение функции на отрезке $[\frac{1}{12};\frac{5}{12}]$ совпадает с максимумом функции в точке $x=\frac{1}{6}$:
$y(\frac{1}{6})=6\cdot \frac{1}{6}-ln1+17=18.$
Ответ: $18.$
Задача 17. Найдите наименьшее значение функции $y=2x^2-3x-lnx+13$ на отрезке $[\frac{3}{4};\frac{5}{4}].$
Решение: + показать
$y’=4x-3-\frac{1}{x}=\frac{4x^2-3x-1}{x}=\frac{4(x-1)(x+0,25)}{x}.$
В соответствии со знаками производной указываем поведение функции. Причем нас интересует только отрезок $[\frac{3}{4};\frac{5}{4}].$
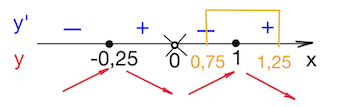
Наименьшее значение функции на отрезке $[\frac{3}{4};\frac{5}{4}]$ совпадает с минимумом функции в точке $x=1$:
$y(1)=2-3-0+13=12.$
Ответ: $12.$
Задача 18. Найдите наименьшее значение функции $y=e^{2x}-11e^x-1$ на отрезке $[-1;2]$.
Решение: + показать
$y’=2e^{2x}-11e^x=2(e^x)^2-11e^x=2e^x(e^x-5,5).$
$y’=0$ в случае $e^x=5,5$, то есть при $x=ln5,5.$
Заметим, $0=ln1<ln5,5<lne^2=2.$
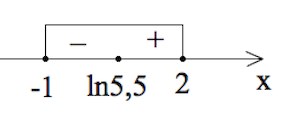
Очевидно, $x=ln5,5$ – точка минимума. В ней и будет достигаться наименьшее значение функции.
$y(ln5,5)=e^{2ln5,5}-11e^(ln5,5)-1=e^{ln5,5^2}-11\cdot 5,5-1=$ $=30,25-60,5-1=-31,25.$
Ответ: $-31,25.$
Задача 19. Найдите наибольшее значение функции $y=12\sqrt{2}cosx+12x-3\pi+9$ на отрезке $[0;\frac{\pi}{2}].$
Решение: + показать
$y’=-12\sqrt{2}sinx+12.$
$y’=0\;\Leftrightarrow \;-12\sqrt{2}sinx+12=0\;\Leftrightarrow \;sinx=\frac{\sqrt2}{2}.$
На отрезке $[0;\frac{\pi}{2}]$ мы видим следующее распределение знаков производной (для определения знака можно взять, например, значение $x=\frac{\pi}{6}$ из первого образовавшегося промежутка $[0;\frac{\pi}{4})$ и проверить знак $y'(\frac{\pi}{6})= -12\sqrt{2}sin\frac{\pi}{6}+12=6>0$):
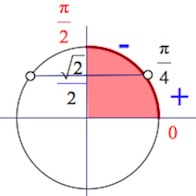
При переходе через точку экстремума ($x=\frac{\pi}{4}$) знак производной сменится.
То есть, точка $\frac{\pi}{4}$ – точка максимума. В ней и достигается наибольшее значение функции на отрезке.
$y(\frac{\pi}{4})=12\sqrt{2}cos\frac{\pi}{4}+12\cdot \frac{\pi}{4}-3\pi+9=12+3\pi-3\pi+9=21.$
Ответ: $21.$
Задача 20. Найдите наименьшее значение функции $y=-4x+2tgx+\pi+16$ на отрезке $[-\frac{\pi}{3};\frac{\pi}{3}].$
Решение: + показать
$y’=-4+\frac{2}{cos^2x}.$
$y’=0\;\Leftrightarrow \;\frac{-4cos^2x+2}{cos^2x}=0\;\Leftrightarrow \;\frac{(cosx-\frac{\sqrt2}{2})(cosx+\frac{\sqrt2}{2})}{cos^2x}=0\;\Leftrightarrow \;$
$\;\Leftrightarrow \;cosx=\pm \frac{\sqrt2}{2}.$
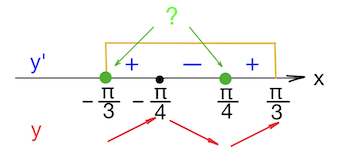
Замечаем, что функция определена на отрезке $[-\frac{\pi}{3};\frac{\pi}{3}].$ Замечаем также, что в точке $x=0$ производная функции имеет знак минус, – действительно, $y'(0)=-4+\frac{2}{cos^20}=-4+\frac{2}{1}=-2<0.$ При переходе через точки экстремума ($x=\pm \frac{\pi}{4}$) знак производной меняется.
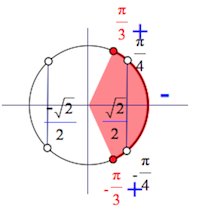
Становится видно, что $x=-\frac{\pi}{4}$ – точка максимума, точка $x=\frac{\pi}{4}$ – точка минимума.
Для нахождения наименьшего значения функции на указанном отрезке следует взять меньшее из
$y(-\frac{\pi}{3}),\;y(\frac{\pi}{4}).$
$y(-\frac{\pi}{4})=-4\cdot \frac{\pi}{4}+2tg\frac{\pi}{4}+\pi+16=18;$
$y(-\frac{\pi}{3})=-4\cdot (-\frac{\pi}{3})+2tg(-\frac{\pi}{3})+\pi+16=\frac{7\pi}{3}+16-2\sqrt3>23-2\sqrt3>18;$
$y(-\frac{\pi}{3})>y(\frac{\pi}{4}).$
То есть наименьшее значение функции на указанном отрезке – $18.$
Ответ: $18.$
Задача 21. Найдите наибольшее значение функции $y=9cosx+15x-4$ на отрезке $[-\frac{3\pi}{2};0]$ .
Решение: + показать
$y’=-9sinx+15.$
Так как
$-9\leq -9sinx\leq 9$,
то
$6\leq-9sinx+15\leq 24$.
То есть $y’>0$ при любом $x.$ Функция возрастает на $R,$ на указанном отрезке в том числе.
То есть наибольшее значение будет достигнуто в точке $0$ (правом конце отрезка).
$y(0)=9cos0+15\cdot 0-4=5.$
Ответ: $5.$
Задача 22. Найдите наименьшее значение функции $y=4cosx+\frac{15}{\pi}x+9$ на отрезке $[-\frac{2\pi}{3};0].$
Решение: + показать
$y’=-4sinx+\frac{15}{\pi}=-4(sinx+\frac{15}{4\pi}).$
Так как $\frac{15}{4\pi}<\frac{15}{4\cdot 3}=\frac{5}{4}>1,$ то $sinx+\frac{15}{4\pi}>0.$ Таким образом, $y'<0$ при любом $x.$
Функция убывает при любом $x,$ в том числе и на отрезке $[-\frac{2\pi}{3};0].$ Стало быть, достигает своего наименьшего значения на указанном отрезке в правом его конце, в точке $0.$
$y(0)=4\cdot 1+0+9=13.$
Ответ: $13.$
Задача 23. Найдите наименьшее значение функции $y=5tgx-5x+6$ на отрезке $[0;\frac{\pi}{4}].$
Решение: + показать
$y’=\frac{5}{cos^2x}-5=5(\frac{1}{cos^2x}-1)=\frac{5(1-cos^2x)}{cos^2x}=\frac{5sin^2x}{cos^2x}=5tg^2x\geq 0.$
Производная неотрицательна, на указанном отрезке в том числе, заданная функция возрастает на нем, поэтому наименьшее значение достигается функцией в левом конце отрезка, в точке $0.$
$y(0)=6.$
Ответ: $6.$
Задача 24. Найдите точку минимума функции $y=(3-2x)cosx+2sinx+19,$ принадлежащую промежутку $(0;\frac{\pi}{2})$.
Решение: + показать
$y’=(3-2x)’cosx+(3-2x)(cosx)’+(2sinx)’=-2cosx+(3-2x)(-sinx)+$
$+2cosx=(2x-3)sinx.$
На промежутке $(0;\frac{\pi}{2})$ производная имеет один ноль – в точке $\frac{3}{2}.$
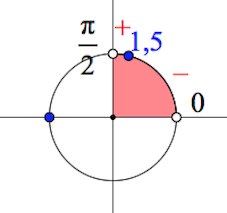
Заметим, например,
$y'(\frac{\pi}{6})=(2\cdot \frac{\pi}{6}-3)sin\frac{\pi}{6}<0$.
Становится видно, что при переходе через точку $1,5$ производная меняет знак с $-$ на $+$. Стало быть, $1,5$ – точка минимума.
Ответ: $1,5.$
Задача 25. Найдите точку минимума функции $y=(x^3-x^2+x-1)^2.$
Решение: + показать
$y’=2(x^3-x^2+x-1)(x^3-x^2+x-1)’=2(x^3-x^2+x-1)(3x^2-2x+1)=$
2(x^2(x-1)+(x-1))(3x^2-2x+1)=2(x-1)(x^2+1)(3x^2-2x+1).$
Последняя скобка произведения всегда положительна. Производная обращается в точке $x=1.$ Это и есть наша точка минимума, как несложно заметить по знакам производной при переходе через нее.
Ответ: $1.$
* Замечание. Важно!
Не следует считать (могло сложиться такое мнение при разборе примеров выше), что наименьшее (наибольшее) значение функции на отрезке совпадает с минимумом (максимумом) на отрезке!
Например, на рисунке ниже наименьшее значение функции на отрезке $[a;b]$ достигается на конце отрезка $[a;b]$, а именно, в точке $x=b$.
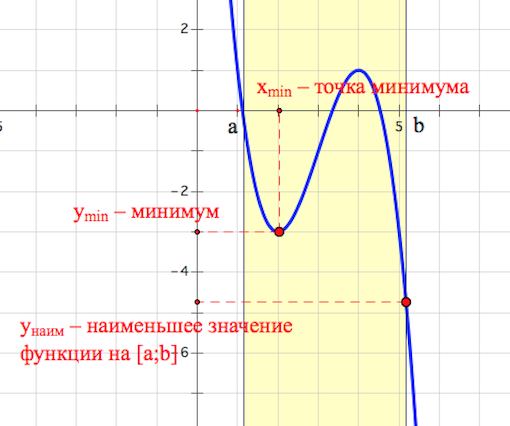
То есть, вообще говоря, при нахождении наименьшего значения функции на отрезке $[a;b]$ следует выбрать наименьшую из величин:
1) $y(x_{min})$ (их может быть несколько) из рассматриваемого отрезка $[a;b]$
2) $y(a)$, $y(b).$
При нахождении наибольшего значения функции на отрезке $[a;b]$ следует выбрать большую из величин:
1) $y(x_{max})$ (их может быть несколько) из рассматриваемого отрезка $[a;b]$
2) $y(a)$, $y(b).$
Но, если, например, на рассматриваемом отрезке функция имеет только один экстремум – минимум и мы ищем наименьшее значение, то отпадает необходимость находить значения функции на концах отрезка.
Аналогично в случае с нахождением наибольшего значения функции на отрезке, на котором содержится только один экстремум – максимум.
В случае же, когда на отрезке рассматриваемом функция не имеет экстремумов, то для нахождения наибольшего/наименьшего значений требуется лишь сравнить эти самые значения функции на концах отрезка и взять наибольшее/наименьшее из них.

Вы можете пройти тест “Исследование функции при помощи производной”














 Точка максимума – это $x=-21.$
Точка максимума – это $x=-21.$





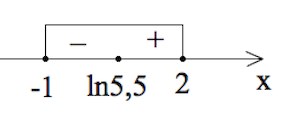




Здравствуйте,Елена Юрьевна!На одном из сайтов увидела задание:
Найдите точку минимума функции:y=(9-x)e^x+9.После преобразований производная получилась:(8-х)е^x+9.Не могли бы вы объяснить как получилось (8-х).Ведь я считала и получалось (10-х)
Это изменение как-то связано с тем что производная от (9-х)=-1?????
[latexpage]$(9-x)’=9′-x’=0-1=-1.$
[latexpage]$((9-x)e^x+9)’=((9-x)e^x)’+9’=$
$=(9-x)’e^x+(9-x)(e^x)’=-1\cdot e^x+(9-x)e^x=$
$=e^x(-1+9-x)=(8-x)e^x.$
Большое спасибо!С наступающим!
Спасибо! за подборку интересных заданий и разбор решений! Очень полезно!
:)
Нашел ошибку в задании 8.Вы нашли точку минимума, точка максимума равна 0.
Павел, ошибки нет. Я нашла именно точку максимума! Если у вас послезавтра экзамен, то вам срочно следует разобраться в этом вопросе)))
я пошел против часовой стрелки… все ясно
2 задание с ошибкой. Неправильно показано поведение функции. Даже если подставить экстремумы, получим -(((-5)^2+25)/-5)=10, -(((5)^2+25)\5)=-10 -10 5-точка минимума, а не -5 ….Ну если я сам, конечно, не накосячил ).
эм…я сам случайно стер или сайт блочит некоторые символы, имелось в виду -10 меньше 10, где -10-значение функции с аргументом x=5,а 10-значение с х=-5.
Ошибки в моих рассуждениях нет! Косяк – не мой. Ищите у себя ошибку.
Возможно, вы потеряли минус…