Теория для решения задач здесь
Задача 1. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Внешние углы», равна $0,35.$ Вероятность того, что это вопрос на тему «Вписанная окружность», равна $0,2.$ Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение:+ показать
Задача 2. При изготовлении подшипников диаметром $76$ мм вероятность того, что диаметр будет отличаться от заданного не больше чем на $0,01$ мм, равна $0,983.$ Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем $75,99$ мм или больше чем $76,01$ мм.
Решение:+ показать
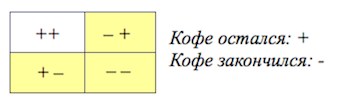
Задача 3. В тоговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна $0,3.$ Вероятность того, что кофе закончится в обоих автоматах, равна $0,16.$ Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение: + показать
Задача 4. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью $0,12$ независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение:+ показать
Задача 5. Биатлонист $5$ раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна $0,85.$ Найдите вероятность того, что биатлонист первые $3$ раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Решение: + показать
Задача 6. Вероятность того, что новый пылесос прослужит больше года, равна $0,92.$ Вероятность того, что он прослужит больше двух лет, равна $0,84.$ Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Решение: + показать
Задача 7. Вероятность того, что на тесте по математике учащийся У. верно решит больше $12$ задач, равна $0,78.$ Вероятность того, что У. верно решит больше $11$ задач, равна $0,88.$ Найдите вероятность того, что У. верно решит ровно $12$ задач.
Решение: + показать
Задача 8. Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна $0,07.$ Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение: + показать
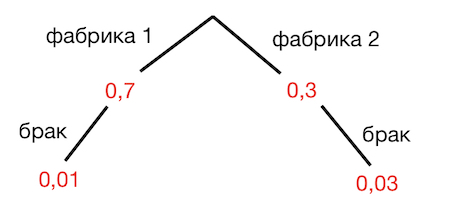
Задача 9. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает $70$% этих стекол, вторая – $30$%. Первая фабрика выпускает $1$% бракованных стекол, а вторая – $3$%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:+ показать
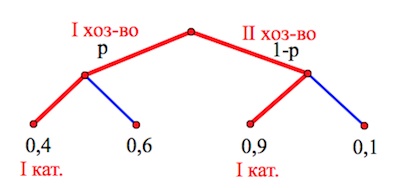
Задача 10. Агрофирма закупает куриные яйца в двух домашних хозяйствах. $40$% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — $90$% яиц высшей категории. Всего высшую категорию получает $60$% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Решение: + показать
Задача 11. Ковбой Джон попадает в муху на стене с вероятностью $0,9$, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью $0,3.$ На столе лежит $10$ револьверов, из них только $4$ пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Решение: + показать
Задача 12. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы $7$ очков в двух играх. Если команда выигрывает, она получает $6$ очков, в случае ничьей — $1$ очко, если проигрывает — $0$ очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны $0,3.$
Решение: + показать
Задача 13. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее $69$ баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее $69$ баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент А. получит не менее $69$ баллов по математике, равна $0,6$, по русскому языку — $0,6$, по иностранному языку — $0,6$ и по обществознанию — $0,9$.
Найдите вероятность того, что А. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Решение: + показать
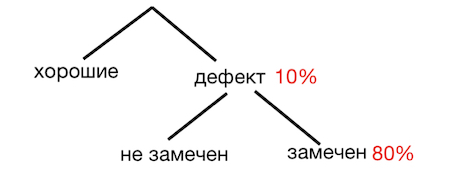
Задача 14. На фабрике керамической посуды $10$% произведённых тарелок имеют дефект. При контроле качества продукции выявляется $80$% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.
Решение: + показать
Задача 15. В кармане у Пети было $4$ монеты по рублю и $2$ монеты по два рубля. Петя, не глядя, переложил какие-то $3$ монеты в другой карман. Найдите вероятность того, что обе двухрублёвые монеты лежат в одном кармане.
Решение: + показать
Задача 16. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью $0,8$ погода завтра будет такой же, как и сегодня. 3 августа погода в Волшебной стране хорошая. Найдите вероятность того, что 6 августа в Волшебной стране будет отличная погода.
Решение: + показать
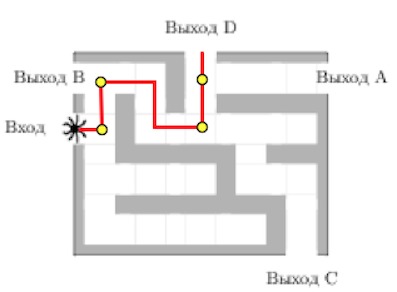
Задача 17. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D.
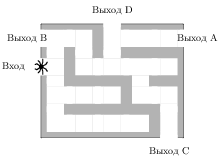
Решение: + показать
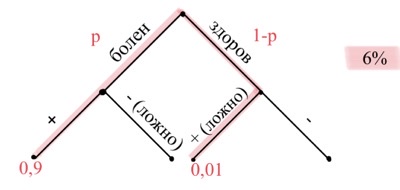
Задача 18. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ дает положительный результат с вероятностью $0,9.$ Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью $0,01.$ Известно, что у $6$% пациентов с подозрением на гепатит анализ дает положительный результат. Найдите вероятность того, что пациент, поступивший с подозрением на гепатит, действительно болен гепатитом. Ответ округлите до тысячных.
Решение: + показать
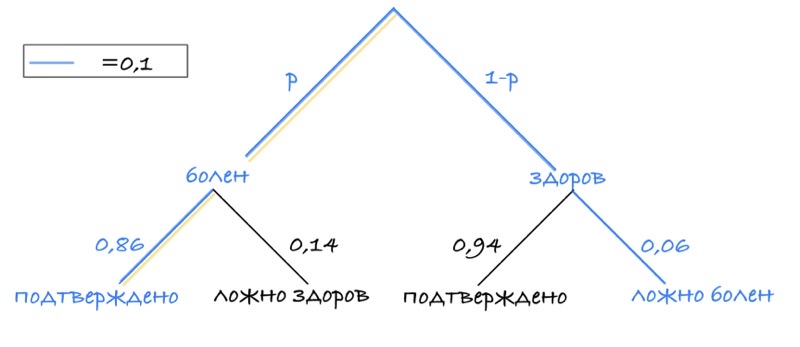
Задача 19. При подозрении на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 86% случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 94% случаев. Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование.
При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание?
Решение: + показать
Задача 20. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна $0,4$, а при каждом последующем — $0,6$. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее $0,98$?
Решение: + показать
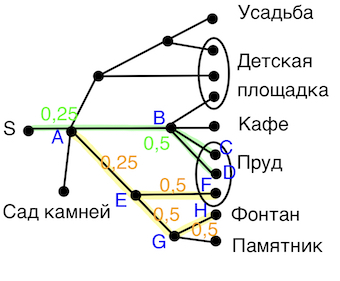
Задача 21. Артём гуляет по парку. Он выходит из точки S и, дойдя до очередной развилки, с равными шансами выбирает следующую дорожку, но не возвращается обратно. Найдите вероятность того, что таким образом он выйдет к пруду или фонтану.
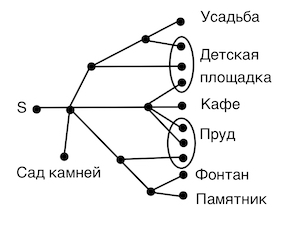
Решение: + показать
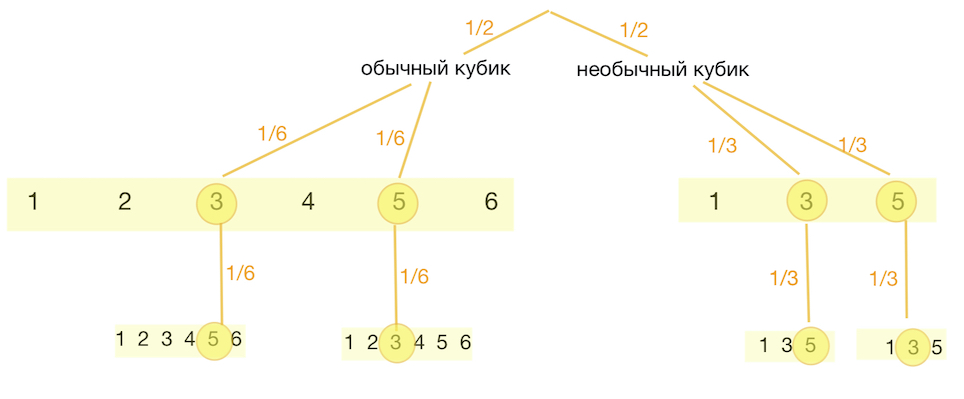
Задача 22. Первый игральный кубик обычный, а на гранях второго кубика нет чётных чисел, а нечётные числа $1$, $3$ и $5$ встречаются по два раза. В остальном кубики одинаковые.
Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали $3$ и $5$ очков. Какова вероятность того, что бросали первый кубик?
Решение: + показать
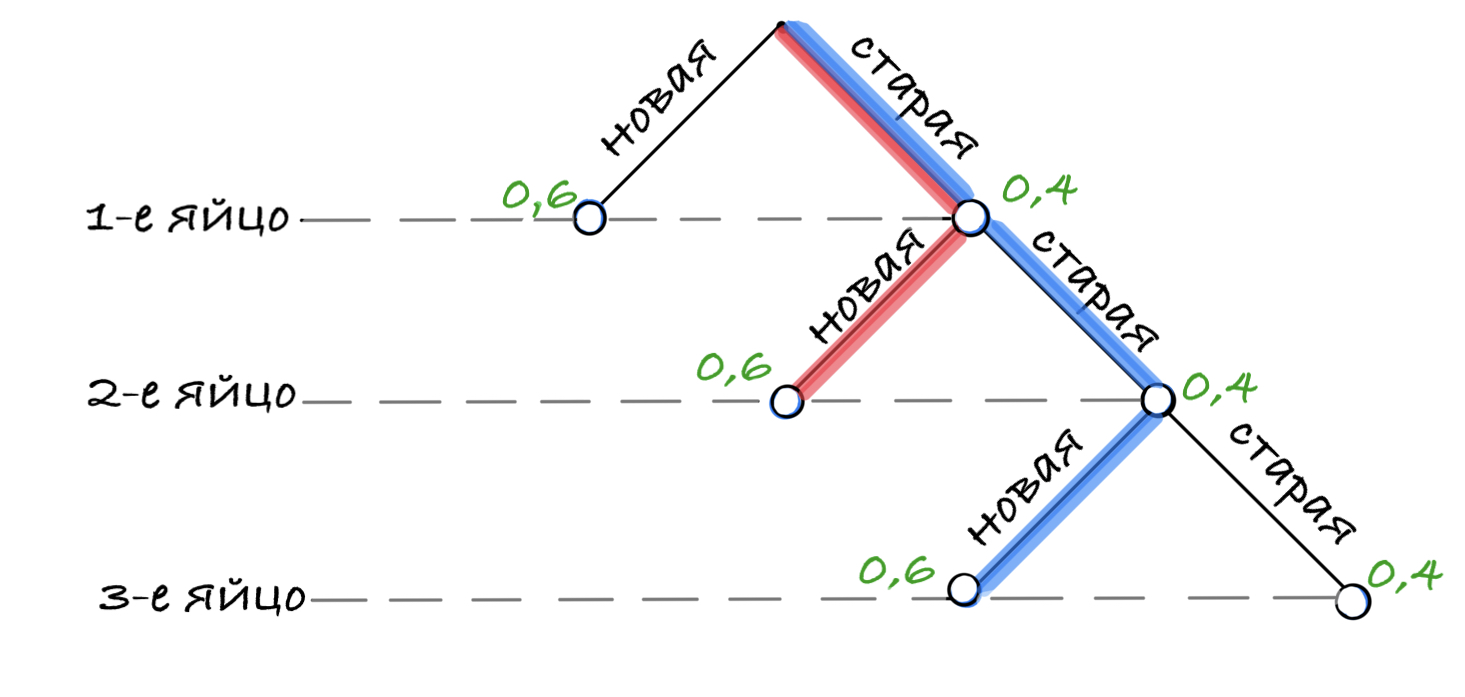
Задача 23. Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом очередном Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс.
У Маши уже есть четыре разные принцессы из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придётся купить ещё 2 или 3 шоколадных яйца?
Решение:+ показать
Задача 24. В коробке 8 синих, 6 красных и 11 зелёных фломастеров. Случайным образом выбирают два фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?
Решение: + показать
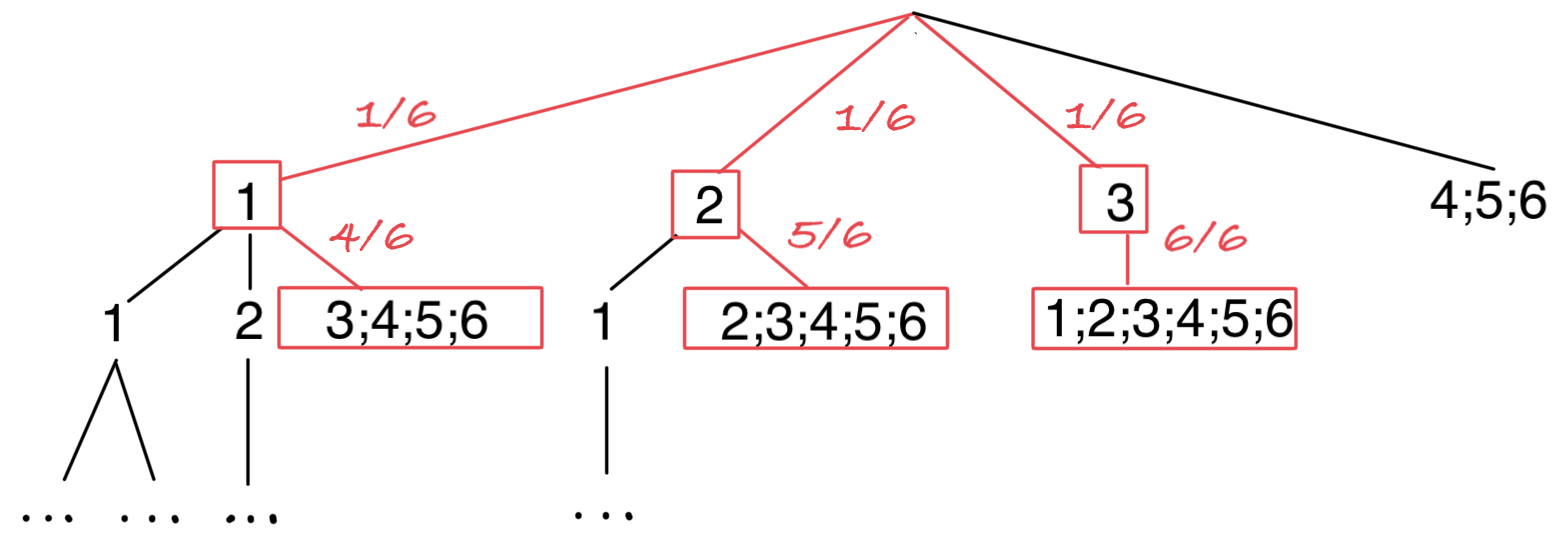
Задача 25. Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 3. Какова вероятность того, что для этого потребовалось ровно два броска? Ответ округлите до сотых.
Решение: + показать
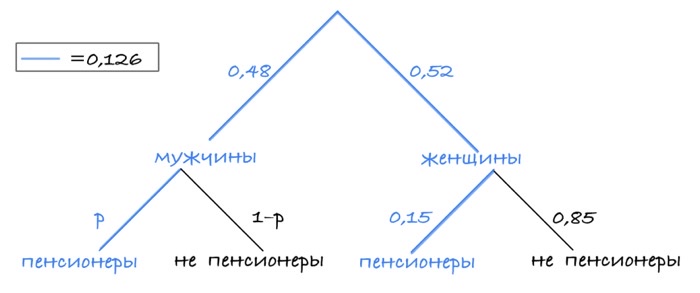
Задача 26. В городе 48 % взрослого населения — мужчины. Пенсионеры составляют 12,6 % взрослого населения, причём доля пенсионеров среди женщин равна 15 %. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».
Решение: + показать
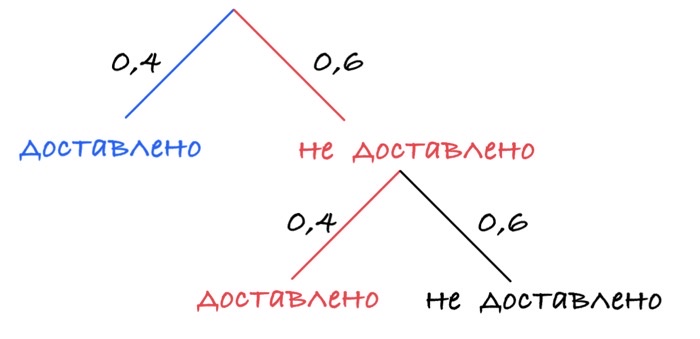
Задача 27. Телефон передаёт SMS-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой отдельной попытке, равна 0,4. Найдите вероятность того, что для передачи сообщения потребуется не больше двух попыток.
Решение: + показать
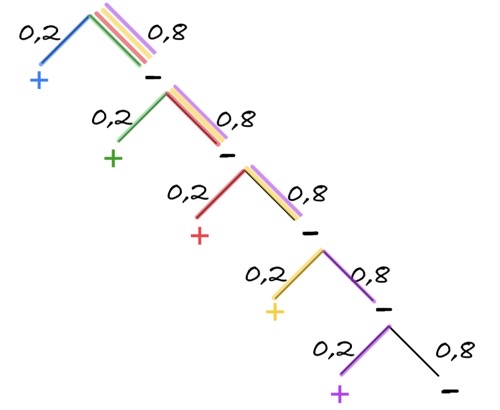
Задача 28. Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,2 при каждом отдельном выстреле. Какое наименьшее количество патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,6?
Решение: + показать
Задача 29. Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
Решение: + показать
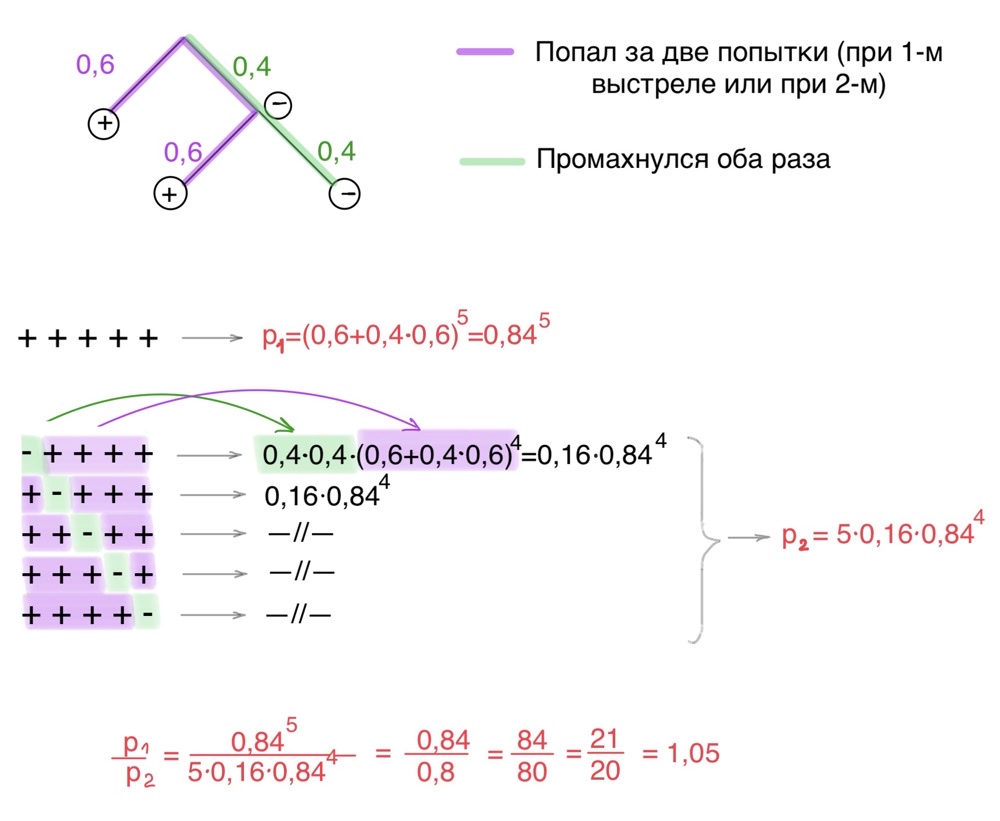
Задача 30. Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень даётся не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько раз вероятность события «стрелок поразит ровно пять мишеней» больше вероятности события «стрелок поразит ровно четыре мишени»?
Решение: + показать
Задача 31. В викторине участвуют 6 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых трёх играх победила команда А. Какова вероятность того, что эта команда выиграет четвёртый раунд?
Решение: + показать
Задача 32. Турнир по настольному теннису проводится по олимпийской системе: игроки случайным образом разбиваются на игровые пары; проигравший в каждой паре выбывает из турнира, а победитель выходит в следующий тур, где встречается со следующим противником, который определён жребием. Всего в турнире участвует 16 игроков, все они играют одинаково хорошо, поэтому в каждой встрече вероятность выигрыша и поражения у каждого игрока равна 0,5. Среди игроков два друга – Иван и Алексей. Какова вероятность того, что этим двоим в каком-то туре придётся сыграть друг с другом?
Решение: + показать
Задача 33. Игральную кость бросили два раза. Известно, что три очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 8».
Решение: + показать
Задача 34. На диаграмме Эйлера показаны события A и B в некотором случайном эксперименте, в котором 10 равновозможных элементарных событий. Элементарные события показаны точками. Найдите р(В/А) — условную вероятность события B при условии A.
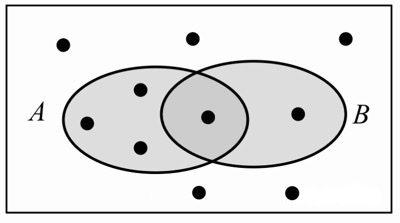
Решение: + показать
Задача 35. Для подтверждения скидки магазин отправляет покупателю на телефон сообщение с трёхзначным кодом, ровно две из цифр которого совпадают. У Пети разряжен телефон. Какова вероятность того, что он случайно угадает код? Ответ округлите до тысячных.
Решение: + показать
Задача 36. На рисунке показано дерево некоторого случайного эксперимента. Событию A благоприятствуют элементарные события a, b и c, а событию B благоприятствуют элементарные события b, c и d. Найдите P(A/B) — условную вероятность события A при условии B.
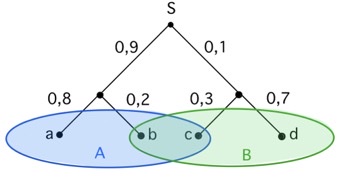
Решение: + показать

Вы можете пройти Тест


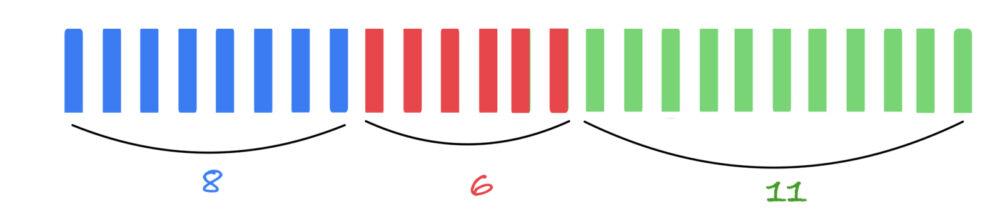 Выбираем один синий с вероятностью $\frac{8}{25}$ и один красный с вероятностью $\frac{6}{24}$.
Выбираем один синий с вероятностью $\frac{8}{25}$ и один красный с вероятностью $\frac{6}{24}$.
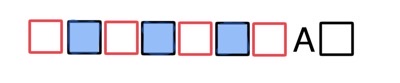 Пусть чем сильнее команда, тем она правее будет отмечена на схеме в виде квадрата. Команда А победила три другие команды (на рисунке – голубые квадраты левее А).
Пусть чем сильнее команда, тем она правее будет отмечена на схеме в виде квадрата. Команда А победила три другие команды (на рисунке – голубые квадраты левее А).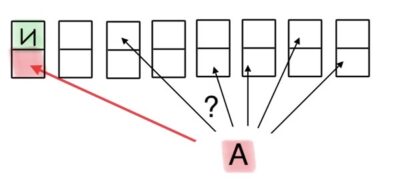
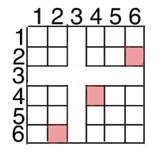 На схеме хорошо видно три благоприятных варианта из 25 возможных:
На схеме хорошо видно три благоприятных варианта из 25 возможных:
Добрый день. Помогите пожалуйста разобраться.
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде не удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша
и проигрыша одинаковы, а вероятность ничьей равна 0,1. Результат округлите до сотых.
Я так понимаю вероятность выигрыша или проигрыша равна 0,45.
Вероятность пройти в следующий круг у меня получается 0,45х0,1+0,1х0,45+0,45х0,45=0,045+0,045+0,2025=0,2925.
И это число является ответом в учебнике, но ищем-то мы вероятность непопадания. А это у меня выходит: зеркальные варианты плюс две ничьи и поражение/победа, победа/поражение. Итого 0,7075.
Опечатка в учебнике или я не прав ?
В учебниках тоже бывают ошибки…
не предать словами ,как я Вам благодарна! вы делаете великую работу!огромное спасибо))))
:)
Объясните, пожалуйста:
допустим есть два несвязанных друг с другом кофейных автомата.
для каждого вероятность того, что он исправен = 50 %.
Я правильно понимаю, что вероятность того, что хотя бы одиниз них исправен = 75%? (1-0,5*0,5).
Но тогда ведь и вероятность того, что хотя бы один НЕисправен тоже равна 75%!
Как это понимать? Значит ли это, что, скорее всего, один из них будет исправен, а другой неисправен? Если да, то как это возможно при том, что у каждого изначально шанс быть исправным и неисправным абсолютно одинаков! Спасибо.
Вы смешиваете события “один автомат исправен” и “хотя бы один исправен”. Это не одно и тоже… Не вижу противоречий…
А вы можете объяснить “человеческим языком”, что значит хотя бы один автомат будет исправен с вер. 75 % и (одновременно с этим!) хоть один будет поломан с вер. 75 %. Разве это не значит, что один скорее всего будет исправен, а другой поломан (неважно какой из них)?
Хотя бы один из двух автоматов исправен – означает:
исправен один из них и неисправен второй
или
исправен второй из них и неисправен первый
или
исправен первый и исправен второй
Аналогично с неисправностью хотя бы одного из двух автоматов.
Задача 8.
А если агрофирма купила 5 яиц у 1-го и 5.000 яиц у второго хозяйства? Как это противоречит условию задачи? Причем здесь вообще высшая категория?
Яйцо может быть высшей категории или не попадать под эту категорию. Разные сорта! Что значит “причём здесь высшая категория”?
Задание звучит: “Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.” Ни слова о том, что это яйцо должно быть высшего сорта. А если все равно, то при чем здесь высший сорт вообще?
Да, ни слова о том, что нам надо найти вероятность того, что яйцо из первого хозяйства должно быть яйцом высшего сорта.
Задание звучит: “Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.”
Но информация о яйцах высшей категории позволяет ответить на вопрос задачи. В решении это отражено.
Задча 5.
Откуда следует, что он именно первые три раза попал, а вторые два промахнулся? Может, он промахнулся-попал-промахнулся-попал-попал?
Ответ к вашему варианту – такой же. Разницы нет.
Не получается задача про монеты из теста 2. Объясните, пожалуйста.
Здравствуйте!
Объясните пожалуйста как решается такая задача.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в одном автомате закончится кофе, равна 0,6.Вероятность того, что кофе закончится в обоих автоматах, равна 0,5. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
При решении воспользовался формулой совместных событий: 0,6+0,6- -0,5=0,7 – вероятность того, что кофе закончится хотя бы в одном автомате. Тогда вероятность того, что кофе останется останется в обоих автоматах равна 1-0,7=0,3. Но с ответом не сходится. Не могу понять почему.
Ошибка в ответе
Здравствуйте. В задаче 4 у меня получается 20 исходов ,или благоприятный не нужно считать?
Есть ещё вариант 0,5*0,5*0,5*0,5. Но это запасной. Или это случайное совпадение?