Главная › ГИА › II часть › Задания II части ГИА Тренировочной работы №1 от 19 ноября 2013 г

22 Ноя 2013

Категория: II частьГИА

Задания II части ГИА Тренировочной работы №1 от 19 ноября 2013 г

Елена Репина 2013-11-22 2014-02-28

Разберем задания части 2 из Т/Р в формате ГИА.

Задание 21.

Сократить дробь $\frac{2^{n+2}\cdot 21^{n+3}}{6^{n+1}\cdot 7^{n+2}}.$

Решение:

$\frac{2^{n+2}\cdot 21^{n+3}}{6^{n+1}\cdot 7^{n+2}}=\frac{2^{n+2}\cdot (3\cdot 7)^{n+3}}{(2\cdot 3)^{n+1}\cdot 7^{n+2}}=\frac{2^{n+2}\cdot 3^{n+3}\cdot 7^{n+3}}{2^{n+1}\cdot 3^{n+1}\cdot 7^{n+2}}=$

$=2^{n+2-(n+1)}\cdot 3^{n+3-(n+1)}\cdot 7^{n+3-(n+2)}=2\cdot 3^2\cdot 7=126.$

Задание 22.

Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 130 литров она заполняет на 4 минуты быстрее, чем первая труба заполняет резервуар объемом 136 литров.

Решение:

Пусть первая труба пропускает $x$ литров воды в минуту, тогда вторая труба пропускает, согласно условию, $x+2$ литров воды в минуту.

Заполним таблицу:

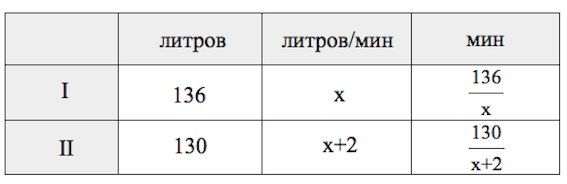
При этом $\frac{130}{x+2}$ меньше, согласно условию задачи, $\frac{136}{x}$ на 4. Тогда

$\frac{130}{x+2}+4=\frac{136}{x};$

Произведем сокращение на 2:

$\frac{65}{x+2}+2=\frac{68}{x};$

Домножаем обе части равенства на $x(x+2)$ :

$65x+2x(x+2)=68(x+2);$

$65x+2x^2+4x-68x-136=0;$

$2x^2+x-136=0;$

$D=1+4\cdot 2\cdot 136=33^2;$

$x=\frac{-1\pm 33}{4};$

$x=8$ или $x=-8,5$ (не подходит по условию);

Тогда вторая труба пропускает 10 литров в минуту.

Ответ: 10.

Задание 23.

Найдите наибольшее значение выражения $\frac{x^3-y}{x^2+1}-\frac{x^2y-x}{x^2+1}$ , если $x$ и $y$ связаны соотношением $y=x^2+x-4$ .

Решение:

Обозначим данное выражение за $A$ и подставим $y=x^2+x-4$ в $A$ :

$A=\frac{x^3-(x^2+x-4)}{x^2+1}-\frac{x^2(x^2+x-4)-x}{x^2+1}=\frac{x^3-x^2-x+4-x^4-x^3+4x^2+x}{x^2+1}=$

$=\frac{-x^4+3x^2+4}{x^2+1}=-\frac{x^4-3x^2-4}{x^2+1}.$

Дискриминант квадратного трехчлена $(x^2)^2-3x^2-4$ относительно $x^2$ равен $25$ . Заготавливаем шаблончик $x^4-3x^2-4=(x^2-...)(x^2-...)$ и действуем согласно следующему способу “превращения” суммы в произведение:

$at^2+bt+c=a(t-t_1)(t-t_2),$ где $t_1,\; t_2$ –корни $at^2+bt+c=0$

Тогда $A=-\frac{(x^2+1)(x^2-4)}{x^2+1}=-(x^2-4)=4-x^2.$

Заметим, $x^2+1\neq 0$ , поэтому $A=4-x^2$ на $R.$

Итак, нам нужно найти наибольшее значение выражения $4-x^2.$

$x^2\geq 0;$

$-x^2\leq 0;$

$4-x^2\leq 4;$

То есть $A\leq 4$ . Итак, наибольшее значение выражения $A$ – это 4.

Можно рассуждать и так: $A$ достигает своего наибольшего значения в точке – вершине параболы $A(x)=4-x^2$ , ветви которой направлены вниз. Вершина параболы $A(x)=4-x^2$ – точка $(0;4).$

Ответ: 4.

Задание 24.

В параллелограмме $ABCD$ из вершины тупого угла $B$ провели высоту $B$ к стороне $AD$ , причем $AE=ED.$ Найдите площадь параллелограмма $ABCD$ , если угол $A$ равен 60˚, а $BE=3\sqrt3.$

Решение:

Площадь $S$ параллелограмма $ABCD$ вычисляем по формуле $S=BE\cdot AD$ .

Необходимо найти $AD.$

Рассмотрим прямоугольный треугольник $ABE.$

олб

$tgA=\frac{BE}{AE};$

$tg60^{\circ}=\frac{3\sqrt3}{AE};$

$AE=\frac{3\sqrt3}{\sqrt3};$

$AE=3;$

Тогда $AD=2AE=6,$ а значит $S=3\sqrt3\cdot 6=18\sqrt3.$

Ответ: $18\sqrt3.$

Задание 25.

Окружность касается стороны $AB$ треугольника $ABC$ , у которого $\angle C=90^{\circ}$ , и продолжений его сторон $AC$ и $BC$ за точки $A$ и $B$ соответственно. Докажите, что периметр треугольника $ABC$ равен диаметру этой окружности.