Подготовка к ЕГЭ по математике

---

1. (МИОО, 2014) Дана правильная четырёхугольная пирамида $MABCD$ , рёбра основания которой равны $5\sqrt2$. Тангенс угла между прямыми $DM$ и $AL$ равен $\sqrt2$, $L$ – середина ребра $MB$. Найдите высоту данной пирамиды.

Ответ: $10.$ Решение

---

2. (Т/Р А. Ларина)  В кубе $ABCDA_1B_1C_1D_1$ точка $O_1$ – центр квадрата $ABCD$, точка $O_2$ – центр квадрата $CC_1D_1D$. а) Докажите, что прямые $A_1O_1$ и $B_1O_2$ – скрещивающиеся. б) Найдите расстояние между прямыми $A_1O_1$ и $B_1O_2$, если ребро куба равно $2$.

Ответ: $\frac{2\sqrt3}{3}.$ Решение

---

2023

---

1.1. (ЕГЭ 2023) Дана прямая призма, в основании которой лежит равнобедренная трапеция с основаниями $AD = 5$ и $BC= 4.$ $M$ – точка, которая делит сторону $A_1D_1$ в отношении $1:4,$ $K$ – середина $DD_1.$

a) Доказать, что $MCK$||$BD.$
б) Найти тангенс угла между плоскостью $MKC$ и плоскостью основания, если $\angle BAD $= 60°, a $\angle CKM$ = 90°.
Решение Ответ: $\frac{\sqrt{14}}{2}.$

1.2. (ЕГЭ 2023) Дана прямая призма, в основании которой равнобедренная трапеция с основаниями $AD = 3$ и $BC= 2.$ $M$ – точка, которая делит сторону $A_1D_1$ в отношении $1:2,$ $K$ – середина $DD_1.$

a) Доказать, что $MCK$||$BD.$
б) Найти тангенс угла между плоскостью $MKC$ и плоскостью основания, если $\angle BAD $= 60°, a $\angle CKM$ = 90°.
Ответ: $\frac{\sqrt{21}}{3}.$

---

До 2023

---

-1. (ДЕМО ЕГЭ, 2020) Все рёбра правильной треугольной призмы $ABCA_1B_1C_1$имеют длину $6$. Точки $M$ и $N$— середины рёбер $AA_1$ и $A_1C_1$ соответственно.

а) Докажите, что прямые $BM$ и $MN$ перпендикулярны.

б) Найдите угол между плоскостями $BMN$ и $ABB_1$.

 Ответ:$arcsin \frac{\sqrt 6}{4}.$ Видеорешение

---

0. (ДОСРОЧНЫЙ ЕГЭ, 2017)  Сечением прямоугольного параллелепипеда $ABCDA_1B_1C_1D_1$ плоскостью $\alpha$, содержащей прямую $BD_1$ и параллельной прямой $AC,$ является ромб.

а) Докажите, что грань $ABCD$ – квадрат.

б) Найдите угол между плоскостями $\alpha$ и $BCC_1,$ если $AA_1=6,$ $AB=4.$

 Ответ:$arctg \frac{5}{3}.$ Решение

---

1. (Т/Р А. Ларина) Ребро куба $ABCDA_1B_1C_1D_1$ равно 12. Точка $P$ – середина ребра $CB$, точка $K$ лежит на ребре $CD$ так, что $KD:KC=1:2$. Плоскость, проходящая через точки $P$, $K$ и $A_1$ пересекает ребро $DD_1$ в точке $M$.
а) Докажите, что$ DM:D_1M=1:4$.
б) Найдите угол между плоскостями $PKA_1$ и $ABC$.

Ответ: $45$. Решение

---

2. (Т/Р А. Ларина) Основанием прямой призмы $ABCA_1B_1C_1$ является равнобедренный
треугольник $ABC$, в котором $CB=CA=5$, $BA=6$. Высота призмы равна 10. Точка $M$ – середина ребра $AA_1$.
а) Постройте прямую, по которой пересекаются плоскости $MBC_1$ и $ABC$.
б) Вычислите тангенс угла между плоскостями $MBC_1$ и $ABC$.

Ответ: $\frac{5\sqrt{97}}{24}.$ Решение

---

3. (Т/Р А. Ларина) Центры вписанного и описанного шаров правильной четырехугольной пирамиды совпадают. Найдите двугранный угол при стороне основания пирамиды.

Ответ: $arccos(\sqrt2-1).$ Решение

---

4. (Т/Р А. Ларина) Основанием пирамиды является равнобокая трапеция с основаниями 18 и 8. Каждая боковая грань пирамиды наклонена к основанию под углом $60^{\circ}$.

а) Докажите, что существует точка $O$, одинаково удаленная от всех граней пирамиды (центр вписанной сферы).
б) Найдите площадь полной поверхности данной пирамиды.

Ответ: $468$. Решение

---

5. (Т/Р А. Ларина) В правильной четырехугольной пирамиде  $PABCD$ высота $PO$ равна $\sqrt7$, а сторона основания равна 6. Из точки $O$ на ребро $PC$ опущен перпендикуляр $OH$. Докажите, что прямая $PC$ перпендикулярна плоскости $BDH$. Найдите угол между плоскостями, содержащими две соседние боковые грани $PBC$ и $PCD$.

Ответ: $arccos\frac{9}{16}.$ Решение

---

6. (Т/Р А. Ларина) На боковых ребрах $AA_1$, $BB_1$ и $CC_1$ правильной треугольной призмы $ABCA_1B_1C_1$ ($AA_1|| BB_1|| CC_1$) расположены точки $K$, $L$, и $M$ соответственно. Известно, что угол между прямыми  $KL$ и $AB$ равен $\frac{\pi}{4}$, а угол между прямыми $KM$ и $AC$ – $\frac{\pi}{3}$.

а) Постройте плоскость, проходящую через точки $K$, $L$ и $M$;

б) Найдите угол между этой плоскостью и плоскостью основания $ABC.$

Ответ: $arccos\sqrt{\frac{3}{19\pm 4\sqrt3}}.$ Решение

---

7. (Т/Р А. Ларина) В основании прямой призмы $ABCDA_1B_1C_1D_1$ лежит ромб $ABCD$ со стороной $\sqrt{21}$ и углом $A$, равным 60°. На ребрах $AB,B_1C_1$ и $DC$ взяты соответственно точки $E, F$ и $G$ так, что $AE=EB$, $B_1F=FC_1$ и $DG=3GC$. Найдите косинус угла между плоскостями $EFG$ и $ABC$, если высота призмы равна $4,5$.

Ответ: $\frac{1}{\sqrt{13}}.$ Решение

---

8. (МИОО, 2013) Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD равна 108 , а площадь полной поверхности этой пирамиды равна 144. Найдите площадь сечения, проходящего через вершину S этой пирамиды и через диагональ её основания.

Ответ: $36.$ Решение

---

9. (МИОО, 2013) В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ стороны основания равны $1$ , а боковые ребра равны $5$. На ребре $AA_1$ отмечена точка $E$ так, что $AE:EA_1=2:3$. Найдите угол между плоскостями $ABC$ и $BED_1$.

Ответ: $arctg \sqrt{13}.$ Решение

---

10. (Т/Р А. Ларина) Дана правильная шестиугольная призма $ABCDEFA_1B_1C_1D_1E_1F_1$. Через точки $B,D_1, F_1$ проведена плоскость β.
а) Докажите, что плоскость β пересекает ребро $AA_1$ в такой точке $M$, что $AM:A_1M=1:2$.

б) Найдите угол, который образует плоскость β с плоскостью основания призмы, если известно, что  $AB=1, AA_1=3$.

Ответ: $arctg2.$ Решение

---

11. (Т/Р А. Ларина) В правильной треугольной пирамиде  $PABC$ ($P$ – вершина) точка $K$ – середина $AB$, точка $M$ – середина $BC$, точка $N$ лежит на ребре $AP$, причем $AN:NP=1:3$.

а) Докажите, что сечением пирамиды плоскостью, проходящей через точки $N,K,M$  является равнобедренная трапеция.
б) Найдите угол между плоскостями $NKM$ и $ABC$, если известно, что $AB=6,AP=8.$

Ответ: $arccos(\frac{15}{\sqrt{381}}).$ Решение

---

12. (Т/Р А. Ларина) В правильной четырехугольной призме $ABCDA_1B_1C_1D_1$ $AB=BC=8,AA_1=6$.

Через точки $A$ и $C$ перпендикулярно $BD_1$ проведена плоскость Ω.
а) Докажите, что плоскость Ω пересекает ребро $B_1C_1$ в такой точке $M$, что $MB_1:MC_1=7:9.$

б) Найдите угол между плоскостями Ω и $ACC_1$.

Ответ:$arctg\frac{3\sqrt2}{8}.$ Решение

---

13. (Т/Р А. Ларина) Дана прямая призма $ABCA_1B_1C_1.$

а) Докажите, что линия пересечения плоскостей $ABC_1$ и $A_1B_1C$ параллельна основаниям призмы.
б) Найдите угол между плоскостями $ABC_1$ и $A_1B_1C$, если известно, что $AC=1,BC=2,AB=\sqrt5,CC_1=3.$

Ответ: $arccos\frac{41}{49}.$ Решение 

---

1.1. (ЕГЭ 2023) В основании прямой призмы $ABCDA_1B_1C_1D_1$ лежит равнобедренная трапеция $ABCD$ с основаниями $AD=5, BC=3.$ Точка $M$ делит ребро $A_1D_1$ в отношении $A_1M:MD_1=2:3,$ а точка $K$  — середина ребра $DD_1.$

а)  Докажите, что плоскость $MKC$ делит отрезок $BB_1$ пополам.

б)  Найдите площадь сечения призмы плоскостью $MKC,$ если $\angle MKC=90^{\circ},\angle ADC=60^{\circ}.$

Решение Ответ: $\frac{12\sqrt{21}}{5}.$

1.2. (ЕГЭ 2023) В основании прямой призмы $ABCDA_1B_1C_1D_1$ лежит равнобедренная трапеция $ABCD$ с основаниями $AD=3, BC=2.$ Точка $M$ делит ребро $A_1D_1$ в отношении $A_1M:MD_1=1:2,$ а точка $K$  — середина ребра $DD_1.$

а)  Докажите, что плоскость $MKC$ делит отрезок $BB_1$ пополам.

б)  Найдите площадь сечения призмы плоскостью $MKC,$ если $\angle MKC=90^{\circ},\angle ADC=60^{\circ}.$

Ответ: $\frac{7\sqrt{10}}{6}.$

---

2.1. (ЕГЭ 2023) Основанием прямой призмы $ABCDA_1B_1C_1D_1$ является параллелограмм. На рёбрах $A_1B_1, B_1C_1,$  и $BC$ отмечены точки $M,K$ и $N$ соответственно, причем $B_1K:KC_1=1:2,$  а $AMKN$  — равнобедренная трапеция с основаниями $2$ и $3.$

a)  Докажите, что $N$  — середина $BC.$

б)  Найдите площадь трапеции $AMKN$, если объем призмы $ABCDA_1B_1C_1D_1$ равен $12,$ а ее высота равна $2.$

Решение Ответ: $\frac{5\sqrt{37}}{6}.$

2.2. (ЕГЭ 2023) Основанием прямой призмы $ABCDA_1B_1C_1D_1$ является параллелограмм. На рёбрах $A_1B_1, B_1C_1,$  и $BC$ отмечены точки $M,K$ и $N$ соответственно, причем $B_1K:KC_1=1:3,$  а $AMKN$  — равнобедренная трапеция с основаниями $3$ и $6.$

a)  Докажите, что $N$  — середина $BC.$

б)  Найдите площадь трапеции $AMKN$, если объем призмы $ABCDA_1B_1C_1D_1$ равен $24,$ а ее высота равна $3.$

Ответ: $\frac{9\sqrt{10}}{2}.$

---

3.1. (ЕГЭ 2023) Дана прямая призма ABCA₁B₁C₁.  ABC  — равнобедренный треугольник с основанием AB. На AB отмечена точка P такая, что AP : PB  =  3 : 1. Точка Q делит пополам ребро B₁C₁. Точка M делит пополам ребро BC. Через точку M проведена плоскость $\alpha$ перпендикулярная PQ.

а)  Докажите, что прямая AB параллельна плоскости α.

б)  Найдите отношение, в котором плоскость α делит отрезок PQ, если AA₁  =  5, AB  =  12 и $cos ABC=\frac{3}{5}.$ 

Решение Ответ: 16:25.

3.2. (ЕГЭ 2023) Дана прямая призма ABCA₁B₁C₁.  ABC  — равнобедренный треугольник с основанием AB. На AB отмечена точка P такая, что AP : PB  =  3 : 1. Точка Q делит пополам ребро B₁C₁. Точка M делит пополам ребро BC. Через точку M проведена плоскость $\alpha$ перпендикулярная PQ.

а)  Докажите, что прямая AB параллельна плоскости α.

б)  Найдите отношение, в котором плоскость α делит отрезок PQ, если AA₁  =  10, AB  =  20 и $cos ABC=\frac{5}{13}.$ 

Ответ: 36:25.

---

4. 1. (Досрок 2023) В четырёхугольной пирамиде $SABCD$  с основанием $ABCD$ длины всех боковых ребер равны длине ребра $AD,$ а длина каждого из рёбер  $AB,BC,CD$A ровно в два раза меньше, чем длина ребра $AD.$

а)  Докажите, что высота пирамиды проходит через середину ребра $AD.$
б)  Найдите, в каком отношении плоскость $BMN$ делит высоту пирамиды, считая от вершины $S,$ если точка $M$ — середина ребра $SD,$ а точка $N$ делит ребро $SC$ в отношении $SN:NC=3:1.$ Ответ: б)  $3 : 2.$

4.2. (Досрок 2023) В четырёхугольной пирамиде $SABCD$  с основанием $ABCD$ длины всех боковых ребер равны длине ребра $AD,$ а длина каждого из рёбер  $AB,BC,CD$A ровно в два раза меньше, чем длина ребра $AD.$

а)  Докажите, что высота пирамиды проходит через середину ребра $AD.$

б)  Найдите, в каком отношении плоскость $BMN$ делит высоту пирамиды, считая от вершины $S,$ если точка $M$ делит $SD$ в отношении $1:3,$ считая от вершины, а точка $N$ – середина ребра $SC.$

Ответ: б) $1:2.$

---

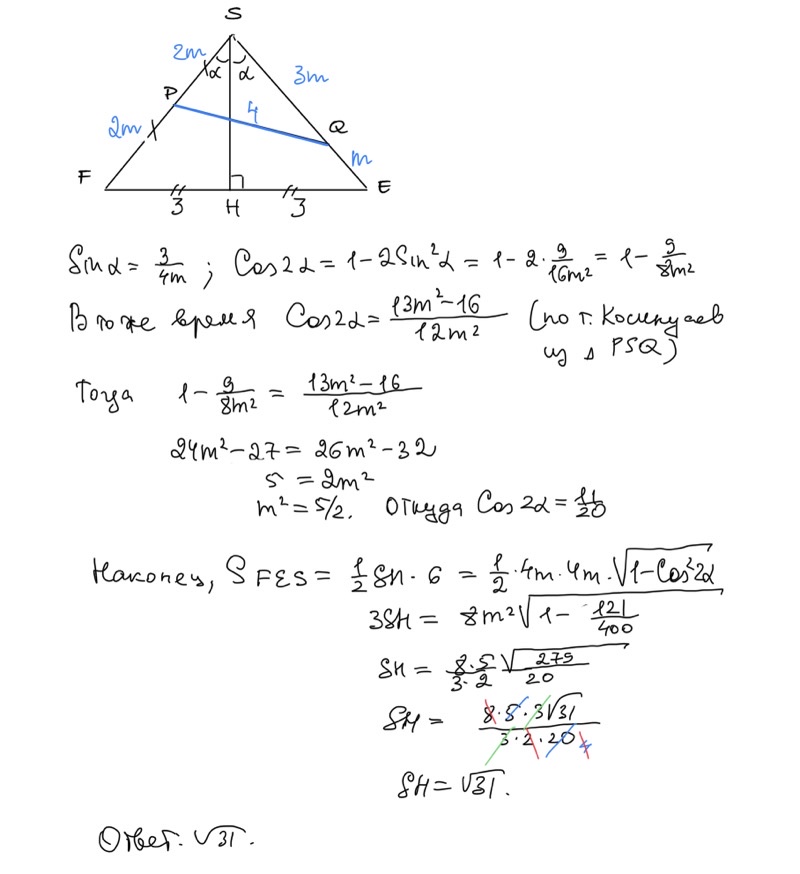
5.1. (ЕГЭ 2023, резерв) В основании четырехугольной пирамиды SABCD лежит прямоугольник ABCD. На ребрах SA, SB, SC и SD отмечены точки L, K, N и M соответственно так, что четырехугольник KLMN  — трапеция с основанием KL  =  3 и MN  =  2. Известно, что $SK:KB=3:1.$ а)  Докажите, что плоскость KLM пересекает ребра SC и SD в их серединах.
б)  Найдите высоту SH пирамиды, если точка пересечения диагоналей пирамиды совпадает с точкой H, площадь основания равна 24, а площадь сечения KLMN  =  10.

Решение Ответ: $\sqrt{31}.$

5.2. (ЕГЭ 2023, резерв) В основании четырехугольной пирамиды SABCD лежит прямоугольник ABCD. На ребрах SA, SB, SC и SD отмечены точки L, K, N и M соответственно так, что четырехугольник KLMN  — трапеция с основанием KL  =  6 и MN  =  4. Известно, что $SK:SB=3:4.$ а)  Докажите, что плоскость KLM пересекает ребра SC и SD в их серединах.  

б)  Найдите высоту SH пирамиды, если точка пересечения диагоналей пирамиды совпадает с точкой H, площадь основания равна 72, а площадь сечения KLMN  =  30.

Ответ: $\frac{3\sqrt{31}}{2}.$  

---

6.1. (ЕГЭ 2023, резерв) В основании четырехугольной пирамиды SABCD лежит квадрат ABCD. Плоскость α пересекает ребра SA, SB, SC и SD в точках L, K, N и M соответственно, причем SK : KB  =  3 : 1, а точки L и M  — середины ребер SA и SD.

а)  Докажите, что четырехугольник KLMN является трапецией, длины оснований которой относятся как 2 : 3.

б)  Найдите высоту пирамиды, если угол между плоскостями ABC и α равен 30°, площадь сечения пирамиды плоскостью α равна $10\sqrt2,$ а площадь основания пирамиды равна 32.

Решение Ответ: $8.$

6.2. (ЕГЭ 2023, резерв)  В основании четырехугольной пирамиды SABCD лежит квадрат ABCD. Плоскость α пересекает ребра SA, SB, SC и SD в точках L, K, N и M соответственно, причем SK : KB  =  2 : 1, а точки L и M  — середины ребер SA и SD.

а)  Докажите, что четырехугольник KLMN является трапецией, длины оснований которой относятся как 3 : 4.

б)  Найдите высоту пирамиды, если угол между плоскостями ABC и α равен 45°, площадь сечения пирамиды плоскостью α равна $14\sqrt3,$ а площадь основания пирамиды равна 54.
Ответ: 8.

---

7.1. (ЕГЭ 2023, резерв) Грани ABD и ACD тетраэдра ABCD являются правильными треугольниками со стороной 3 и перпендикулярны друг другу. На рёбрах и CD отмечены точки K, L и M соответственно, причём

а)  Докажите, что плоскость KLM перпендикулярна ребру CD.

б)  Найдите длину отрезка пересечения грани ABC с плоскостью KLM.
Решение Ответ: $\frac{2\sqrt6}{3}.$

7.2. (ЕГЭ 2023, резерв) Грани ABD и ACD тетраэдра ABCD являются правильными треугольниками со стороной 10 и перпендикулярны друг другу. На рёбрах AB, AD и CD отмечены точки K, L и M соответственно, причём BK  =  2, AL  =  4, MD  =  3.

а)  Докажите, что плоскость KLM перпендикулярна ребру CD.

б)  Найдите длину отрезка пересечения грани ABC и плоскости KLM.

Ответ: $\frac{\sqrt6}{3}.$

---

До 2023

---

0. (Досрочный резервн. ЕГЭ, 2018 ) Дана правильная четырехугольная призма $ABCDA_1B_1C_1D_1$. На ребре
$AA_1$ отмечена точка $K$ так, что $AK:KA_1=1:2.$ Плоскость $\alpha $ проходит через точки $B$ и $K$ параллельно прямой $AC$. Эта плоскость пересекает ребро $DD_1$ в точке $M.$
а) Докажите, что $MD:MD_1=2:1.$
б) Найдите площадь сечения, если $AB=4, AA_1=6.$ Ответ: $8\sqrt6.$  Решение

---

1. (Т/Р А. Ларина) Дана правильная четырехугольной пирамида $PABCD$ с вершиной в точке $P$. Через точку $C$ и середину ребра $AB$ перпендикулярно к основанию пирамиды проведена плоскость $\alpha$.
a) Докажите, что плоскость $\alpha$ делит ребро $BP$ в отношении $2:1$, считая от точки $B$.
б) Найдите площадь сечения пирамиды плоскостью $\alpha$, если известно, что $PA=10$, $AC=16$.

Ответ: $8\sqrt{10}.$ Решение

---

2. (Т/Р А. Ларина) В правильной треугольной призме $ABCA_1B_1C_1$ сторона основания равна 6, а боковое ребро равно 5. На ребре $CC_1$ взята точка $K$ так, что $CK:KC_1=1:4$, а на ребре $A_1C_1$ взята торчка $M$ так, что $A_1M:MC_1=1:2$.
а) Определите, в каком отношении плоскость $BKM$ делит ребро $A_1B_1$ призмы.
б) Найдите площадь сечения призмы плоскостью $BKM$.

Ответ:$\frac{19\sqrt{70}}{7}.$ Решение

---

3. (Т/Р А. Ларина) В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$   $AB=BC=8$, $BB_1=6$. Точка $K$ – середина ребра $BB_1$, точка $P$ – середина ребра $C_1D_1$. Найдите:
а) площадь сечения параллелепипеда плоскостью, проходящей через точки $K$ и $P$ параллельно прямой $BD_1$;
б) объем большей части параллелепипеда, отсекаемой от него этой плоскостью.

Ответ:а) 40;б) 336. Решение

---

4. (Т/Р А. Ларина) Сторона основания правильной четырехугольной пирамиды $SABCD$ равна 6, а высота 4. Точки $K$, $P$, $M$ – середины ребер $AB$, $BC$, $SD$.

а) Постройте сечение пирамиды плоскостью, проходящей через точки $K$, $M$, $P$.

б) Найдите площадь этого сечения.

Ответ: $6\sqrt{11}.$ Решение

---

5. (Т/Р А. Ларина) В  правильной четырехугольной пирамиде $SABCD$ длина высоты, опущенной из вершины $S$ на основание $ABCD$, равна $6\sqrt2$. Через точку касания с боковой гранью $SAB$ вписанного в эту пирамиду шара параллельно прямой $AB$ проведена плоскость, проходящая через ближайшую к вершине $S$ точку шара.
а) Постройте сечение пирамиды этой плоскостью.
б) Найдите площадь сечения, если $AB=4\sqrt6.$

Ответ: $9\sqrt3.$ Решение

---

6. (Т/Р А. Ларина) В правильной четырехугольной пирамиде $PABCD$ боковое ребро $PA=6$, а сторона основания $AB=3\sqrt2$. Через вершину $A$ перпендикулярно боковому  ребру $PC$ проведена плоскость.
а) Постройте сечение пирамиды этой плоскостью.
б) Найдите площадь полученного сечения.

Ответ: $6\sqrt3.$ Решение

---

7. (Т/Р А. Ларина) В  кубе $ABCDA_1B_1C_1D_1$ точка $K$ – середина ребра $C_1D_1$, точка $P$ – середина ребра $AD$, точка $M$ – середина ребра $CC_1$.
а) Постройте сечение куба плоскостью, проходящей через точки $K$, $P$ и $M$.
б) Найдите площадь полученного сечения, если ребро куба равно 6.

Ответ: $\frac{21\sqrt{11}}{2}.$  Решение

---

8. (Т/Р А. Ларина) Ребро куба $ABCDA_1B_1 C_1 D_1$ равно 4. Через середины ребер $AB$ и $BC$ параллельно прямой $BD_1$ проведена плоскость.
а) Постройте сечение куба этой плоскостью.
б) Найдите площадь полученного сечения.

Ответ: $7\sqrt6.$ Решение

---

9. (Т/Р А. Ларина) В кубе $ABCDA_1B_1C_1D_1$ с длиной ребра, равной 1, на вертикальном ребре $AA_1$ и на горизонтальном ребре $AB$ взяты точки $M$ и $N$ соответственно, причем $AM=\frac{1}{3},$ $AN=\frac{3}{4}$. а) Построить сечение куба плоскостью, проходящей через точки $M$ и $N$ параллельно диагонали $AC$ нижнего основания куба. б) Найти площадь этого сечения.
Ответ: $\frac{31\sqrt{133}}{288}.$ Решение

---

10. (Т/Р А. Ларина) В прямую призму $ABCDA_1B_1C_1D_1$, нижним основанием которой является ромб $ABCD$, а $AA_1$, $BB_1$, $CC_1$, $DD_1$ – боковые рёбра, вписан шар радиуса 1. а) Постройте плоскость, проходящую через вершины $A$, $B$, $C_1$. б) Найдите площадь сечения призмы этой плоскостью, если известно, что $\angle BAD=\frac{\pi}{3}.$

Ответ: $\frac{8\sqrt6}{3}$. Решение

---

11. (Т/Р А. Ларина) В основании пирамиды $SABCD$ лежит прямоугольник со сторонами  $AB=6$ и $BC=9.$ Высота пирамиды проходит через точку $O$ пересечения  диагоналей $AC$ и $BD$ основания и равна $\frac{3\sqrt3}{2}.$ Точки $E$ и $F$ лежат не ребрах $AB$ и $AD$ соответственно, причем $AE=4,\;AF=6.$ Найти площадь многоугольника, полученного при пересечении пирамиды с плоскостью, проходящей через точки $E$ и $F$ и параллельной ребру $AS.$

Ответ: $\frac{3\sqrt{183}}{2}.$ Решение

---

12. (Т/Р А. Ларина) В пирамиде $SABC$ ребра $SC$, $BC$ и $AC$ равны соответственно $\frac{\sqrt{93}}{6}$, $3$ и $4$. Известно, что угол $ABC$ тупой, ребро $SC$ перпендикулярно к плоскости основания $ABC$, а радиус окружности, описанной около треугольника $ABC$ равен $\frac{8}{\sqrt{15}}$. Найти площадь сечения пирамиды плоскостью, проходящей через вершину $S$, точку пересечения медиан треугольника $ABC$ и центр окружности, вписанной в этот треугольник.

Ответ: $\sqrt3. $ Решение

---

13. (Т/Р А. Ларина) В основании треугольной пирамиды SABC  лежит прямоугольный треугольник АВС. Середина D гипотенузы этого треугольника является основанием высоты SD данной пирамиды. Известно, что SD=2, AC=4, BC=3. Через середину высоты SD  проведено сечение пирамиды плоскостью, параллельной  ребрам AC и SB. Найти площадь этого сечения.

Ответ: $15/8.$ Решение

---

14. (ДЕМО, 2014) В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$известны ребра: $AB=3$, $AD=2$, $AA_1=5$. Точка $O$ принадлежит ребру $BB_1$  и делит его в отношении 2:3, считая от вершины $B$. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки $A$, $O$ и $C_1$.

Ответ: $\sqrt{133}.$ Решение-

15. (ЕГЭ, 2013) В правильной четырехугольной пирамиде МАВСD сторона основания равна 9/2, а боковые ребра равны 12. Найдите площадь сечения пирамиды плоскостью, проходящей через точку С и середину ребра МА параллельно прямой ВD.

Ответ:  $\frac{45\sqrt2}{4}.$ Решение

---

16. (Т/Р А. Ларина) Дана правильная шестиугольная призма $ABCDEFA_1B_1C_1D_1E_1F_1$. Через точки $B,D_1,F_1$ проведена плоскость α.
а) Докажите, что плоскость α перпендикулярна плоскости $DCC_1$.
б) Найдите площадь сечения призмы плоскостью α , если известно, что $AB=1,$ $AA_1=3$.

Ответ: $\frac{5\sqrt{15}}{4}.$ Решение

---

17. (Т/Р А. Ларина) В правильной треугольной пирамиде $PABC$ боковое ребро равно 10, а сторона основания равна $2\sqrt{30}$. Через точки $B$ и $C$ перпендикулярно ребру $PA$ проведена плоскость α.

а) Докажите, что плоскость α делит пирамиду $PABC$ на два многогранника, объемы которых относятся как $2:3$.
б) Найдите площадь сечения пирамиды $PABC$ плоскостью α.

Ответ: $18\sqrt5.$ Решение

---

18. (Т/Р А. Ларина) В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ $AB=8, BC=6, AA_1=12.$ Точка $K$ – середина ребра $AD$, точка $M$ лежит на ребре $DD_1$ так, что $DM:D_1M=1:2.$

а) Докажите, что прямая $BD_1$  параллельна плоскости $CKM$.

б) Найдите площадь сечения параллелепипеда плоскостью $CKM$.

Ответ: $2\sqrt{109}.$ Решение

---

19. (Т/Р А. Ларина) В правильной четырехугольной пирамиде $PABCD$ все ребра равны между собой. На ребре $PC$ отмечена точка $K$.

а) Докажите, что сечение пирамиды плоскостью $ABK$ является трапецией.

б) Найдите угол, который образует плоскость $ABK$ с плоскостью основания пирамиды, если известно, что $PK:KC=3:1.$

Ответ: $arctg\frac{\sqrt2}{7}.$ Решение

---

20. (Т/Р А. Ларина) Все ребра правильной шестиугольной призмы $ABCDEFA_1B_1C_1D_1E_1F_1$ равны $\sqrt{133}.$

а) Построить сечение призмы плоскостью $AFC_1$.

б) Найдите площадь этого сечения.

Ответ: $399.$ Решение

---

21. (Т/Р А. Ларина) Все рёбра куба $ABCDA_1B_1C_1D_1$ равны $\sqrt{134}$.
а) Постройте сечение куба, проходящее через середины рёбер $AB$, $BC$, $CC_1$.

б) Найдите площадь этого сечения.

Ответ: $\frac{201\sqrt3}{2}.$ Решение

---

22. (Т/Р А. Ларина) В правильной треугольной призме $ABCA_1B_1C_1$ все ребра равны между собой. Через центр верхнего основания призмы и середины двух ребер нижнего основания проведена плоскость $\beta$.
А) Найдите угол, который образует плоскость $\beta$ с плоскостью $ABC$.
Б) Найдите площадь сечения призмы $ABCA_1B_1C_1$ плоскостью $\beta$, если известно, что ребро призмы равно $6$.

Ответ: а) $arctg(4\sqrt3);$ б)$\frac{49\sqrt3}{4}.$ Решение

---

23. (ДОСРОЧНЫЙ ЕГЭ, 2016) В правильной четырехугольной призме $ABCDA_1B_1C_1D_1$ сторона основания равна $6,$ а боковое ребро $AA_1$ равно $4\sqrt3.$ На ребрах $AB,A_1D_1$ и $C_1D_1$ отмечены точки $M,N$ и $K$ соответственно, причем $AM=A_1N=C_1K=1.$

а) Пусть $L$ – точка пересечения плоскости $MNK$ с ребром $BC$. Докажите, что $MNKL$  – квадрат.

б) Найдите площадь сечения призмы плоскостью $MNK.$

Ответ: $55.$ Решение

---

24. (Т/Р А. Ларина) В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ $AB=AA_1=6, BC=4.$ Точка $P$ – середина ребра  $AB,$ точка $M$  лежит на ребре $DD_1$ так, что $DM:D_1D=2:3.$

а) Докажите, что прямая $BD_1$ параллельна плоскости $MPC.$

б) Найдите площадь сечения параллелепипеда плоскостью $MPC.$

Ответ: $3\sqrt{61}.$ Решение

---

25. (Т/Р А. Ларина) В правильной шестиугольной призме $ABCDEFA_1B_1C_1D_1E_1F_1$ на ребре $CC_1$ отмечена точка $M$ так, что $CM:C_1M=1:3$. Плоскость $AEM$ пересекает ребро $BB_1$ в точке $K$.

а) Докажите, что $BK:B_1K=1:5$.
б) Найдите площадь сечения призмы плоскостью $AEM$, если $AB=3,CC_1=8$. Ответ: $\frac{5\sqrt{291}}{4}.$ Решение

---

26. (Т/Р А. Ларина) В правильной четырехугольной пирамиде $PABCD$ сторона основания равна $20$, а высота пирамиды равна $11,25$. Через ребро $AB$ под углом $\beta $ к плоскости $ABC$ проведена плоскость α. Известно, что $tg\beta =\frac{3}{4}.$
а) Докажите, что плоскость α делит ребро $PC$ в отношении $1:4$, считая от точки $P$.

б) Найдите площадь сечения пирамиды плоскостью α. Ответ:$180.$  Решение

---

27. (Т/Р А. Ларина)  В правильной пирамиде $SABC$ ребра $AB=2$, $SC=3$. Через среднюю линию $MN$ треугольника $ABC$, параллельную $AB$, проведено сечение минимальной площади пирамиды $SABC$, пересекающее ребро $SC.$
А) Докажите, что это сечение перпендикулярно ребру $SC$.

Б) Найдите площадь этого сечения.

Ответ: $\frac{\sqrt{23}}{12}.$ Решение

---

28. (Т/Р, 2017) Точки $P$ и $Q$ — середины рёбер $AD$ и $CC_1$ куба $ABCDA_1B_1C_1D_1$ соответственно.

а) Докажите, что прямые $B_1P$ и $QB$ перпендикулярны.
б) Найдите площадь сечения куба плоскостью, проходящей через точку $P$ и

перпендикулярной прямой $BQ$, если ребро куба равно $4$.

Ответ: $8\sqrt5.$ Решение

---

28. (Т/Р А. Ларина)  Дана правильная пирамида $PABCD$ с вершиной в точке $P$. Через точку $B$ перпендикулярно прямой $DP$ проведена плоскость Ω, которая пересекает $DP$ в точке $K$.

а) Докажите, что прямые $BK$ и $AC$ перпендикулярны.
б) Найдите площадь сечения пирамиды плоскостью Ω, если известно, что сторона основания пирамиды равна $6$ и высота пирамиды равна $6$.

Ответ: $6\sqrt6.$ Решение

---

29. (Т/Р А. Ларина) В правильной пирамиде $PABCD$ на ребрах $AB$ и $PD$ взяты точки $M$ и $K$ соответственно, причем $AM:BM=1:3,DK:PK=4:3.$

а) Докажите, что прямая $BP$ параллельна плоскости $MCK$.
б) Найдите площадь сечения пирамиды плоскостью $MCK$, если известно, что все ребра пирамиды равны $4$.

Ответ:$\frac{57\sqrt{11}}{28}.$  Решение

---

30. (Т/Р 281 А. Ларина) В правильной шестиугольной призме  $ABCDEFA_1B_1C_1D_1E_1F_1$  ребро основания  $AB=2$, высота $AA_1=6$, точка $M$  – середина $F_1E_1$, проведено сечение через точки  $A$, $C$  и  $M$.

а) Докажите, что сечение проходит через середину ребра $D_1E_1.$ 

б) Найдите площадь этого сечения.

Ответ: $\frac{247\sqrt3}{20}.$ Решение 

---

2023

1.1.  (Досрок 2023) Дан тетраэдр ABCD, на ребрах AC, AD, BD, BC отмечены точки K, L, M, N соответственно так, что AK:KC=3:7, а KLMN  — квадрат со стороной 3. а)  Докажите, что BM:MD=3:7.

б)  Найдите расстояние от точки C до КLМ, если известно, что объем тетраэдра ABCD равен 50. Ответ: 4,9. Решение

1. 2.  (Досрок 2023) Дан тетраэдр ABCD. На ребре AC выбрана точка K так, что AK:KC=3:7. Также на ребрах AD, BD и BC выбраны точки L, M и N соответственно так, что KLMN  — квадрат со стороной 3.

а)  Докажите, что ребра AB и CD взаимно перпендикулярны. б)  Найдите расстояние от точки B до плоскости KLMN, если объем тетраэдра ABCD равен 100.

Ответ: $4,9.$

---

---

-4. (Реальный ЕГЭ, 2021) Дана правильная треугольная пирамида $SABC$, сторона основания $AB = 16,$ высота $SH = 10,$ точка $K$ — середина $AS.$ Плоскость, проходящая через точку $K$ и параллельная основанию пирамиды, пересекает ребра $SB$ и $SC$ в точках $Q$ и $P$ соответственно.

а) Докажите, что площадь $PQCB$ относится к площади $BSC$ как $3:4.$

б) Найдите объем пирамиды $KBQPC.$ Ответ: $80\sqrt{3}.$  Решение

---

-3. (Реальный ЕГЭ, 2017)  Основанием прямой треугольной призмы $ABCA_1B_1C_1$ является прямоугольный треугольник $ABC$ с прямым углом $C$. Диагонали боковых граней $AA_1B_1B$ и $BB_1C_1C$ равны $15$ и $9$ соответственно, $AB=13.$

а) Докажите, что треугольник $BA_1C_1$ прямоугольный.

б) Найдите объем пирамиды $AA_1C_1B.$

Ответ: $20\sqrt{14}.$ Решение

---

-2. (Реальный ЕГЭ, 2017) Дана пирамида $PABCD$, в основании которой – трапеция $ABCD$, причём $\angle BAD+\angle ADC=90^{\circ}.$ Плоскости $(PAB)$  и $(PCD)$ и  перпендикулярны плоскости основания пирамиды.

Прямые $AB$ и $CD$ пересекаются в точке $K$.

а) Доказать, что $(PAB)\perp (PCD).$

б) Найти $V_{PKBC},$ если $AB=BC=CD=3,$ а высота пирамиды равна $8.$

Ответ: $6$. Решение

---

-1. (Реальный ЕГЭ, 2017) На ребрах $AB$ и $BC$ треугольной пирамиды $ABCD$ отмечены точки $M$ и $N$ соответственно, причем $AM:MB =CN:NB=1:3$. Точки $P$ и $Q$ – середины рёбер $DA$ и $DC$ соответственно.

а) Докажите, что точки $P,Q,M$ и $N$ лежат в одной плоскости.

б) Найдите, в каком отношении эта плоскость делит объем пирамиды. Ответ: $9:23$. Решение

---

0. (Резервный ЕГЭ, 2017) В треугольной пирамиде $PABC$ с основанием $ABC$ известно, что $AB=13,PB=15,cosPBA=\frac{48}{65}.$ Основанием высоты этой пирамиды является точка $C$. Прямые $PA$ и $BC$ перпендикулярны.

а) Докажите, что треугольник $ABC$ прямоугольный.

б) Найдите объем пирамиды $PABC$.

Ответ:$90.$  Решение

---

1. (Т/Р А. Ларина) В правильной треугольной пирамиде $PABC$ ($ABC$ – основание) $M$– точка пересечения медиан грани $PBC.$

a) Докажите, что прямая $AM$ делит высоту $PO$ пирамиды в отношении $3:1$, считая от точки $P$.

б) Найдите объем многогранника с вершинами в точках $A$, $B$, $M$, $P$, если известно, что $AB=12$, $PC=10.$

Ответ: $8\sqrt{39}.$ Решение

---

2. (Т/Р А. Ларина) В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$   $AB=BC=8$, $BB_1=6.$ Точка $K$ – середина ребра $BB_1$, точка $P$ – середина ребра $C_1D_1$. Найдите:

а) площадь сечения параллелепипеда плоскостью, проходящей через точки $K$ и $P$ параллельно прямой $BD_1$;

б) объем большей части параллелепипеда, отсекаемой от него этой плоскостью.

Ответ:а) 40;б) 336. Решение

---

3. (Т/Р А. Ларина) В треугольной пирамиде два ребра, исходящие из одной вершины, равны по $\sqrt5$, а все остальные ребра равны по 2. Найдите объём пирамиды.

Ответ: $\frac{\sqrt{39}}{6}.$ Решение

---

4. (Т/Р А. Ларина) Основанием пирамиды является трапеция с основаниями 25 и 7 и острым углом arccos0,6. Каждое боковое ребро пирамиды наклонено к основанию под углом $60^{\circ}$.

а) Докажите, что существует точка M, одинаково удаленная от всех вершин пирамиды (центр описанной сферы).

б) Найдите объем данной пирамиды. Ответ: $800\sqrt3.$ Решение

---

5. (Т/Р А. Ларина) В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ известно, что $AB=8$, $BC=6$, косинус угла между прямыми $BD$ и $AC_1$ равен $0,14.$

а) Постройте сечение параллелепипеда плоскостью, проходящей через точки $B$ и $D$ параллельно прямой $AC_1$.

б) Найдите объем пирамиды, отсекаемой от параллелепипеда этой плоскостью.

Ответ: $40\sqrt3.$  Решение

---

6. (Т/Р А. Ларина) Дан прямоугольный параллелепипед  $ABCDA_1B_1C_1D_1$.

а) Постройте сечение параллелепипеда плоскостью, проходящей через точки $A$ и $C$ параллельно прямой $BD_1$.

б) Найдите отношение объемов многогранников, на которые делит параллелепипед эта плоскость.

Ответ: $11:1.$ Решение

---

7. (Т/Р А. Ларина) Плоскость пересекает боковые ребра $SA$ и $SB$ треугольной пирамиды $SABC$ в точках $K$ и $L$ соответственно и делит объем пирамиды пополам

а) Постройте сечение пирамиды плоскостью, если $SK:SA=2:3$, $SL:SB=4:5.$

б) В каком отношении эта плоскость делит медиану $SN$ грани $SBC$? Ответ: $\frac{120}{19}.$ Решение

---

8. (Т/Р А. Ларина) Сторона основания правильной четырехугольной пирамиды равна $\sqrt6$, боковое ребро составляет с высотой угол $30^{\circ}$. Плоскость $\alpha$, проходящая через вершину основания пирамиды, перпендикулярна противолежащему боковому ребру и разбивает пирамиду на две части. а) Постройте сечение пирамиды плоскостью α; б) Определите объём прилегающей к вершине части пирамиды. Ответ: $2.$ Решение

---

9. (Т/Р А. Ларина) В пирамиде $SLMN$ даны ребра $LM=5$, $MN=9$, $NL=10.$ Сфера радиуса $\frac{5\sqrt{14}}{4}$ касается плоскости основания $LMN$ и боковых ребер пирамиды. Точки касания делят  эти ребра в равных отношениях, считая от вершины $S$. Найти объем пирамиды. Ответ: $\frac{15750}{29}.$ Решение

---

10. (Т/Р А. Ларина) Дана пирамида SABC, точки D и E лежат на ребрах SA и SB, причем SD:DA=1:2 и SE:EB=1:2. Через точки D и E проведена плоскость, параллельная ребру SC. В каком отношении эта плоскость делит объем пирамиды? Ответ: $20:7. $ Решение

---

11. (Т/Р А. Ларина) На ребрах $AA_1$  и $CC_1$ куба $ABCDA_1B_1C_1D_1$ отмечены соответственно точки $E$ и $F$ такие, что $AE=2A_1E$, $CF=2C_1F$.  Через точки $B$, $E$  и $F$ проведена плоскость, делящая  куб на две части.  Найдите отношение объема части, содержащей точку $B_1$, к объему всего куба. Ответ: $25:72.$ Решение

---

12. (МГУ, 2013) Вершины $P$ и $Q$ правильного тетраэдра $MNPQ$ лежат на диагонали $A_1C$ куба $ABCDA_1B_1C_1D_1$ ($AA_1,\; BB_1,\; CC_1,\;DD_1$) с ребром единичной длины, при этом вершина $P$ лежит между $Q$ и $C$, а вершины $M$ и $N$ – на диагонали $BD$ грани $ABCD$. Найдите объем пирамиды $CMNP$. Ответ: $\frac{\sqrt6}{216}.$ Решение

---

13. (Т/Р А. Ларина) В основании пирамиды $PABCD$ лежит равнобедренная трапеция с острым углом $45^{\circ}$. Боковые грани $PAB$ и $PCD$ перпендикулярны основанию пирамиды.

a) Докажите, что плоскости $PAB$ и $PCD$ перпендикулярны.

б) Найдите площадь боковой поверхности пирамиды, если известно, что $BC=6,AD=12$, а объем пирамиды равен $27$.

Ответ:  $18(\sqrt2+\sqrt{5}).$ Решение

---

14. (Т/Р А. Ларина) Через ребро $BC$ правильной треугольной призмы $ABCA_1B_1C_1$ под углом $60^{\circ}$ к плоскости $ABC$ проведена плоскость $\alpha$. Известно, что площадь сечения призмы плоскостью $\alpha$ равна $14\sqrt3$, а высота призмы равна $3$.

а) Докажите, что плоскость $\alpha$ делит ребро $A_1B_1$ в отношении $1:3$, считая от точки $B_1$.

б) Найдите объем меньшей части, отсекаемой от призмы $ABCA_1B_1C_1$ плоскостью $\alpha$.

Ответ: $11\sqrt3$. Решение

---

15. (Т/Р А. Ларина) Треугольная призма $ABCA_1B_1C_1$ с нижним основанием $ABC$ и боковыми ребрами $AA_1,BB_1,CC_1$ рассечена плоскостью, проходящей через точки $E,F,C$, где точка $E$ является серединой ребра $AA_1$, точка $F$ лежит на ребре $BB_1$, причем $BF:FB_1=1:2.$

а) Докажите, что объем части призмы $ABCA_1B_1C_1$, заключенный между секущей плоскостью и нижним основанием этой призмы составляет $\frac{5}{18}$ объема призмы.

б) Найдите угол между нижним основанием призмы и плоскостью сечения, если призма $ABCA_1B_1C_1$ ‐ правильная и все ее ребра равны между собой.

Ответ: $arctg\frac{\sqrt{21}}{9}.$ Решение

---

16. (Т/Р А. Ларина) Основанием пирамиды $SABCD$ является трапеция $ABCD$, у которой $AD\parallel BC$. На ребре $SC$ выбрана точка $K$ так, что $CK:KS=2:5$. Плоскость, проходящая через точки $A,B$ и $K$, пересекает ребро $SD$ в точке $L$. Известно, что объемы пирамид $SABKL$ и $SABCD$ относятся, как $95:189$.

а) Постройте сечение пирамиды плоскостью $ABK$.

б) Найдите отношение длин оснований трапеции $ABCD$.

Ответ: $2.$ Решение

---

17. (СтатГрад, 2016) В одном основании прямого кругового цилиндра с высотой $12$  и радиусом основания $6$ проведена хорда $AB,$ равная радиусу основания, а в другом его основании проведен диаметр $CD,$ перпендикулярный $AB.$ Построено сечение $ABNM,$ проходящее через прямую $AB$ перпендикулярно прямой $CD$ так, что точка $C$ и центр основания цилиндра, в котором проведен диаметр $CD,$ лежат с одной стороны от сечения.

а) Докажите, что диагонали этого сечения равны между собой.

б) Найдите объем пирамиды $CABNM.$

Ответ: $144+72\sqrt3.$ Решение

---

18. (Т/Р А. Ларина) В правильной треугольной пирамиде $SABC$ сторона основания равна $6$, а боковое ребро равно $5$. На ребре $SC$ отмечена точка $M$ так, что $SM:MC=7:18.$

а) Докажите, что плоскости $SBC$ и $ABM$ перпендикулярны.

б) Найдите объем меньшей части пирамиды $SABC$, на которые ее разбивает плоскость $ABM.$ Ответ: $\frac{21\sqrt{39}}{25}.$  Решение 

---

19. (Т/Р А. Ларина) Дана правильная шестиугольная призма $ABCDEFA_1B_1C_1D_1E_1F_1$. Через точки $B$, $D_1$, $F_1$ проведена плоскость $\alpha $.

а) Докажите, что плоскость $\alpha $ пересекает ребро $CC_1$ в такой точке $M$, что $MC:MC_1=1:2.$

б) Найдите отношение объемов многогранников, на которые данную призму делит плоскость $\alpha $. Ответ: $19:35.$ Решение

---

20. (Т/Р А. Ларина) В правильной треугольной пирамиде $PABC$ боковое ребро равно $5$, а сторона основания равна $6$. На продолжении ребра $PA$ отмечена точка $M$ так, что $MA:MP=9:16.$

а) Докажите, что плоскости $PBC$ и $MBC$ перпендикулярны. б) Найдите объем пирамиды $MABC$.

Ответ: $\frac{27\sqrt{39}}{7}.$ Решение

---

21. (Т/Р А. Ларина) В правильной пирамиде $PABC$ точки $E,F,K,M,N$ – середины ребер $AC,BC,PA,PB$ и $PC$ соответственно.

а) Докажите, что объем пирамиды $NEFMK$ составляет четверть объема пирамиды $PABC$.

б) Найдите радиус сферы, проходящей через точки $N, E, F, M, K$, если известно, что $AB=8, AP=6$.

Ответ: $2,5$. Решение

---

22. (Т/Р А. Ларина) В основании приямой призмы $ABCDA_1B_1C_1D_1$ лежит трапеция $ABCD$ с основаниями $BC$ и $AD$. Точка $K$ – середина ребра $BB_1$. Плоскость $\alpha $ проходит через середины ребер $AB$ и $BB_1$ параллельно прямой $B_1D$.

А) Докажите, что сечением призмы плоскостью $\alpha $ является равнобедренная трапеция.

Б) Найдите объем большей части призмы, на которые ее разбивает плоскость $\alpha $, если известно, что $BC=7,AD=25,AB=15,BB_1=8.$ Ответ: $1416.$ Решение

---

23. (Т/Р А. Ларина) В правильной треугольной пирамиде $SABC$, точки $P$, $Q$, $R$ лежат на боковых ребрах $AS$, $CS$ и $BS$, причем $\frac{SP}{AP}=\frac{CQ}{QS}=\frac{SR}{RB}=2.$

а) Доказать, что объемы пирамид $SPRQ$ и $SABC$ относятся как $4:27$. б) Найти объем пирамиды $CPQR$, если $AB=2$ и $SA=3$. Ответ: $\frac{8\sqrt{23}}{81}.$ Решение

---

24. (Т/Р А. Ларина) В основании пирамиды $SABC$ лежит равнобедренный треугольник $ABC$, в котором $AB=4,\angle BAC=120^{\circ}$. Известно, что боковая грань $SBC$ перпендикулярна основанию $ABC$,  $SB=SC$, а высота пирамиды, проведенная из точки $S$, равна $2\sqrt{11}$ . На ребрах $SB$ и $SC$ отмечены соответственно точки $K$ и $P$ так, что $BK:SK=CP=SP=1:3.$ а) Докажите, что сечением пирамиды плоскостью $APK$ является прямоугольный треугольник.

---

25. (Т/Р А. Ларина)  В основании треугольной пирамиды $ABCD$ лежит правильный треугольник $ABC$. Боковая грань пирамиды $BCD$ перпендикулярна основанию, $BD=DC.$ а) Постройте сечение пирамиды плоскостью, проходящей через ребро $BC$ перпендикулярно ребру $AD$. б) Найдите объём пирамиды $BCPD$, где $M$ – точка пересечения ребра $AD$ и плоскости сечения, если сторона основания пирамиды $ABCD$ равна $8\sqrt3$ , а боковое ребро $AD$ наклонено к плоскости основания под углом $60^{\circ}.$ Ответ: $432.$ Решение

---

26. (Т/Р А. Ларина)  На боковых ребрах $DB$ и $DC$ треугольной пирамиды $ABCD$ расположены точки $M$ и $N$ так, что $BM=MD$ и $CN:ND=2:3.$ Через вершину $A$ основания пирамиды и точки $M$ и $N$ проведена плоскость  $\alpha,$ пересекающая медианы боковых граней, проведенных из вершины $D,$ в точках $K,R$ и $T.$ а) Докажите, что площадь треугольника $KTR$ составляет $\frac{5}{22}$ от площади сечения пирамиды плоскость $\alpha.$ б) Найти отношение объемов пирамид $KRTC$ и $ABCD.$ Ответ: $1:22.$ Решение

---

27. (Т/Р А. Ларина)   В основании пирамиды $TABCD$ лежит трапеция $ABCD,$ в которой $BC\parallel AD$ и  $AD:BC=2.$ Через вершину $T$ пирамиды проведена плоскость, параллельная прямой $BC$ и пересекающая отрезок $AB$ в точке $M$ такой, что $AM:MB=2.$ Площадь получившегося сечения равна $10,$  а расстояние от ребра $BC$ до плоскости сечения равно $4.$ а) Докажите, что плоскость сечения делит объем пирамиды в отношении $7:20.$ б) Найдите объем пирамиды. Ответ: $90.$ Решение

---

28. (Т/Р №280 А. Ларина) Плоскость $\alpha $ пендикулярна основанию правильной треугольной пирамиды  $SABC$ и делит стороны $AB$   и  $BC$   основания пополам. а) Докажите, что плоскость $\alpha $ делит боковое ребро в отношении $1:3$, считая от вершины $S$. б) Найдите отношение объемов многогранников, на которые плоскость $\alpha $ разбивает пирамиду. Ответ: $13:3$. Решение 

---

ДО 2023

---

-2. (Реальный ЕГЭ, 2021) В правильной четырехугольной пирамиде $SABCD$ сторона основания $AD=14$, высота $SH=24$. Точка $K$ — середина бокового ребра $SD$, а точка $N$ — середина ребра $CD$. Плоскость $ABK$ пересекает боковое ребро $SC$ в точке $P$.

б) Найдите расстояние от точки $P$ до плоскости $ABS$.

Ответ: $\frac{168}{25}.$ Решение

---

-1. (Реальный ЕГЭ, 2019)  В правильной треугольной пирамиде $SABC$ точка $P$ делит сторону $AB$ в отношении $2:3,$ считая от вершины $A$, точка $K$ делит сторону $BC$ в отношении $2:3,$ считая от вершины $C$. Через точки $P$ и $K$ параллельно $SB$ проведена плоскость $\gamma$. 

а) Докажите, что сечение пирамиды плоскотью $\gamma$ является прямоугольником.

б) Найдите расстояние от точки  $S$ до плоскости $\gamma$, если известно, что $SC=5,AC=6.$ 

Ответ: $\frac{9\sqrt{39}}{25}.$ Решение

---

0. (Реальный ЕГЭ, 2019) В правильной треугольной пирамиде $SABC$ точка $K$ делит сторону $SC$ в отношении $1:2$, считая от вершины $S$, точка $N$ делит сторону $SB$ в отношении $1:2$, считая от вершины $S$. Через точки $N$ и $K$ параллельно $SA$ проведена плоскость $\gamma$.

а) Докажите, что сечение пирамиды плоскотью $\gamma$ параллельно прямой $BC$.

б) Найдите расстояние от точки  $B$ до плоскости $\gamma$, если известно, что $SA=9,AB=6.$ 

Ответ: $\frac{2\sqrt{23}}{3}.$ Решение

---

1. (Т/Р А. Ларина) В правильной четырехугольной призме $ABCDA_1B_1C_1D_1$ сторона основания равна $\sqrt2$, а боковое ребро равно 2. Точка $M$ – середина ребра $AA_1$. Найдите расстояние от точки $M$ до плоскости $DA_1C_1$.

Ответ: $\frac{\sqrt5}{5}.$ Решение

---

2. (Т/Р А. Ларина) В треугольной пирамиде длины двух непересекающихся ребер равны 12 и 4, а остальные ребра имеют длину 7. В пирамиду вписана сфера. Найти расстояние от центра сферы до ребра длины 12.

Ответ: $\frac{3\sqrt{13}}{\sqrt{13}+\sqrt5}.$ Решение

---

3. (Т/Р А. Ларина) В прямоугольном параллеллепипеде $ABCDA_1B_1C_1D_1$ $AB=6,BC=4,AA_1=7.$ Точка $P$ – середина ребра $AB$, точка $M$ лежит на ребре $DD_1$ так, что $DM:D_1M=2:5.$

а) Докажите, что плоскость  $MPC$ делит объем параллелепипеда в отношении $1:11.$

б) Найдите расстояние от точки $D$ до плоскости $MPC.$

Ответ: $1\frac{11}{13}.$ Решение

---

4. (Т/Р А. Ларина) В кубе $ABCDA_1B_1C_1D_1$  точка $N$ – середина ребра $BC$, точка $M$ лежит на ребре $AB$ так, что$MB=2MA$. Плоскость, проходящая через точки $M$ и $N$ параллельно

прямой $BD_1$, пересекает ребро $DD_1$ в точке $K$.

а) Докажите, что $DK:D_1K=5:2$.

б) Найдите расстояние от точки $D_1$ до прямой $MN$, если известно, что ребро куба равно $12$.

Ответ: $12\sqrt2.$ Решение

---

5. (Т/Р А. Ларина) Все ребра правильной четырехугольной пирамиды $FABCD$ с основанием $ABCD$ равны $7$. Точки $P,Q,R$ лежат на ребрах $FA$, $AB$ и $BC$ соответственно, причем  $FP=BR=4,AQ=3.$

а) Докажите, что плоскость $PQR$ перпендикулярна ребру $FD$.

б) Найдите расстояние от вершины $D$ до плоскости $PQR.$

Ответ: $5$. Решение

---

6. (ЕГЭ, 2015) В правильной треугольной призме $ABCA_1B_1C_1$ сторона основания $AB$ равна $6$, а боковое ребро $AA_1$ равно $3$. На ребре $AB$ отмечена точка $K$ так, что $AK=1$. Точки $M$ и  $L$ – середины ребер $A_1C_1$ и $B_1C_1$ соответственно. Плоскость $\alpha $ параллельна прямой $AC$ и содержит точки $K$ и $L$.

а) Докажите, что прямая $BM$ перпендикулярна плоскости $\alpha $.

б) Найдите расстояние от точки $C$ до плоскости $\alpha .$

Ответ: $0,75. $ Решение

---

7. (ЕГЭ, 2016) В правильной треугольной призме $ABCA_1B_1C_1$ сторона основания $AB$ равна $6$, а боковое ребро $AA_1$ равно $3$. На ребре $AB$ отмечена точка $K$ так, что $AK=1$. Точки $M$ и  $L$ – середины ребер $A_1C_1$ и $B_1C_1$ соответственно. Плоскость $\alpha $ параллельна прямой $AC$ и содержит точки $K$ и $L$.

а) Докажите, что прямая $BM$ перпендикулярна плоскости $\alpha $.

б) Найдите расстояние от точки $C$ до плоскости $\alpha .$ Ответ: $0,75.$ Решение

---

8. (ЕГЭ, 2016) На ребрах $CD$ и $BB_1$ куба $ABCDA_1B_1C_1D_1$ c ребром $12$ отмечены точки $P$ и $Q$ соответственно, причем $DP=4, B_1Q=3$. Плоскость $APQ$ пересекает ребро $CC_1$ в точке $M$.
а) Докажите, что точка $M$ является серединой ребра $CC_1$.

б) Найдите расстояние от точки $C$ до плоскости $APQ$.

Ответ: $\frac{12\sqrt{26}}{13}.$ Решение

---

9. (Т/Р А. Ларина) В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ точка $M$ лежит на ребре $DD_1$ так, что $DM:D_1M=1:2.$ Плоскость, проходящая через точки $A$ и $M$ параллельно $BD_1$, пересекает ребро $CD$ в точке $P$.

а) Докажите, что $CP=DP.$

б) Найдите расстояние от точки $D_1$ до плоскости $AMP$, если известно, что  $AB=12,BC=9,AA_1=36.$

Ответ: $\frac{72}{\sqrt{61}}.$ Решение

---

10. (Т/Р А. Ларина) Дана правильная шестиугольная призма $ABCDEFA_1B_1C_1D_1E_1F_1$. На ребре $AA_1$ отмечена точка $M$ так, что $A_1M:AM=1:3$. Через точки $M$ и $B_1$ параллельно $AD_1$ проведена плоскость Ω.

а) Докажите, что плоскость Ω проходит через вершину $F_1$.

б) Найдите расстояние от точки $A$ до плоскости Ω, если $AB=2,AA_1=4.$

Ответ: $\frac{3\sqrt2}{2}.$ Решение

---

11. (Т/Р А. Ларина) В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ $AB=2,AD=1, AA_1=3.$ Точка $K$ лежит на ребре $CC_1$ так, что $CK:C_1K=5:4.$

а) Докажите, что прямые $DB_1$  и $D_1K$ перпендикулярны.

б) Найдите расстояние от точки $D_1$ до плоскости $KA_1D$.

Ответ: $\frac{18}{\sqrt{385}}.$ Решение

---

12. (Т/Р А. Ларина) В параллелепипеде $ABCDA_1B_1C_1D_1$ точка $K$ – середина ребра $AB.$

а) Докажите, что плоскость $CKD_1$ делит объем параллелепипеда в отношении $7:17$.

б) Найдите расстояние от точки $D$ до плоскости $CKD_1$, если известно, что ребра $AB,AD,AA_1$ попарно перпендикулярны и равны соответственно $6$, $4$ и $6$.

Ответ: $\frac{24}{\sqrt{41}}.$ Решение 

2024

---

1.1. (Пробник 2023) Ребро AD пирамиды DABC равно 6, а все остальные рёбра равны 5. a) Докажите, что прямые AD и ВС перпендикулярны.
б) Найдите расстояние между прямыми AD и ВС.
Решение Ответ: $\frac{\sqrt{39}}{2}.$

1.2. (Пробник 2023) Ребро AD пирамиды DABC равно 5, а все остальные рёбра равны 6. a) Докажите, что прямые AD и ВС перпендикулярны.
б) Найдите расстояние между прямыми AD и ВС.
Решение Ответ: $\frac{\sqrt{83}}{2}.$

---

2023

---

1.1. (ЕГЭ 2023) Дана четырехугольная пирамида $SABCD,$ в основании которой лежит ромб $ABCD$ со стороной $10.$ Известно, что $SA=SC=10\sqrt2,SB=20$ и $AC=10.$

а)  Докажите, что ребро $SD$ перпендикулярно плоскости основания пирамиды $ABCD.$

б)  Найдите расстояние между прямыми $AC$  и $SB.$

Решение Ответ: $2,5\sqrt3.$

1.2. (ЕГЭ 2023, аналог) Дана четырехугольная пирамида $SABCD,$ в основании которой лежит ромб $ABCD$ со стороной $5.$ Известно, что $SA=SC=5\sqrt2,SB=10$ и $AC=5.$

а)  Докажите, что ребро $SD$ перпендикулярно плоскости основания пирамиды $ABCD.$

б)  Найдите расстояние между прямыми $AC$  и $SB.$

Ответ: $\frac{5\sqrt3}{4}.$

---

0. (ЕГЭ, 2015) В правильной треугольной призме $ABCA_1B_1C_1$ все рёбра равны $2$. Точка $M$ — середина ребра $AA_1$.

а) Докажите, что прямые $MB$ и $B_1C$ перпендикулярны.

б) Найдите расстояние между прямыми $MB$ и $B_1C$.

Ответ: $\frac{\sqrt{30}}{5}.$ Решение

---

1. (Т/Р А. Ларина) В правильной шестиугольной призме $ABCDEFA_1B_1C_1D_1E_1F_1$ $AB=2,AA_1=3.$

а) Докажите, что прямые $AC_1,BE$ перпендикулярны.

б)Найдите расстояние между прямыми  $AC_1,BE$.

Ответ: $\frac{3}{\sqrt7}.$ Решение

---

2. (Т/Р А. Ларина) Ребро куба $ABCDA_1B_1C_1D_1$ равно $4$. Точка $N$ – середина ребра $CB$, а точка $M$ лежит на ребре $AA_1$, причем $AM:MA_1=3:1$. Определите расстояние между прямыми $MN$ и $BC_1$.

Ответ: $\frac{8}{\sqrt{57}}.$ Решение

---

3. (МИОО, 2013) Дана правильная треугольная призма $ABCA_1B_1C_1$, все рёбра основания которой равны $2\sqrt7$. Сечение, проходящее через боковое ребро $AA_1$ и середину $M$ ребра $B_1C_1$, является квадратом. Найдите расстояние между прямыми $A_1B$ и $AM$.

Ответ: $\frac{\sqrt6}{2}.$ Решение

---

4. (Т/Р А. Ларина) В основании прямой призмы $ABCDA_1B_1C_1D_1$ лежит ромб с диагоналями $AC=8$ и $BD=6.$

а) Докажите, что прямые $BD_1$ и $AC$ перпендикулярны.

б) Найдите расстояние между прямыми $BD_1$ и $AC$, если известно, что боковое ребро призмы равно 12.

Ответ: $\frac{6\sqrt5}{5}.$ Решение

---

5. (МГУ, 2015) В правильную треугольную призму с основаниями $ABC,A_1B_1C_1$ и ребрами $AA_1,BB_1,CC_1$ вписана сфера. Найдите ее радиус, если известно, что расстояние между прямыми $AE$ и $BD$ равно $\sqrt{13},$ где $E$ и $D$ – точки, лежащие на $A_1B_1$ и $B_1C_1$ соответственно, и $A_1E:EB_1=B_1D:DC_1=1:2.$

Ответ: $\frac{13}{6}.$ Решение

---

6. (Т/Р А. Ларина) Дана правильная шестиугольная призма $ABCDEFA_1B_1C_1D_1E_1F_1$. $O$ – точка пересечения $A_1D$ и $AD_1.$

а) Докажите, что плоскости $OB_1C_1$ и $CEE_1$ перпендикулярны.

б) Найдите расстояние между прямыми $B_1C_1$ и $CE_1$, если известно, что $AB=1,AA_1=3$.

Ответ: $1,5.$ Решение

---

7. (Т/Р А. Ларина)  Основанием пирамиды $SABC$ является равносторонний треугольник $ABC$, длина стороны которого равна $4\sqrt2$. Боковое ребро $SC$ перпендикулярно плоскости основания и имеет длину $2$.

а) Докажите, что угол между скрещивающимися прямыми, одна из которых проходит через точку $S$ и середину ребра $BC$, а другая проходит через точку $C$ и середину ребра $AB$ равен $45^{\circ}$.

б) Найдите расстояние между этими скрещивающимися прямыми. Ответ: $\frac{2\sqrt3}{3}.$ Решение

---

8. (Т/Р А. Ларина)  В правильной треугольной пирамиде $SABC$ точка $K$ – середина ребра $AB$. На ребре $SC$ взята точка $M$ так, что $SM:CM=1:3.$

а) Докажите, что прямая $MK$ пересекает высоту $SO$ пирамиды в её середине.

б) Найдите расстояние между прямыми $MK$ и $AC$, если известно, что $AB=6,SA=4.$

Ответ: $\frac{3\sqrt{21}}{7}.$ Решение Видеорешение 

---

0. (Реальный ЕГЭ, 2018)  В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки $A$ и $B$, а на окружности другого основания — точки $B_1$ и $C_1$, причем $BB_1$ — образующая цилиндра, а отрезок $AC_1$ пересекает ось цилиндра.
а) Докажите, что угол $ABC_1$ прямой.

б) Найдите угол между прямыми $BB_1$ и $AC_1$, если $AB=6, BB_1=15, B_1C_1=8.$

Ответ: $arctg \frac{2}{3}.$ Решение

---

1. (Т/Р А. Ларина) Дмитрий для тренировок купил три одинаковых футбольных мяча радиусом 12 каждый, а еще один маленький мячик ему дали в подарок. Придя домой, Дмитрий выложил все мячи на пол и неожиданно обнаружил, что когда футбольные мячи попарно касаются друг друга, то маленький мячик касается всех трех футбольных. Найдите радиус маленького мячика. Ответ: 4. Решение

---

2. (Т/Р А. Ларина) Основанием пирамиды $PABC$ является правильный треугольник $ABC$ со стороной $6$. Каждая боковая грань образует с плоскостью основания угол $\alpha=arccos0,6$. Найдите радиус сферы, вписанной в данную пирамиду.

Ответ: $\frac{\sqrt3}{2}$ или $\frac{2}{\sqrt3}.$ Решение

---

3. (Т/Р А. Ларина) Шар касается основания $ABC$ правильной треугольной пирамиды $SABC$ в точке $B$ и ее бокового ребра $SA$. Найдите радиус шара, если сторона основания пирамиды равна 3, а боковое ребро равно 4.

Ответ: $\frac{15}{2\sqrt{13}}.$ Решение

---

4. (Т/Р А. Ларина) На основании правильной треугольной пирамиды с высотой 2 лежит шар, касающийся основания в его центре. Радиус окружности, вписанной в основание, равен 1. Плоскость $p$, проведённая через вершину пирамиды и середины двух сторон основания, касается этого шара.

а) Постройте плоскость $p$;

б) Найдите радиус шара.

Ответ: $\frac{\sqrt{17}-1}{8}.$ Решение

---

5. (Т/Р А. Ларина) Известно, что $AB$, $AC$, $AD$, $DE$, $DF$ – рёбра куба. Через вершины $E$, $F$ и середины рёбер $AB$ и $AC$ проведена плоскость $\alpha$, делящая шар, вписанный в куб, на две части.

а) Постройте плоскость $\alpha$.

б) Найдите отношение объёма меньшей части шара к объёму всего шара.

Ответ: $\frac{7}{27}.$ Решение

---

6. (Т/Р А. Ларина) Сфера единичного радиуса вписана в двугранный угол величиной 60°. В тот же угол вписана сфера меньшего радиуса так, что она касается предыдущей. Угол между прямой $a$, соединяющей центры обеих сфер, и ребром двугранного угла составляет 45˚. 

а) Постройте плоскость, проходящую через ребро двугранного угла и прямую $a$.

б) Найдите радиус меньшей сферы.

Ответ: $\frac{9-4\sqrt2}{7}.$ Решение

---

7. (Т/Р А. Ларина) Длина высоты $SO$ правильной треугольной пирамиды $SABC$ равна 1, а длины сторон основания $ABC$ равны $2\sqrt6.$ Точки $M$ и $N$ – середины отрезков $AC$ и $AB$. Вычислить радиус сферы, вписанной в пирамиду $SAMN$.

Ответ: $\frac{\sqrt3}{\sqrt3+2\sqrt2+1}.$ Решение

---

8. (МИОО, 2013) В усеченный конус, образующая которого наклонена под углом 45˚ к нижнему основанию, вписан шар. Найти отношение величины боковой поверхности усеченного конуса к величине поверхности шара.

Ответ: $2.$ Решение

---

9. (ВТОРАЯ ВОЛНА ЕГЭ, 2013) В правильную шестиугольную пирамиду, боковое ребро которой равно $3\sqrt2$, а высота равна $\sqrt{10}$, вписана сфера. (Сфера касается всех граней пирамиды). Найдите площадь этой сферы.

Ответ: $120(5-2\sqrt6).$ Решение

---

10. (ДОСРОЧНЫЙ ЕГЭ, 2013) Плоскость α пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 7. Плоскость β, параллельная плоскости α, касается меньшего шара, а площадь сечения этой плоскостью большего шара равна 5. Найдите плошадь сечения большего шара плоскостью α. Ответ: $12.$  Решение

---

11. (Т/Р А. Ларина) На высоте равностороннего конуса как на диаметре построен шар.

а) Докажите, что полная поверхность конуса равновелика поверхности шара.

б) Найдите отношение объема той части конуса, которая лежит внутри шара, к объему той части шара, которая лежит вне конуса.

Ответ: $7:9.$ Решение

---

12. (Т/Р А. Ларина)  В основании пирамиды $PABC$ лежит равнобедренный треугольник $ABC$ ($AC=BC$). Все боковые ребра пирамиды попарно равны. Точка $K$ – середина $AB$. В эту пирамиду вписана сфера.

а) Докажите, что точка касания сферы с гранью $APB$ лежит на прямой $PK$.

б) Найдите радиус сферы, если известно, что $AB=6,BC=5,KP=4$.

Ответ: $\frac{15\sqrt{39}}{48+25\sqrt3}}.$ Решение

---

13. (Т/Р А. Ларина) В конусе с вершиной в точке $P$ высота равна $1$, а образующая равна $2$. В основании конуса провели диаметр $CD$ и перпендикулярную ему хорду $AB$. Известно, что хорда $AB$ удалена от центра основания на расстояние, равное $1$.

а) Докажите, что треугольник $PAB$ прямоугольный.

б) Найдите сумму объемов пирамид $CAPB$ и $DAPB$.

Ответ: $\frac{2\sqrt6}{3}.$ Решение

---

14. (Т/Р А. Ларина)  Внутри куба расположены два равных шара, касающихся друга. При этом один шар касается трех граней куба, имеющих общую вершину, а другой касается трех оставшихся граней.

а) Докажите, что центры шаров принадлежат диагонали куба, исходящей из общей для граней вершины.

б) Найдите радиусы этих шаров, если ребро куба равно  $13$.

Ответ: $\frac{13\sqrt3}{2\sqrt2+2}.$ Решение

---

1. (Т/Р А. Ларина) В правильной четырехугольной пирамиде $PABCD$ высота $PO$ в полтора раза больше, чем сторона основания.
а) Докажите, что через точку $O$ можно провести такой отрезок $KM$ с концами на сторонах $AD$ и $BC$ соответственно, что сечение $PKM$ пирамиды будет равновелико основанию пирамиды. 

б) Найдите отношение площади полной поверхности пирамиды $PABMK$ к площади полной поверхности пирамиды $PABCD$.

Ответ: $\frac{7+2\sqrt{10}}{18}.$ Решение

---

2. (Т/Р А. Ларина) На ребрах $AA_1$, $CC_1$, $C_1D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$ расположены точки $M,N$ и $P$ так, что $AM:AA_1=C_1N:C_1C=C_1P:C_1D_1=4:5$.

а) Постройте точку $H$ пересечения плоскости $MNP$ с прямой $BC$.

б) Найдите отношение $BH:BC.$

Ответ:  $1:2.$ Решение