Архив по категории: 03 Стереометрия
13
Сен 2013
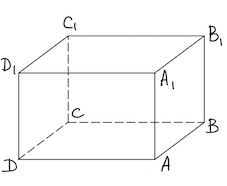
02. Куб. Параллелепипед
Елена Репина 2013-09-13 2024-01-17Автор: |
комментариев 19
12
Сен 2013
02. Призма
Елена Репина 2013-09-12 2023-08-03Автор: |
комментариев 13
11
Сен 2013
02. Пирамида
Елена Репина 2013-09-11 2023-08-03Автор: |
комментарий 21
10
Сен 2013
02. Цилиндр.
Елена Репина 2013-09-10 2023-08-03Автор: |
комментария 3
09
Сен 2013
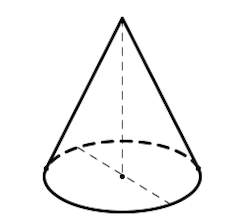
02. Конус
Елена Репина 2013-09-09 2023-08-03Автор: |
комментариев 10
08
Сен 2013
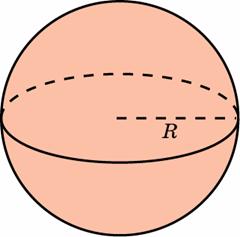
02. Шар
Елена Репина 2013-09-08 2023-08-03Автор: |
комментариев 7
07
Сен 2013
02. Составные многогранники. Углы и расстояния
Елена Репина 2013-09-07 2023-08-03Автор: |
Нет комментариев
07
Сен 2013
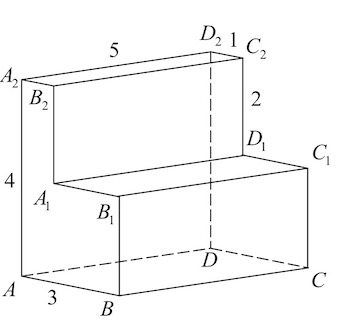
02. Составные многогранники. Площадь поверхности. Объем
Елена Репина 2013-09-07 2023-08-03Автор: |
комментариев 14
06
Июл 2013
02. Комбинации тел
Елена Репина 2013-07-06 2023-08-07Автор: |
Нет комментариев