!! Смотрите также ПОДБОРКУ ЗАДАЧ №18 (с ответами) для подготовки к ЕГЭ !!
Системы с параметром + показать
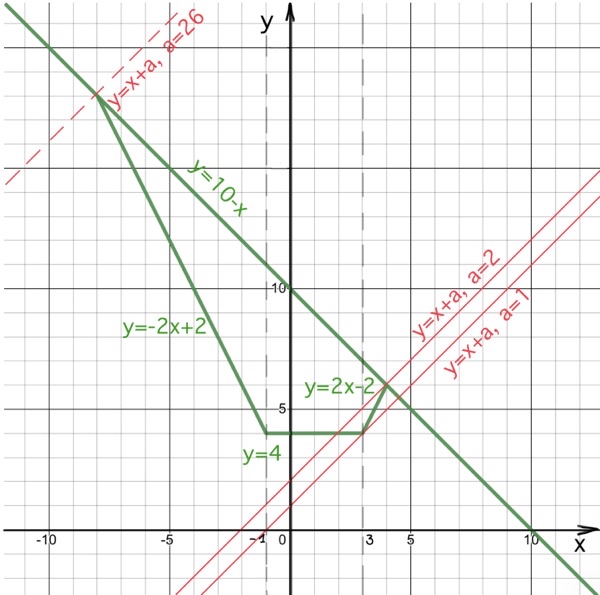
2023 1.1. (ЕГЭ 2023) Найдите все значения параметра a, при каждом из которых $\begin{cases}(x^2+y^2+4x)\sqrt{2x+y+6}=0,\\y=a(x-2)&\end{cases}$ система уравнений имеет 2 различных решения. Решение Ответ: $[-\frac{3}{14};\frac{1}{2}]\cup ${$\pm \frac{1}{\sqrt3}$}. 1.2. (ЕГЭ 2023) Найдите все значения параметра a, при каждом из которых $\begin{cases}(x^2+y^2+6x)\sqrt{x+y+6}=0,\\y=x+a&\end{cases}$ система уравнений имеет 2 различных решения. Ответ: $[0;6]\cup${$3\pm3\sqrt2$}. $\begin{cases}x^2+x+|x^2-x-2|=y^2+y+|y^2-y-2|,\\x+y=a\end{cases}$ система уравнений имеет более двух решений. Решение Ответ: $(-2;0]$ 2.2. (ЕГЭ 2023, резерв) Найдите все значения параметра a, при каждом из которых $\begin{cases}|x^2-1|-2x-x^2=|y^2-1|-2y-y^2,\\x+y=a\end{cases}$ система уравнений имеет более двух решений. Ответ: $(-2;-1]$ 3.1. (ЕГЭ 2023) Найдите все значения параметра a, при каждом из которых $\begin{cases}(|x+1|+|x-3|-y)\sqrt{10-x-y}=0,\\y=x+a;&\end{cases}$ система уравнений имеет 2 различных решения. Решение Ответ: {$1$}$\cup[2;26).$ 3.2. (ЕГЭ 2023) Найдите все значения параметра a, при каждом из которых $\begin{cases}(|x+2|+|x-1|-y)\sqrt{10-x-y}=0,\\y=x+a;&\end{cases}$ система уравнений имеет 2 различных решения. Ответ: {$2$}$\cup[4;32).$ до 2023 -5. (ДЕМО ЕГЭ, 2020) Найдите все положительные значения параметра a, при каждом из которых система уравнений $\begin{cases} имеет ровно одно решения. Ответ: $2;\sqrt{65}+3.$ Видеорешение -4. (Реальный ЕГЭ, 2018) Найдите все значения параметра a, при каждом из которых система $\begin{cases} имеет ровно четыре решения. Ответ: $(\frac{-2-\sqrt2}{3};-1)\cup (-1;-0,6)\cup (-0,6;-2+\sqrt2).$ Решение -3. (Досрочный резервный ЕГЭ, 2018) Найдите все значения параметра a, при каждом из которых система уравнений $\begin{cases} имеет ровно два различных решения. Ответ: $(1;2]\cup [8;9).$ Решение -2. (Досрочный ЕГЭ, 2018) Найдите все значения параметра $a$, при каждом из которых система уравнений $\begin{cases} имеет ровно два различных решения? Ответ: $2;6.$ Решение -1. (Резервный ЕГЭ, 2017) Найдите все значения $a$, при каждом из которых система уравнений $\begin{cases}(y^2-xy+x-3y+2)\sqrt{x+3}=0,\\a-x-y=0;&\end{cases}$ имеет ровно два различных решения. Ответ: $(-4;-2]\cup ${$0$}. Решение 0. (Досрочный, 2017) Найдите все значения параметра $a$, при каждом из которых система неравенств $\begin{cases}ax\geq 2,\\\sqrt{x-1}>a,\\3x\leq 2a+11;&\end{cases}$ имеет хотя бы одно решение на отрезке $[3;4].$ Ответ: $[0,5;\sqrt3).$ Решение 1. (Досрочный, 2016) Найдите все значения параметра $a,$ при каждом из которых система уравнений $\begin{cases}\frac{xy^2-3xy-3y+9}{\sqrt{x+3}}=0,\\y=ax;&\end{cases}$ имеет ровно два различных решения. Ответ: $(0;\frac{1}{3}]\cup ${$3$} Решение 2. (Т/Р, 2016) Найдите все неотрицательные значения $a$, при каждом из которых система уравнений $\begin{cases}\sqrt{(x+2)^2+y^2}+\sqrt{x^2+(y-a)^2}=\sqrt{4+a^2},\\5y=|6-a^2|;&\end{cases}$ имеет единственное решение. Ответ: $[1;6].$ Решение 3. (ЕГЭ, 2016) Определите, при каких значениях параметра система уравнений $\begin{cases}x(x^2+y^2+y-2)=|x|(y+2),\\y=x+a;&\end{cases}$ имеет ровно три различных решения. Ответ: $(-2\sqrt2;-2)\cup (-2;0]\cup${$-1+\sqrt2$}. Решение 4. (ЕГЭ, 2016, резерв) Найдите все значения параметра $a$, при каждом из которых система уравнений $\begin{cases}(x-3)(y+3x-9)=|x-3|^3,\\y=x+a;&\end{cases}$ имеет ровно четыре решения. Ответ: $(-7;-3)\cup (-3;1).$ Решение 5. (Т/Р Ларина) Найдите все значения $a$, при которых система $\begin{cases}|x^2-x-6|=(y-1)^2+x-7,\\3y=2x+a;&\end{cases}$ имеет ровно один или два корня. Ответ: $(-\infty;-10)\cup(-9;-2]\cup[3;+\infty).$ Решение 6. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых система уравнений $\begin{cases}2cosx+asiny=1,\\log_zsiny=(log_za)\cdot log_a(2-3cosx),\\log_az+log_a(\frac{1}{2a}-1)=0;&\end{cases}$ имеет хотя бы одно решение. Ответ: $(0;\frac{1}{4})\cup (\frac{1}{4};\frac{1}{3}].$ Решение 7. (Т/Р Ларина) Найдите все значения параметра $b$, при которых система $\begin{cases}cos(y-b)-2cosx=0,\\log_2(by-y^2)=2log_4(-x)-log_{\frac{1}{2}}(3y);&\end{cases}$ имеет нечетное число решений. Ответ: $(\frac{3\pi}{2}+6\pi n;\frac{9\pi}{2}+6\pi n],n\in Z.$ Решение 8. (Т/Р Ларина) При каких значениях параметра $a$ система уравнений $\begin{cases}2|x-a+3|+|2y+a|=4,\\(x-y+3)(x-y+6)=0;&\end{cases}$ имеет ровно два решения? Ответ: $(-\frac{10}{3};-\frac{4}{3})\cup (-\frac{2}{3};\frac{4}{3}).$ Решение 9. (Т/Р Ларина) Найдите все значения параметра $a$, прри каждом из которых система уравнений $\begin{cases}\sqrt{x^2+y^2+3(3-2|x|)}+\sqrt{y^2+y-a+8(2-|y|)}=5,\\y-x^2=a;&\end{cases}$ имеет ровно четыре решения. Ответ:$(-9;-4)\cup ${$-\frac{32}{9}$}. Решение 10. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых система $\begin{cases}\sqrt{(x-4)^2+y^2}+\sqrt{(x-4)^2+(y-4)^2}=4,\\(x-a)^2+(y-a)^2=4;&\end{cases}$ имеет ровно одно решение. Ответ: {$2$}$\cup (4-\sqrt2;4+\sqrt2].$ Решение 11. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых система уравнений $\begin{cases}\frac{x^2+y^2+8x-6y+21}{\sqrt{y-x-5}}=0,\\y=a(x-1)+3;&\end{cases}$ имеет ровно одно решение. Ответ:{$-\frac{2\sqrt{21}}{21}$}$\cup [0;\frac{2}{5}).$ Решение 12. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых система $\begin{cases}(x+3)^2+(|y|-7)^2=9,\\(x-9)^2+(y-2)^2=a;&\end{cases}$ имеет ровно три решения. Ответ: $144;256.$ Решение 13. (ЕГЭ, 2015) Найдите все значения параметра $a$, при каждом из которых система уравнений $\begin{cases}x^2-8x+y^2+4y+15=4|2x-y-10|,\\x+2y=a;&\end{cases}$ имеет более двух решений. Ответ: $(-5\sqrt5;-5]\cup [5;5\sqrt5).$ Решение 14. (Т/Р Ларина) Найдите все значения параметра а, при каждом из которых система уравнений $\begin{cases}\sqrt{y^2+y-20|y|-6x-a+113}+\sqrt{y^2+y+12|y|+10x-a+49}=\sqrt{320},\\x^2-2x-y+a+3=0;&\end{cases}$ имее ровно два решения. Ответ: {$-6;-5$}$\cup [-1;3)$. Решение 15. (Т/Р Ларина)Найдите все значения параметра а, при каждом из которых система $\begin{cases}(y-2a+2)^2+(x-a)^2}=a^2-5a+4,\\y\geq |x|;&\end{cases}$ имеет единственное решение. Ответ: $0;4;3-\sqrt5.$ Решение 16. (Т/Р Ларина) Найдите все значения параметра а, при каждом из которых система $\begin{cases}x(xy-x^2+6x-9)=y(2x+y+3),\\4(y-ax)=3(4a-3);&\end{cases}$ имеет ровно два решения. Ответ: $-18;0;\frac{1}{16};\frac{3}{8};1.$ Решение 17. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых система $\begin{cases}\frac{(y^2+x^2-1)(y^2-y+x^2-x)}{\sqrt{y-x}}=0,\\y+x=a;&\end{cases}$ имеет ровно одно решение. Ответ: $(-\sqrt2;0]\cup ${$1$}$\cup [\sqrt2;2).$ Решение 18. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых система $\begin{cases}\frac{y^3+yx^2-4y}{\sqrt{x+1}}=0,\\y-ax=5a+2;&\end{cases}$ имеет ровно одно решение. Ответ: $(-\frac{\sqrt3+2}{4};-\frac{1}{2}]\cup${$-\frac{2}{7};0$}. Решение 19. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых множество решений системы $\begin{cases}x^2+(a+4)x+4a\leq y,\\3x+y-(2a+4)\leq 0;&\end{cases}$ содержит отрезок $AB$, где $A(-2;0),$ $B(-1;0).$ Ответ: $[-3,5;1].$ Решение 20. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых система уравнений $\begin{cases}x+\sqrt y=1,\\a+3-\sqrt y=\frac{1}{2}(a-x)^2;&\end{cases}$ имеет единственное решение. Ответ: {$-\frac{5}{4}$}$\cup (-1;5].$ Решение 21. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых система $\begin{cases}a^2+ax-2x-4a+4\leq 0,\\xa=-4;&\end{cases}$ имеет хотя бы одно решение. Ответ: $[1-\sqrt5;0)\cup [2;1+\sqrt5].$ Решение 21. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых система $\begin{cases}a^2-x^2+2x-2a\leq 0,\\x^2=4x-a;&\end{cases}$ имеет ровно одно решение. Ответ: $[\frac{-1-\sqrt{17}}{2};0)\cup (\frac{-1+\sqrt{17}}{2};3].$ Решение 22. (Т/Р Ларина) При каком наибольшем значении параметра $a$ система уравнений имеет единственное решение $\begin{cases}(x+a\sqrt3)^2+y^2+6y+8=0,\\\sqrt3|x|+y=6;&\end{cases}$ Ответ: $\frac{11}{3}.$ Решение 23. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых система $\begin{cases}\sqrt{x^2+2x+y^2-4y+5}+\sqrt{x^2-4x+y^2-12y+40}=5,\\y=x^2+a;&\end{cases}$ имеет ровно два решения. Ответ: $[2;\frac{34}{9}).$ Решение 24. (Т/Р Ларина) Найдите все значения параметра а, при которых система уравнений $\begin{cases}y=\frac{(x-1)^2}{2},\\lg(5-a-y)=lg(a-x);&\end{cases}$ имеет решение. Ответ: $(-3;3,25].$ Решение 25. (Т/Р Ларина) При каких значениях параметра $a$ система уравнений $\begin{cases}y^2+2xy+(x^2+2x-3)(3-x^2)=0,\\y-ax-6a=0;&\end{cases}$ имеет более двух различных решений? Ответ: $(-\infty;-12-2\sqrt{33}]\cup [-12+2\sqrt{33};10-2\sqrt{21}]\cup [10+2\sqrt{21};+\infty].$ Решение 26. (Т/Р Ларина) Найдите все значения а, при каждом из которых система неравенств $\begin{cases}x^2+y^2-a^2\leq 6x-4y-13,\\x^2+y^2-4a^2\leq 8y-10x+4a-40;&\end{cases}$ имеет ровно одно решение. Ответ:$-\frac{11}{3};3.$ Решение 27. (Т/Р Ларина) Найдите все значения параметра а, при каждом из которых система $\begin{cases}y^2+xy-7x-14y+49=0,\\y=ax^2+1,\\x\geq 3;&\end{cases}$ имеет ровно одно решение. Ответ: {$-\frac{1}{24};0$}$(\frac{1}{3};\frac{2}{3}].$ Решение 27. (ЕГЭ, 2013) При каких действительных значениях параметра a система $\begin{cases}3|x|+2|y|=12\\y=ax^2+1,\\x^2 +y^2=a^2;&\end{cases}$ имеет наибольшее число решений? Ответ: $(-4;-\frac{12}{\sqrt{13}})\cup (\frac{12}{\sqrt{13};4}).$ Решение 28. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых система уравнений $\begin{cases}cos(cosx)-cosy=(a^2+1)(y-cosx),\\2y^2-(3a-8)cosx+a^2-4a=0;&\end{cases}$ не имеет решений. Ответ: $(-\infty;-2)\cup (2;3)\cup (5;+\infty)$. Решение 29. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых система $\begin{cases}\sqrt{(x-3)^2+(y-2)^2}+\sqrt{(x-6)^2+(y-2)^2}=3,\\(x-a)^2+(y+2a-8)^2=a-3;&\end{cases}$ имеет ровно одно решение. Ответ: $[3;3,2)\cup${$3,25$}. Решение 30. (Т/Р Ларина) Найти все $a$, при каждом из которых система $\begin{cases}y-ax=a+5,\\xy^2-x^2y-2xy+4x-4y+8=0;&\end{cases}$ имеет ровно два решения. Ответ: ${-25; \pm 1;0;1\pm \frac{4}{\sqrt5}}.$ Решение 31. (Т/Р Ларина) При каких значениях параметра $a$ система уравнений $\begin{cases} имеет единственное решение? Ответ: $ (-0,8;1]\cup \left \{ 4 \right \}.$ Решение 32. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых система $\begin{cases} имеет ровно два решения? Ответ: $-\frac{1}{24};0;1$. Решение 33. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых уравнение $\begin{cases} имеет ровно два решения. Ответ: {$-\sqrt{2+2\sqrt2}$}$\cup(-2;2)\cup${$ \sqrt{2+2\sqrt2}$}. Решение 34. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых существует хотя бы одно $x,$ удовлетворяющее условию: $\begin{cases}x^2+(5a+2)x+4a^2+2a<0,\\x^2+a^2=4;&\end{cases}$ Ответ: $(-\sqrt2;-\frac{16}{17})\cup (0;\sqrt2).$ Решение 35. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых существует хотя бы одно $x,$ удовлетворяющее условию: $\begin{cases}|x^2-5x+4|-9x^2-5x+4+10x|x|=0,\\x^2-2(a-1)x+a(a-2)=0;&\end{cases}$ Ответ: {$-1$}$\cup[1;6].$ Решение
2.1. (ЕГЭ 2023, резерв) Найдите все значения параметра a, при каждом из которых
(|x|-5)^2+(y-4)^2=9,\\ (x+2)^2+y^2=a^2;
\end{cases}$
уравнений
x^2+y^2-4(a+1)x-2ay+5a^2+8a+3=0,\\ x^2=y^2;
\end{cases}$
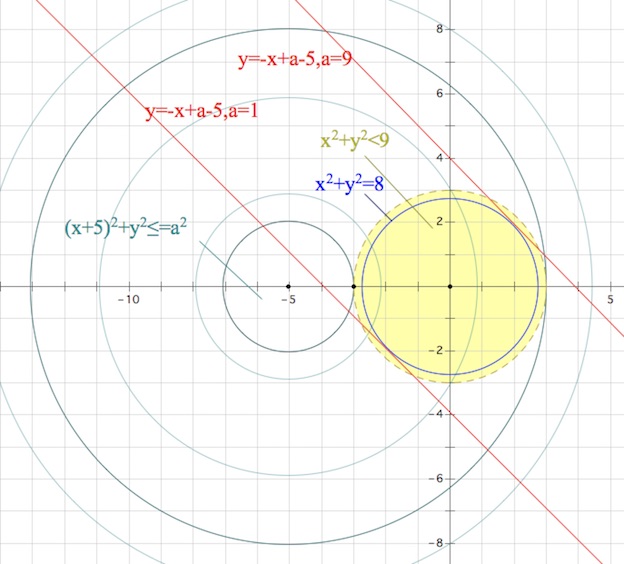
((x+5)^2+y^2-a^2)\cdot ln(9-x^2-y^2)=0,\\ ((x+5)^2+y^2-a^2)\cdot (x+y-a+5)=0;
\end{cases}$
x^2+y^2=a^2,\\xy=a^2-3a;
\end{cases}$
9y=(a-1)^2+9(x-a)^2,\\y=log_2(1+\frac{|x|}{x});&
\end{cases}$
x^2+xy-4x-2y+4=0,\\ax^2-y=4;&
\end{cases}$
x^2+y^2-2|x-y|=2,\\x^2+y^2-2a(x+y)+2a^2=2;&
\end{cases}$
Уравнения с параметром + показать
2024 1.1. (Пробник 2023) Найдите все значения а, при каждом из которых уравнение $(a+3)cos^2x+2(a^2+3a)cosx+8a^2+8a-48=0$ имеет хотя бы один корень. Ответ: {$-3$}$\cup[1,5;2,5]$ Решение 1.2. (Пробник 2023) Найдите все значения а, при каждом из которых уравнение $(a+2)cos^2x-2(a^2+2a)cosx+10a^2-5a-50 =0$ имеет хотя бы один корень. Ответ: {$-2$}$\cup[2;3]$ 2023 1.1. (ЕГЭ 2023, Досрок) Найдите все значения параметра a, при каждом из которых уравнение $\sqrt{3x-5}\cdot ln(4x^2-a^2)=\sqrt{3x-5}\cdot ln(2x+a)$ имеет ровно один корень. 1.2. (ЕГЭ 2023, Досрок) Найдите все значения параметра a, при каждом из которых уравнение $\sqrt{1-2x}\cdot ln(25x^2-a^2)=\sqrt{1-2x}\cdot ln(5x-a)$ имеет ровно один корень. Ответ: $(-\frac{5}{2};-\frac{3}{2}]\cup [\frac{1}{2};\frac{5}{2}).$ 2.1. (ЕГЭ 2023, Досрок) Найдите все значения параметра a, при каждом из которых уравнение $\sqrt{5x-3}\cdot ln(x^2-6x+10-a^2)=0$ имеет ровно один корень на отрезке $[0;3].$. Решение Ответ: $(-\frac{13}{5};-\frac{12}{5}]\cup [\frac{12}{5};\frac{13}{5}).$ 2.2. (ЕГЭ 2023, Досрок) Найдите все значения параметра a, при каждом из которых уравнение $\sqrt{7x-4}\cdot ln(x^2-8x+17-a^2)=0$ имеет ровно один корень на отрезке $[0;4].$ Ответ: $(-\frac{25}{7};-\frac{24}{7}]\cup [\frac{24}{7};\frac{25}{7}).$ 3.1. (ЕГЭ 2023, Досрок) При каких значениях параметра $a$ уравнение $\frac{|4x|-x-3-a}{x^2-x-a}=0$ имеет ровно 2 различных решения. Решение Ответ: $(-3;0)\cup(0;2)\cup(2;6)\cup(6;12)\cup(12;+\infty).$ 3.2. (ЕГЭ 2023, Досрок) При каких значениях параметра $a$ уравнение $\frac{|5x|-x-4-a}{x^2-x-a}=0$ имеет ровно 2 различных решения. Ответ: $(-4;0)\cup(0;2)\cup(2;12)\cup(12;20)\cup(20;+\infty).$ 4.1. (ЕГЭ 2023) Найдите все значения $a,$ при каждом из которых уравнение $\sqrt{x^2+6x+5}=\sqrt{a-6x}$ имеет корни (хотя бы один), из которых ровно один отрицательный. Решение Ответ: {$-31$}$\cup (-30;-6)\cup[5;+\infty).$ 4.2. (ЕГЭ 2023, резерв) Найдите все значения $a,$ при каждом из которых уравнение $\sqrt{x^2-3x+2}=\sqrt{a+3x-2}$ имеет корни (хотя бы один), из которых ровно один положительный. Ответ: {$-5$}$\cup (-4;-1)\cup[4;+\infty).$ 5.1. (ЕГЭ 2023, резерв) Найти все значения a, при каждом из которых уравнение $(2x-x^2)^2-4\sqrt{2x-x^2}=a^2-4a$ имеет хотя бы один корень. Решение Ответ: $[0;1]\cup[3;4].$ 5.2. (ЕГЭ 2023, резерв) Найти все значения a, при каждом из которых уравнение $(4x-x^2)^2-32\sqrt{4x-x^2}=a^2-14a$ имеет хотя бы один корень. Ответ: $[0;6]\cup[8;14].$ 6.1. (ЕГЭ 2023, досрок) Найдите все значения а, при каждом из которых уравнение $\sqrt{x-a}\cdot sin x=\sqrt{x-a}\cdot cos x$ имеет ровно один корень на отрезке $[0;\pi]. $ Решение Ответ: $(-\infty;0)\cup [\frac{\pi}{4};\pi].$ 6.2. (ЕГЭ 2023) Найдите все значения а, при каждом из которых уравнение $\sqrt{x+a}\cdot sin x+\sqrt{x+a}\cdot sin x=0$ имеет ровно один корень на отрезке $[-\pi;0]. $ Ответ: $(-\infty;0)\cup [\frac{\pi}{4};\pi].$ до 2023 -6. (Реальный ЕГЭ, 2021) Найдите все значения a, при каждом из которых уравнение $a|x+1|+(1-a)|x-1|+2=0$ имеет ровно два различных корня. Ответ: $(-\infty;-1)\cup (2:+\infty).$ Решение -5. (Реальный ЕГЭ, 2021) Найдите все значения $a$, при каждом из которых уравнение $|x^2-a^2|=|x+a|\sqrt{x^2-ax+4a}$ Ответ: $(-\infty;-2]\cup (0;2)\cup (2;+\infty).$ Решение -4. (Т/P, 2020) Найдите все значения параметра $a,$ при каждом из которых уравнение $(x^2-3+\sqrt{2x+a})^2=(x^2-3)^2+2x+a$ имеет единственный решение на отрезке $[0;2].$ Ответ: $[-4;-2\sqrt3]\cup (0;+\infty).$ Видеорешение -3. (Реальный ЕГЭ, 2019) При каких значениях параметра $a$ уравнение $\frac{x^2-2x+a^2-4a}{x^2-a}=0$ имеет ровно два различных решения? Ответ: $(2-\sqrt5;0)\cup (0;1)\cup (1;4)\cup (4;2+\sqrt5).$ Решение Видеорешение 1 2 New* -2. (Реальный ЕГЭ, 2019) При каких значениях параметра $a$ уравнение $\frac{|4x|-x-3-a}{x^2-x-a}=0$ имеет ровно два различных решения? Ответ:$(-3;0)\cup (0;2)\cup (2;6)\cup (6;12)\cup (12;+\infty).$ Решение -1. (Реальный ЕГЭ, 2017) Найти все значения параметра $a$, при каждом из которых уравнение $\sqrt{5x-3}\cdot ln(x^2-6x+10-a^2)=0$ имеет ровно один корень на отрезке $[0;3].$ Ответ: $(-2,6;-2,4]\cup [2,4;2,6).$ Решение 0. (резервный ЕГЭ, 2017) Найдите все значения $a$, при каждом из которых уравнение $x\sqrt{x-a}=\sqrt{4x^2-(4a+2)x+2a}$ имеет ровно один корень на отрезке $[0;1]$. Ответ: $(-\infty;0)\cup [2-\sqrt2;1].$ Решение 1. (ЕГЭ, 2016) Определите, при каких значениях параметра уравнение $\sqrt{2^x-a}+\frac{a-2}{\sqrt{2^x-a}}=1$ имеет ровно два различных решения. Ответ: $a\in (2;2,25).$ Решение 2. (ЕГЭ, 2016) Определите, при каких значениях параметра уравнение $\sqrt{15x^2+6ax+9}=x^2+ax+3$ имеет ровно три различных решения. Ответ: $[-4;-3)\cup (-3;3)\cup (3;4].$ Решение 3. (ЕГЭ, 2016) Определите, при каких значениях параметра уравнение $\frac{x-2a}{x+2}+\frac{x-1}{x-a}=1$ имеет ровно один корень. Ответ: {$\frac{-1-\sqrt{10}}{2};-2;-1;1;\frac{-1+\sqrt{10}}{2}$}.Решение 4. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых уравнение $(\frac{x-1}{x^2+1})^2-2a\cdot \frac{x-1}{x^2+1}+a^2-0,25=0$ имеет ровно три различных действительных корня. Ответ: $-0,5;-\frac{\sqrt2}{2};\frac{\sqrt2-2}{2}.$ Решение 5. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых уравнение Найдите все значения параметра $a$, при каждом из которых уравнение $log_3(ax^3+a)-2log_3\sqrt{x+1}=log_3x$ имеет хотя бы один действительный корень. Ответ: $(0;1].$ Решение 6. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых уравнение $tg(\sqrt{a^2-x^2})=0$ имеет ровно $132$ решения. Ответ: $(-66\pi;-65\pi)\cup (65\pi;66\pi).$ Решение 7. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых уравнение $|x+21|+|x+34|+|x+55|+|x+89|=ax+131$ имеет одно решение. Ответ: $(-\infty;-4]${$\frac{21}{17}$}$\cup (4;+\infty).$ Решение 8. (Т/Р Ларина) Найдите все положительные значения $a$, при каждом из которых любой корень уравнения $0,5^x-3x-\sqrt[3]x+4=a(5-log_3(1-2x))$ находится в промежутке $[-1;0].$ Ответ: $[1;2,5].$ Решение 9. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых уравнение $7^{ax^2-2x}-7^{x^2-1}=\sqrt[7]{2x-ax^2}-\sqrt[7]{1-x^2}$ имеет ровно два различных действительных корня. Ответ: $(-\infty;1)\cup (1;2).$ Решение 10. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых уравнение $x^2-acos\frac{\pi x}{2}+a^2-6=0$ имеет ровно один корень. Ответ: $3.$ Решение 11. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых уравнение $|x^2-2x-3|-ax=2(3a+2)$ имеет ровно три корня. Ответ: $-\frac{4}{9};0.$ Решение 12. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых уравнение $\frac{a^3-(x+2)a^2+xa+x^2}{a+x}=0$ имеет ровно один корень. Ответ: $1;3.$ Решение 13. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых уравнение $2|2|x|-a^2|=x-a$ имеет ровно три корня. Ответ: $-2;-0,5.$ Решение 14. (Т/Р Ларина) Найти все значения параметра $a$, при каждом из которых уравнение $a|x-1|=x+2$ имеет ровно один корень. Укажите этот корень для каждого такого значения $a.$ Ответ: $a\in (-1;1]$: $x=\frac{a-2}{a+1}.$ Решение 15. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых корни уравнения $x^4+(a-5)x^2+(a+2)^2=0$ являются четырьмя последовательными членами арифметической прогрессии. Ответ: $-5;-\frac{5}{13}.$ Решение 16. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых уравнение $4^{a^2}\cdot log_2(|x^2-6x+8|+2)+2^{3a-|x^2-6x+8|}\cdot log_2(\frac{1}{2+3a-2a^2})=0$ имеет ровно два различных действительных корня. Ответ: $(\frac{1}{2};1)\cup ${$0;1,5$}. Решение 17. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых уравнение $a^x+1-a^2=log_a\frac{1}{x}$ имеет решение, причем любой его корень находится в промежутке $[1; 2]$. Ответ: $[\frac{1}{2};1)\cup [\frac{1+\sqrt5}{2};+\infty).$ Решение 18. (Т/Р Ларина) Найти все значения параметра $a$, при которых больший корень уравнения $x^2+\frac{x+4}{\sqrt3}sin2a-16=0$ на $\sqrt{\frac{2}{3}}$ больше, чем квадрат разности корней уравнения $x^2-xsina+\frac{cos^2a}{4}-1=0.$ Ответ: $-\frac{5\pi}{24}+\pi n,$ $\frac{\pi}{24}+\pi n$, $n\in Z.$ Решение 19. (Т/Р Ларина) При каких значениях параметра $a$ уравнение имеет ровно одно решение? $(x-3)(x+1)+3(x-3)\sqrt{\frac{x+1}{x-3}}=(a-1)(a+2).$ Ответ:$-0,5.$ Решение 20. (Диагностич., 2013) Найдите все значения параметра $a$, при каждом из которых уравнение $|x-a^2+a+2|+|x-a^2+3a-1|=2a-3$ имеет корни, но ни один из них не принадлежит интервалу $(4;19).$ Ответ: $[4;7].$ Решение 21. (Т/Р Ларина) Найдите все значения параметра а, при которых уравнение $x-2=\sqrt{-2(a+2)x+2}$ имеет единственное решение. Ответ: $(-\infty;-1,5].$ Решение 22. (Диагностич., 2014) Найдите все значения а, при каждом из которых уравнение $x^2-|x-a+6|=|x+a-6|-(a-6)^2$ имеет единственный корень. Ответ: $1;5.$ Решение 23. (ЕГЭ, 2013) Найти все значения $a$, при каждом из которых уравнение $ax+\sqrt{-5-6x-x^2}=5a+2$ имеет единственное решение. Ответ: $[-1;-\frac{1}{3})\cup${0}. Решение 24. (Досрочн. ЕГЭ, 2013) Найдите все значения $a$, для каждого из которых уравнение $\log_{1-x}(a-x+2)=2$ имеет хотя бы один корень, принадлежащий промежутку $[-1;1).$ Ответ: $(-1; 2)\cup(2; 3]$. Решение 25. (Досрочн. ЕГЭ, 2013) Найдите все значения параметра а, при которых уравнение $a|x-4| = \frac{5}{x+1}$ на промежутке $[0; +\infty)$ имеет ровно три корня. Ответ: $\frac{2}{9},\;(\frac{2}{5}; + \infty)$. Решение 26. (Т/Р Ларина) Найдите все значния параметра $a$, при каждом из которых уравнение $\frac{2a^2-(x+3)a-x^2+3x}{x^2-9}=0$ имеет ровно один корень. Ответ: {$-3;0;1$}. Решение 27. (Т/Р Ларина) Найдите все значния параметра $a$, при каждом из которых уравнение $2\cdot (|x-2|+|x|)^2-3(a-2)\cdot (|2-x|+|x|)+a^2-3a=0$ имеет не менее трех различных корней. Ответ: {$4$}$\cup [5;6)\cup (6;+\infty).$ Решение 28. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых уравнение $2cos2x+2asinx+a-1=0$ имеет наибольшее количество решений на отрезке $[-\pi;\frac{17\pi}{6}]$. Чему равно это количество? Ответ: $(-3;-2)\cup (-2;-1]\cup [0;1);$ $8$ корней. Решение 29. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых уравнение $x^4-x^2+\frac{|ax|}{3\sqrt3}+a^3-a^2-2a=0$ имеет ровно три корня. Для каждого такого $a$ укажите корни. Ответ: три корня при $a=0$ или $a=2;$ $a=0$: $0$; $\pm 1$; $a=2$: $0$; $\pm \frac{1}{\sqrt3}$. Решение 30. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых уравнение $ax^2+x+a-1=0$ имеет два различных корня $x_1,x_2,$ удовлетворяющих неравенству $|\frac{1}{x_1}-\frac{1}{x_2}|>1$. Ответ: $(0;1)\cup(1;\frac{6}{5}).$ Решение 31. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых уравнение $log_2^2|4-x^2|-2a\cdot log_2|x^2-4|+a+6=0$ имеет ровно четыре различных корня. Ответ: {$-2$}$\cup (3;\frac{10}{3}).$ Решение 32. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых уравнение $4sin^2x-4asinx+a^3-a^2=0$ имеет ровно один корень на промежутке $[-\frac{\pi}{2};2\pi].$ Ответ: $\pm 2.$ Решение 33. (Т/Р Ларина) При каких положительных значениях параметра $a$ уравнение $||2x|-4|=|x^2-a|$ имеет ровно $4$ решения? Ответ: {$3$}$\cup (4;+\infty).$ Решение 34. (Т/Р, 2017) Найдите все значения параметра $a$, при каждом из которых уравнение $\sqrt{x^4-16x^2+64a^2}=x^2+4x-8a$ имеет ровно три решения. Ответ: $(-\infty;-2)\cup (-2;0).$ Решение 35. (Т/Р Ларина) Найдите все значния параметра $a$, при каждом из которых уравнение $lg(x^2(x-2a)+x(2+a)+1-a^2)=lg(x^2-a^2x+2x-a^2+1)$ имеет ровно два различных действительных корня. Ответ: $(-\infty;-2)\cup (-1;\frac{1-\sqrt5}{2}]\cup${0}$\cup[1;\frac{1+\sqrt5}{2})$. Решение 36. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых уравнение $log^2_x(2ax+1-a^2)-2log_x(2ax+1-a^2)=0$ имеет более двух корней. Ответ: {$0$}$\cup (1;2)\cup (2;+\infty).$ Решение 37. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых уравнение $\sqrt{4x-x^2}\cdot log_2(x^2-2ax+a^2)=0$ имеет ровно три различных корня. Ответ: $(-1;0)\cup (0;1]\cup [3;4)\cup (4;5).$ Решение 38. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых уравнение $|x-2|+|x|-ax=2(a-1)$ имеет ровно один корень. Ответ: $(-\infty;-2)\cup ${$1$}$\cup [2;+\infty).$ Решение 39. (Т/Р Ларина) Найти все $a$, при каждом из которых уравнение $x-2=\frac{(a+1)(a-5)}{x+4}$ имеет ровно один корень на промежутке $(-\infty;0)$. Ответ: $(-\infty;-1)\cup (-1;1]\cup ${$2$}$\cup [3;5)\cup (5;+\infty).$ Решение 40. (Т/Р Ларина) Найти все значения $a$, при каждом из которых уравнение $\sqrt{a-(a+1)(2x+4)=x+1$ имеет ровно один корень. Ответ: $(-\infty;-2)\cup\left \{ \frac{-1-\sqrt5}{2} \right \}.$ Решение 41. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых уравнение $lg(1-x)+lg(a^2-x^2)=lg(x-a)^2$ имеет ровно одно решение. Ответ: $(-\infty;0)\cup(0;1]\cup \left \{ 2 \right \}.$ Решение 42. (Т/Р 281 Ларина) При каких значениях параметра $a$ уравнение $6\cdot (\frac{x}{x^2+1})^2-\frac{(6a+1)x}{x^2+1}-12a^2+8a-1=0$ имеет ровно $4$ корня? Ответ: $(0;\frac{1}{6})\cup(\frac{1}{6};\frac{5}{18})\cup (\frac{5}{18};\frac{5}{12}).$ Решение 43. (Т/Р 283 Ларина) Найдите все значения параметра $a,$ при каждом из которых уравнение $log_{3x-4}(a+9x+5)=-1$ имеет единственный корень на промежутке $(\frac{4}{3};2].$ Ответ: $[-22,5;-19)\cup (-19;+\infty).$ Решение
Решение Ответ: $(-\frac{10}{3};\frac{7}{3}]\cup [\frac{10}{3};+\infty).$
имеет ровно два различных корня.
Неравенства с параметром + показать
1.1. (ЕГЭ 2023, Досрок) Найдите все значения a, при каждом из которых множество решений неравенства $\large\frac{5-a-(a^2-2a+1)sinx}{cos^2x+a^2+2}<1$ содержит отрезок $[0;\frac{2\pi}{3}].$ Решение Ответ: $(-\infty;-2)\cup (\frac{1+\sqrt{17}}{4};+\infty).$ $\large\frac{9a-(a^2-a+3)sinx+1}{2cos^2x+a^2+3}<1$ содержит отрезок $[0;\frac{2\pi}{3}].$ Ответ: $(-\infty;\frac{4}{3})\cup (3;+\infty).$ 1. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых множество решений неравенства $|x-a|+|x+3a|\geq x^2+a^2$ содержит ровно четыре целых значения $x$. Ответ: $(-2;0)\cup (0;2)$. Решение 2. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых неравенство $log_{2}^3x-3\log^2_2x<(134+a)log_2x$ выполняется для любых $x\in [2;4\sqrt2].$ Ответ: $(-135,25;+\infty).$ Решение 3. (Т/Р Ларина) Для каждого значения $a$ решите неравенство $ax^2-(2a+1)x+2>0$. Ответ: $a\in (-\infty;0):$ $x\in (\frac{1}{a};2);$ $a=0: (-\infty;2);$ $a\in (0;\frac{1}{2}]:$ $x\in (-\infty;2)\cup (\frac{1}{a};+\infty);$ $a\in (\frac{1}{2};+\infty):$ $x\in (-\infty;\frac{1}{a})\cup (2;+\infty).$ 4. (Т/Р Ларина) Найдите все значения параметра $a$, при каждом из которых неравенство $x^2+2|x-a|-4x\leq -a$ имеет единственное целочисленное решение. Для найденных значений $a$ выпишите это решение. Ответ: $a\in [-1;0)$: $1$; $a\in (\frac{5}{3};\frac{8}{3}]$: $2$; $a=3$: $3.$ Решение 5. (Т/Р Ларина) При каких $a$ для всех $x\in [2;\frac{5}{2}]$ выполняется неравенство $log_{|x-a|}(x^2+ax)\leq 2$ ? Ответ: ($-2;0]\cup(1,5;2$)$\cup$($2,5;3)\cup[7,5;+\infty$). Решение 6. (Т/Р Ларина) Найти все значения действительного параметра $a$, для которых неравенство $4^x-a\cdot 2^x-a+3\leq 0$ имеет хотя бы одно решение. Ответ: [$2;+\infty$). Решение 7. (МГУ, 2013) Найдите минимальное значение разности [latexpage] $x-4a$ при условии $x^2+4a^2\leq 4.$ Ответ: $-2\sqrt5.$ Решение 8. (Т/Р Ларина) Определите, при каких значениях параметра $a$ пересечение множеств $(x-a+1)^2+(y-2a-3)^2\leq 80$, $(x-2a+3)^2+(y-4a+1)^2\leq 20a^2$ представляет собой круг. Ответ: $(-\infty;-6]\cup[-\frac{2}{3};0)\cup (0;+\infty).$ Решение 9. (Т/Р Ларина) При каждом значении параметра $a$ решить неравенство $\frac{log_2(4x-3)-2log_2x}{|x-2|-a}\geq 0$. Ответ: $a\in (-\infty;0)$: $x\in [1;3];$ $a\in [0;1)$: $x\in [1;2-a)\cup (a+2;3];$ $a=1$: решений нет; $a\in (1;\frac{5}{4})$: $x\in (2-a;1]\cup [3;a+2);$ $a\in [\frac{5}{4};+\infty)$: $x\in (\frac{3}{4};1]\cup [3;a+2).$ Решение 10. (Т/Р Ларина) При каких значениях параметра $a$ для всякого $x$ из $[0;7]$ верно неравенство $||x+2a|-3a|+||3x-a|+4a|\leq 7x+24.$ Ответ: $[-3;4].$ Решение 11. (Т/Р Ларина) При каких значениях параметра $a$ среди решений неравенства $log_2(x-100)-log_{\frac{1}{2}}\frac{|x-101|}{105-x}+log_2\frac{|x-103|(105-x)}{x-100}>a.$ содержится единственное целое число? Ответ:$[0;log_23).$ Решение
3.1. (ЕГЭ 2023, Досрок) Найдите все значения a, при каждом из которых множество решений неравенства
Функции с параметром + показать
1. (Т/Р Ларина) Для каждого $a$ определите наибольшее значение функции $f(x)=x^3-3ax^2$ на отрезке $[-2; 2]$. Ответ:$a\in (-\infty;\frac{2}{3})$: $8-12a;$ $a\in [\frac{2}{3};+\infty)$: $0.$ Решение 2. (Т/Р Ларина) График функции $f(x)=x^3+ax^2+bx+c,c<0$, пересекает ось ординат в точке $A$ и имеет ровно две общие точки $M$ и $N$ с осью абсцисс. Прямая, касающаяся этого графика в точке $M$, проходит через точку $A$. Найдите $a,b$ и $c$, если площадь треугольника $AMN$ равна $1$. Ответ: $a=-4,$ $b=5,$ $c=-2.$ Решение 3. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых наибольшее значение функции $f(x)=133ax-|x^2-10x+24|$ больше $-2.$ Ответ: $(-\infty;-\frac{10+2\sqrt2}{2})\cup(-\frac{1}{266};+\infty).$ Решение 4. (Т/Р Ларина) Парабола $p_2$ симметрична параболе $p_1$, заданной уравнением $y=ax^2 (a>0)$, относительно точки $T(b;ab^2), b>0.$ Некоторая прямая пересекает каждую параболу ровно в одной точке: $p_1$ – в точке $A_1,$ $p_2$ – в точке $A_2$ так, что угол $A_1A_2T$ прямой. Касательная к параболе $p_1$, проведенная в точке $T$, пересекает прямую $A_1A_2$ в точке $K$. Найдите отношение, в котором точка $K$ делит отрезок $A_1A_2.$ Ответ: $1:1$. Решение 5. (Т/Р Ларина) Найдите все $a$, при каждом из которых функция $f(x)=x^3-3ax^2+3a^2x-3|x|+3$ имеет ровно два экстремума на промежутке (‐2;3). Ответ: $(-1;2).$ Решение 6. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых для любого $x$ из промежутка $[3;9)$ значение выражения $log^2_3x-6$ не равно значению выражения $(a-4)log_3x.$ Ответ: $(-\infty;-1)\cup [3;+\infty).$ Решение 7. (Т/Р Ларина) Найдите все значения $a$, при каждом из которых функция $f(x)=||x|-2|-ax+8a$ принимает значение, равное 2, в двух различных точках. Ответ: $(-1;0)\cup(\frac{1}{5};\frac{1}{3}).$ Решение 8. (ДЕМО, 2014) Найдите все значения а, при каждом из которых наименьшее значение функции $f(x)=2ax+|x^2-8x+7|$ больше 1. Ответ:$(\frac{1}{2};5)$ Решение 9. (Т/Р Ларина) Уравнение $2x^3+ax^2+bx+c=0$ с целыми коэффициентами имеет три различных корня. Оказалось, что первый корень является синусом, второй – косинусом, а третий – тангенсом одного и того же угла. Найдите все такие уравнения. Ответ: $2x^3+2x^2-x-1=0.$ Решение 10. (Т/Р Ларина) Для каждого значения параметра $a$ найдите точку максимума функции $f(x)=x^3(3x-8a)+6(a^2-1)x^2.$ Ответ: $a\in (-\infty;-1):$ $a+1;$ $a=-1:$ нет; $a\in (-1;1):$ $0;$ $a=1:$ нет; $a\in (1;+\infty):$ $a-1$.