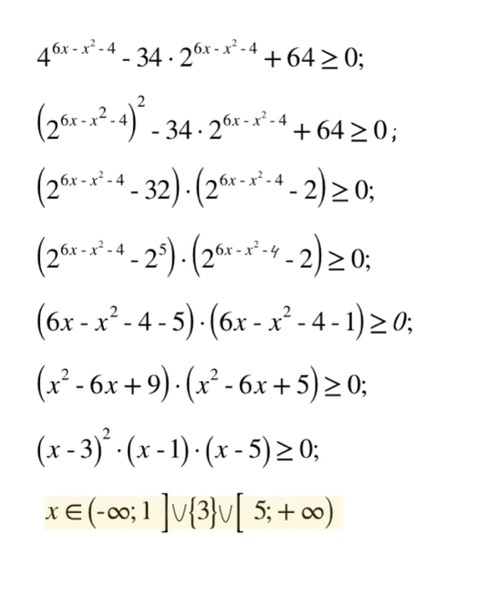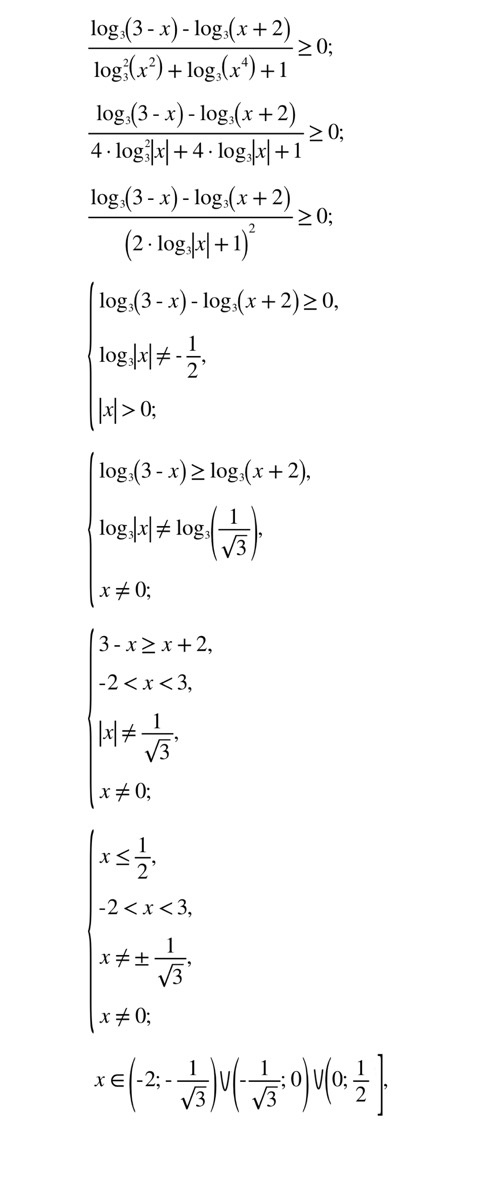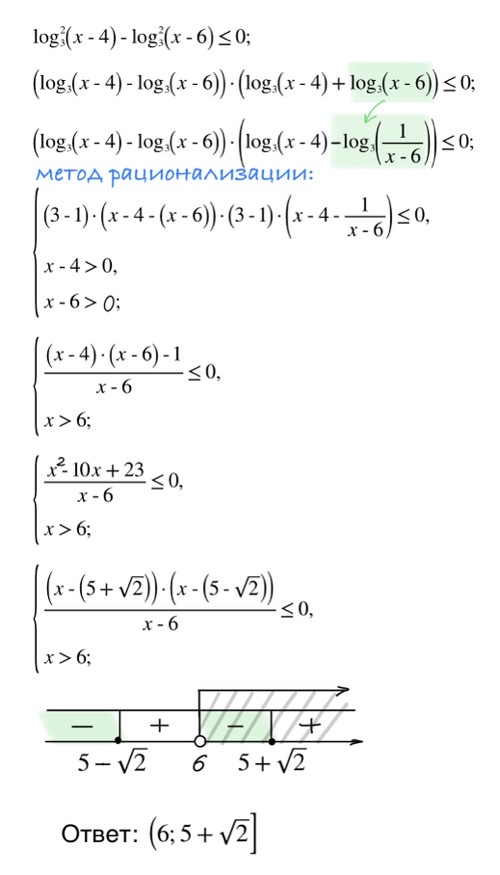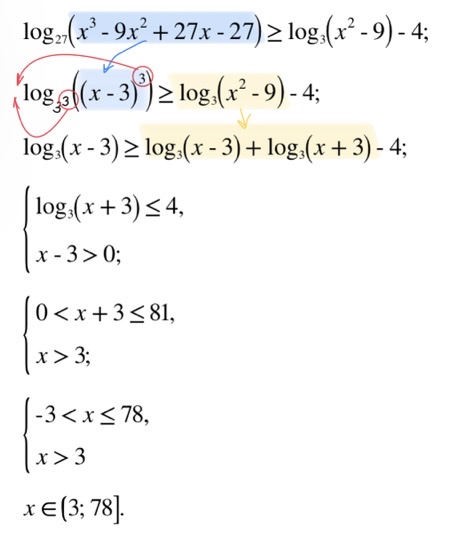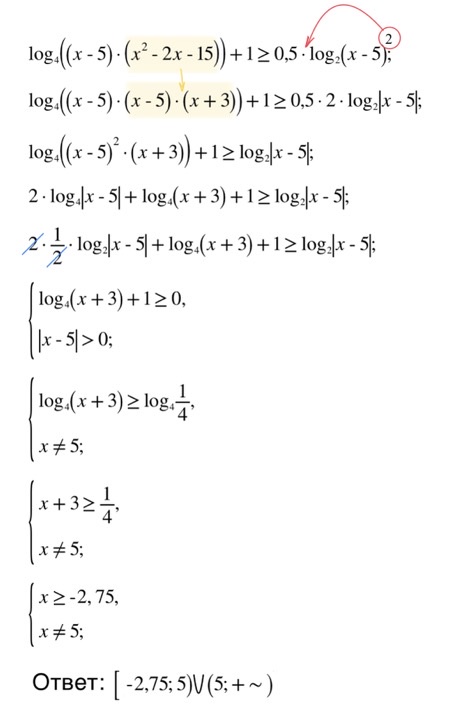См. также подборку реальных неравенств ЕГЭ для подготовки
2024
1.1. (Пробник 2023) Решите неравенство: $\frac{6}{|x-2|}-\frac{2}{|x+6|}\geq 1.$
Решение Ответ: $[-2;2)\cup (2; 2\sqrt{13}].$
1.2. (Пробник 2023) Решите неравенство: $\frac{5}{|x-2|}-\frac{3}{|x+6|}\geq 1.$
Ответ: $[-6+2\sqrt6;2)\cup (2; 6].$
2023
1.1. (Пробный ЕГЭ-23) Решите неравенство:
$\log_{4}( x-3) ( 10+3x-x^{2})) +\log_{4}\dfrac{7-x}{10+3x-x^ {2}}\leq -1+\log _{4}( 2x+4).$
Ответ: $ ( 3; 4].$ Решение
1.2. (Пробный ЕГЭ-23) Решите неравенство:
$\log_{5}( x-2)( 24+2x-x^{2}) ) +\log_{5}\dfrac{9-x}{24+2x-x^{2}}\leq -1+\log _{5}(12x).$
Ответ: $(2;3,6]\cup[5;6).$
2.1. (Досрок, 2023) Решите неравенство:
$\large\frac{9^x-3^{x+1}-19}{3^x-6}+\frac{9^{x+1}-3^{x+4}+2}{3^x-9}\leq 10\cdot 3^x+3.$
Ответ: $(-\infty;1]\cup(log_36;2).$ Решение
2.2. (Досрок, 2023) Решите неравенство:
$\large\frac{4^x+2^{x+1}-36}{2^x-5}+\frac{4^{x+1}-2^{x+5}+4}{2^x-8}\leq 5\cdot 2^x+7.$
Ответ: $(-\infty;2]\cup(log_25;3).$
3.1. (Досрок 2023) Решите неравенство:
$\large\frac{8^{x+\frac{2}{3}}-9\cdot 4^{x+\frac{1}{2}}+13\cdot2^x-13}{4^{x+\frac{1}{2}}-9\cdot 2^{x}+4}\leq 2^{x+1}-\frac{1}{2^x-2}+\frac{3}{2^{x+1}-1}.$
Ответ: $(-\infty;-1)\cup(-1;1)\cup [log_23;2).$ Решение
3.2. (Досрок 2023) Решите неравенство:
$\large\frac{27^{x+\frac{1}{3}}-10\cdot 9^x+10\cdot 3^x-5}{9^{x+\frac{1}{2}}-10\cdot 3^{x}+3}\leq 3^{x}+\frac{1}{3^x-2}+\frac{1}{3^{x+1}-1}.$
Ответ: $(-\infty;-1)\cup(-1;0]\cup (log_32;1).$
4.1. (Досрок 2023) Решите неравенство:
$\large\frac{4^x-2^{x-3}+7}{4^x-5\cdot 2^x+4}\leq \frac{2^x-9}{2^x-4}+\frac{1}{2^{x}-6}.$
Ответ: $(-\infty;0)\cup(0;2)\cup (log_26;3].$ Решение
4.2. (Досрок 2023) Решите неравенство: $\large 2^x+\frac{2^{x+2}}{2^x-4}+\frac{4^x+7\cdot 2^x+20}{4^x-3\cdot 2^{x+2}+32}\leq 1.$
Ответ: $(-\infty;0]\cup[log_23;2)\cup (2;3).$
5.1. (ЕГЭ 2023) Решите неравенство:
$(log^2_{0,2} (x-5)-log_5(x^2-10x+25)+1)\cdot log_5(x-7)\leq 0$
Решение Ответ: $(7;8]\cup${$10$}
5.2. (ЕГЭ 2023) Решите неравенство:
$(log^2_{0,25} (x+3)-log_4(x^2+6x+9)+1)\cdot log_4(x+2)\leq 0$
Ответ: $(-2;-1]\cup${$1$}
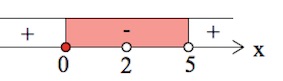
6.1. (ЕГЭ 2023) Решите неравенство:
$log_{4} ((x-5)(x^2-2x-15))+1\geq 0,5log_2(x-5)^2$
Решение Ответ: $[-2\frac{3}{4}; 5)\cup (5;+\infty)$
6.2. (ЕГЭ 2023) Решите неравенство:
$log_{25} ((x-4)(x^2-2x-8))\geq 0,5log_5(x-4)^2+1$
Ответ: $[23;+\infty )$
7.1. (ЕГЭ 2023) Решите неравенство:
$log_{27} (x^3-9x^2+27x-27)\geq log_3(x^2-9)-4$
Решение Ответ: $( 3;78]$
7.2. (ЕГЭ 2023) Решите неравенство:
$log_{8} (x^3-3x^2+3x-1)\geq log_2(x^2-1)-5$
Ответ: $( 1;31]$
8.1. (ЕГЭ 2023) Решите неравенство:
$log^2_3(x-4)-log^2_3(x-6)\leq 0$
Решение Ответ: $(6;5+\sqrt{2}]$
8.2. (ЕГЭ 2023) Решите неравенство:
$log^2_5(x-4)-log^2_5(x-6)\leq 0$
Ответ: $(6;5+\sqrt{2}]$
9.1. (ЕГЭ 2023) Решите неравенство:
$\frac{log_3(3-x)-log_3(x+2)}{log_3^2(x^2)+log_3(x^4)+1}\geq 0$
Решение Ответ: $(-2;-\frac{\sqrt{3}}{3})\cup(-\frac{\sqrt{3}}{3};0)\cup(0;\frac{1}{2}]$
9.2. (ЕГЭ 2023) Решите неравенство:
$\frac{log_5(4-x)-log_5(x+5)}{log_3^2(x^2)-log_3(x^4)+1}\geq 0$
Ответ: $(-5;-\sqrt{3})\cup(-\sqrt{3};-0,5]$
10.1. (ЕГЭ 2023, резерв) Решите неравенство:
$\large 4^{6x-x^2-4}-34\cdot3^{6x-x^2-3}+64\geq 0$
Решение Ответ: $(-\infty;1]\cup${$3$}$\cup (5;+\infty).$
10.2. (ЕГЭ 2023, резерв) Решите неравенство:
$\large 9^{4x-x^2-1}-36\cdot3^{4x-x^2-1}+243\geq 0$
Ответ: $(-\infty;1]\cup${$2$}$\cup (3;+\infty).$
до 2023
-11. (Реальный ЕГЭ, 2021) Решите неравенство:
$(9^x-3^{x+1})^2+8\cdot 3^{x+1}<8\cdot 9^x+20.$
Ответ: $(-\infty;0)\cup (log_32;log_35).$ Решение
-10. (Реальный ЕГЭ, 2021) Решите неравенство: $\large 16^{\frac{1}{x}-1}-4^{\frac{1}{x}-1}-2\geq 0.$
Ответ: $(0;\frac{2}{3}].$ Решение
-9. (Демо ЕГЭ, 2020) Решите неравенство
$log_{11}(8x^2+7)-log_{11}(x^2+x+1)\geq log_{11}(\frac{x}{x+5}+7).$
Ответ: $(-\infty;-12]\cup (-\frac{35}{8};0].$ Видеорешение
-8. (Реальный ЕГЭ, 2019) Решите неравенство
$log_{\frac{1}{3}}(18-9x)<log_{\frac{1}{3}}(x^2-6x+5)+ log_{\frac{1}{3}}(x+2).$
Ответ: $(-2;1).$ Решение Видеорешение
-7. (Реальный ЕГЭ, 2019) Решите неравенство $log_4(6-6x)<log_4(x^2-5x+4)+ log_4(x+3).$
Ответ: $(-2;1).$ Решение
-6. (Реальный ЕГЭ, 2018) Решите неравенство
$log_7(2x^2+12)-log_7(x^2-x+12)\geq log_7(2-\frac{1}{x}).$
Ответ: $(\frac{1}{2};\frac{4}{3}]\cup [3;+\infty).$ Решение Видеорешение
-5. (Досрочный резервный ЕГЭ, 2018) Решите неравенство $\large \frac{6^x-4\cdot 3^x}{x\cdot 2^x-5\cdot 2^x-4x+20}\leq \frac{1}{x-5}.$
Ответ: $[0;2)\cup (2;5).$ Решение Видеорешение
-4. (Досрочный ЕГЭ, 2018) Решите неравенство $3^{x^2}\cdot 5^{x-1}\geq 3.$
Ответ: $(-\infty;-1-log_35]\cup [1;+\infty).$ Решение Видеорешение
-3. (Резервный ЕГЭ, 2017) Решите неравенство $\large\frac{1}{3^x-1}+\frac{9^{x+\frac{1}{2}}-3^{x+3}+3}{3^x-9}\geq 3^{x+1}.$
Ответ: $(0;1]\cup (2;+\infty).$ Решение
-2. (Резервный ЕГЭ, 2017) Решить неравенство $9^{4x-x^2-1}-36\cdot 3^{4x-x^2-1}+243\geq 0.$
Ответ: $(-\infty;1]\cup$ {$2$}$\cup[3;+\infty).$ Решение Видеорешение
-1. (Реальный ЕГЭ, 2017) Решить неравенство $\frac{log_2(4x^2)+35}{log_2^2x-36}\geq -1.$
Ответ: $(0;\frac{1}{64})\cup${$\frac{1}{2}$}$\cup (64;+\infty).$ Решение
0. (Реальный ЕГЭ, 2017) Решить неравенство $\frac{log_4(64x)}{log_4x-3}+\frac{log_4x-3}{log_4(64x)}\geq \frac{log_4x^4+16}{log_4^2x-9}.$
Ответ: $(0;\frac{1}{64})\cup${$4$}$\cup (64;+\infty).$ Решение
1. (Досрочн. ЕГЭ, 2017) Решите неравенство $log_2^2(25-x^2)-7log_2(25-x^2)+12\geq 0.$
Ответ: $(-5;-\sqrt{17}]\cup [-3;3]\cup [\sqrt{17};5).$ Решение Видеорешение
2. (Резервн. ЕГЭ, 2016) Решите неравенство
$\frac{9^x-3^{x+1}-19}{3^x-6}+\frac{9^{x+1}-3^{x+4}+2}{3^x-9}\leq 10\cdot 3^x+3.$
Ответ: $(-\infty;1]\cup (log_36;2).$ Решение Видеорешение
3. (ЕГЭ, 2016) Решите неравенство
$\frac{25^x-5^{x+2}+26}{5^x-1}+\frac{25^x-7\cdot 5^{x}+1}{5^x-7}\leq 2\cdot 5^x-24.$
Ответ: $(-\infty;0)\cup [1;log_57).$ Решение
4. (Т/Р, 2016) Решите неравенство
$\large 2^{\frac{x}{x+1}}-2^{\frac{5x+3}{x+1}}+8\leq 2^{\frac{2x}{x+1}}.$
Ответ: $(-\infty;-1)\cup [0;+\infty).$ Решение
5. (Досрочн. ЕГЭ, 2016) Решите неравенство
$(5x-13)log_{2x-5}(x^2-6x+10)\geq 0.$
Ответ: $(2,5;2,6]\cup (3;+\infty)$. Решение Видеорешение
6. (ЕГЭ, 2015) Решите неравенство
$\frac{3}{(2^{2-x^2}-1)^2}-\frac{4}{2^{2-x^2}-1}+1\geq 0.$
Ответ: $(-\infty;-\sqrt2)\cup (-\sqrt2;-1]\cup${$0$}$\cup [1;\sqrt2)\cup(\sqrt2;+\infty).$ Решение
7. (Т/Р 2013) Решите систему неравенств
$\begin{cases}
9^x-5\cdot 3^x+4\geq 0,\;(1)&
\\log_{\frac{3x^2+4x+1}{4x+1}}|\frac{x}{2}|\leq 0;\;(2)
\end{cases}$
Ответ: $(-\frac{1}{3};0)\cup[log_53;1].$ Решение
8. (Т/Р 2013) Решите систему неравенств
$\begin{cases}
1-\frac{2}{|x|}\leq \frac{23}{x^2},\;(1)&
\\ \frac{2-(x-5)^{-1}}{2(x-5)^{-1}-1}\leq -0,5;\;(2)
\end{cases}$
Ответ: $[2-2\sqrt6;0 )\cup (0;6).$ Решение
9. (Т/Р 2013) Решите систему неравенств
$\begin{cases}log_{6x^2-x-1}(2x^2-5x+3)\geq 0,\\\frac{12x^2-31x+14}{4x^2+3x-1}\leq 0;&\end{cases}$
Ответ: $(-2;-1)\cup [\frac{1}{10};\frac{1}{6})\cup ${$\frac{3}{2}$}. Решение
10. (ДЕМО 2014) Решите систему неравенств
$\begin{cases}
4^x≤9\cdot 2^x+22,&
\\ log_3(x^2-x-2)≤1+log_3\frac{x+1}{x-2};
\end{cases}$
Ответ: $(2;log_211].$ Решение
11. (ЕГЭ 2013) Решите систему неравенств
$\begin{cases}
log_{6-x}\frac{x+5}{(x-6)^{12}}≥ – 12,&
\\ x^3+7x^2+\frac{30x^2+7x-42}{x-4}≤ 7;&
\end{cases}$
Ответ: {$-4;0$}$\cup [3;5).$ Решение
12. (Т/Р А. Ларина) Решите неравенство
$log_4(x^2-4)^2+log_2(\frac{x-1}{x^2-4})>0.$
Ответ: $(-2;0)\cup (2;+\infty).$ Решение
13. (Т/Р А. Ларина) Решите неравенство
$log_5(2+x)(x-5)>log_{25}(x-5)^2.$
Ответ: $(-\infty;-3)\cup (5;+\infty).$ Решение
14. (Т/Р А. Ларина) Решите неравенство
$\sqrt{7-log_2x^2}+log_2x^4>4.$
Ответ: $[-8\sqrt2;-\sqrt[8]{8})\cup (\sqrt[8]{8};8\sqrt2].$ Решение
15. (Т/Р А. Ларина) Решите неравенство
$\frac{1}{2}log_{x-1}(x^2-8x+16)+log_{4-x}(-x^2+5x-4)>3.$
Ответ: $(2;2,5)\cup (2,5;3).$ Решение Видеорешение
16. (Т/Р А. Ларина) Решите неравенство
$log_2(5-x)log_2(x+1)\leq log_2\frac{(x^2-4x-5)^2}{16}.$
Ответ: $(-1;1]\cup [3;5).$ Решение
17. (Т/Р А. Ларина) Решите неравенство
$\large\frac{x^4-2x^2+1}{2x^2-x-6}\geq \frac{1-2x^2+x^4}{2x^2-7x+6}.$
Ответ: $(-\infty;-1,5)\cup${$-1;1$}$\cup(1,5;2).$ Решение
18. (Т/Р А. Ларина) Решите неравенство
$\large\frac{(3^x-3)^3}{2\cdot 3^x-4}\leq \frac{27^x-2\cdot 3^{2x+1}+3^{x+2}}{3^x-9^x+2}.$
Ответ: $[\frac{1}{2};log_32)\cup${$1$}. Решение
19. (Т/Р А. Ларина) Решите неравенство
$log_x(log_2(4^x-6))\leq 1.$
Ответ: $(log_47;log_23].$ Решение
20. (Т/Р А. Ларина) Решите неравенство
$\large\frac{4^{x^2-2x}-16\cdot 2^{(x-1)^2}+35}{1-2^{(x-1)^2}}\leq 4^x\cdot 2^{(x-2)^2}.$
Ответ: $(-\infty;1)\cup (1;+\infty).$ Решение
21. (Т/Р А. Ларина) Решите неравенство
$\large\frac{log_{x+0,5}(4^x-3\cdot 2^{x+1}+8)}{log_{\sqrt{x+0,5}}2}\leq x.$
Ответ: $[2-log_23;0,5)\cup (0,5;1)\cup (2;+\infty).$ Решение
22. (Т/Р А. Ларина) Решите неравенство
$\sqrt{1+x^2}-x\leq \frac{5}{2\sqrt{1+x^2}}.$
Ответ: $[-\frac{3}{4};+\infty).$ Решение
23. (Т/Р А. Ларина) Решите неравенство
$\frac{1}{2}log_{134+tg^2(\frac{x}{2})}(21x+16)<log_{134+tg^2(\frac{x}{2})}(20+\sqrt{x-4}).$
Ответ: $[4;3\pi)\cup (3\pi;5\pi)\cup (5\pi;7\pi)\cup (7\pi;9\pi)\cup (9\pi;29).$ Решение
24. (Т/Р А. Ларина) Решите неравенство
$log_2(log_3(log_4(log_5^2(133-2x)+7)+25)-1)\leq 1.$
Ответ: $[4;66,496].$ Решение
25. (Т/Р А. Ларина) Решите неравенство
$\large\frac{x^3-18x^2+89x-132}{(\sqrt x-2)(5^x-25)(|x|-1)}\leq 0.$
Ответ: $(1;2)\cup [3;4)\cup(4;11].$ Решение
26. (Т/Р А. Ларина) Решите неравенство
$2\sqrt{x+131}-\frac{5}{\sqrt{x+131}-3}\leq 15.$
Ответ: $[-131;-124,75]\cup (-122;-67].$ Решение
27. (Т/Р А. Ларина) Решите неравенство
$x^2+x\sqrt{3-3x^2}\geq 0,5+x.$
Ответ: $[-1;-sin\frac{5\pi}{18}]\cup [\frac{1}{2};sin\frac{7\pi}{18}].$ Решение
28. (Т/Р А. Ларина) Решите неравенство
$log_{x+1}2\leq log_{3-x}2.$
Ответ: $(-1;0)\cup [1;2).$ Решение
29. (Т/Р А. Ларина) Решите неравенство
$\frac{2x^2}{x+3}+\frac{x+3}{x^2}\leq 3.$
Ответ: $(-\infty;-3)\cup [\frac{1-\sqrt{13}}{2};-1]\cup [\frac{3}{2};\frac{1+\sqrt{13}}{2}].$ Решение
30. (Т/Р А. Ларина) Решите неравенство
$log_{2x}(x+4)\cdot log_x(2-x)\leq 0.$
Ответ: $(0,5;1)\cup (1;2).$ Решение
31. (Т/Р А. Ларина) Решите неравенство
$log_{(x-2)^2}\frac{5-x}{4-x}\leq 1+log_{(2-x)^2}\frac{1}{x^2-9x+20}.$
Ответ: $(1;2)\cup (2;3)\cup [3,5;4)\cup (5;+\infty).$ Решение
33. (Т/Р А. Ларина) Решите неравенство
$\large\frac{2\sqrt{x+3}}{x+1}\leq \frac{3\sqrt{x+3}}{x+2}$.
Ответ: {$-3$}$\cup (-2;-1)\cup [1;+\infty).$ Решение
34. (Т/Р А. Ларина) Решите неравенство
$log_{9x}27\leq \frac{1}{log_3x}.$
Ответ: $(0;\frac{1}{9})\cup(1;3].$ Решение
35. (Т/Р А. Ларина) Решите неравенство
$\large\frac{7-71\cdot 3^{-x}}{3^x+10\cdot 3^{-x}-11}\leq 1$.
Ответ: $(-\infty;0)\cup${$2$}$\cup (log_310;+\infty).$ Решение
36. (Т/Р А. Ларина) Решите неравенство
$log_x512\leq log_2\frac{64}{x}.$
Ответ: $(0;1)\cup${$8$}. Решение
37. (Т/Р А. Ларина) Решите неравенство
$x\sqrt x+2\sqrt x+3\leq \frac{6}{2-\sqrt x}.$
Ответ: {$0$}$\cup [1;4).$ Решение
38. (Т/Р А. Ларина) Решите неравенство
$log_x(11x-2x^2)+log_{11-2x}x^4\leq 5.$
Ответ: $(0;1)\cup ${$-1+2\sqrt3$}$(5;5,5).$ Решение
39. (Т/Р А. Ларина) Решите неравенство
$\frac{log_{(-36x)}6^{x+2}}{log_{36}6^{x+2}}\leq log_{x^2}36.$
Ответ: $[-36;-2)\cup (-2;-1)\cup (-\frac{1}{36};0).$ Решение
40. (Т/Р А. Ларина) Решите неравенство
$log^2_2\frac{x-5}{x+2}-log_2(x-5)^2\cdot log_{(x-5)^2}\frac{x-5}{x+2}\geq 0$.
Ответ: $[-9;-2)\cup (5;6)\cup (6;+\infty).$ Решение
41. (Т/Р А. Ларина) Решите неравенство
$log_x(1-2x)\leq 3-log_{(\frac{1}{x}-2)}x.$
Ответ: $(0;\frac{1}{3})\cup${$\sqrt2-1$}. Решение
42. (Т/Р А. Ларина) Решите неравенство
$log_3(x+1,5)-log_{\sqrt2}(3,5-x)+log_{x+1,5}3\cdot log_2^2(3,5-x)\leq 0.$
Ответ: $(-1,5;-0,5)\cup $ {$1,5$}. Решение
43. (Т/Р А. Ларина) Решите неравенство
$\frac{log_{3-x}\sqrt x}{1-log_{x^2}(3-x)}\leq 1.$
Ответ: $(0;1)\cup (1;\frac{\sqrt{13}-1}{2})\cup${$1,5$}$\cup(2;3).$ Решение
44. (Т/Р А. Ларина) Решите неравенство
$|6-7^x|\leq (7^x-6)\cdot log_6(x+1).$
Ответ: $(-1;-\frac{5}{6}]\cup${$log_76$}$[5;+\infty)$. Решение
45. (Т/Р А. Ларина) Решите неравенство
$(x+3)(x+1)+3(x+3)\sqrt{\frac{x+1}{x+3}}+2\leq 0.$
Ответ: $[-2-\sqrt5;-2-\sqrt2].$ Решение
46. (Т/Р А. Ларина) Решите неравенство
$log_{5-x}(5+9x-2x^2)+log_{1+2x}(x^2-10x+25)^2\leq 5.$
Ответ: $(-0,5;0)\cup${$6-2\sqrt3$}$\cup (4;5).$ Решение
47. (Т/Р А. Ларина) Решите неравенство
$log_2(x^2-8x+6)\geq 2+\frac{1}{2}log_2(2x-1).$
Ответ: $(\frac{1}{2};2-\sqrt2]\cup [6+\sqrt{10};+\infty).$ Решение
48. (Т/Р А. Ларина) Решите неравенство
$\frac{\sqrt{2x-1}+\sqrt{x-3}-3x+10}{\sqrt{2x^2-7x+3}}>2$.
Ответ: $(3;25-6\sqrt{13}).$ Решение
49. (Т/Р А. Ларина) Решите неравенство
$\frac{6-3x+\sqrt{2x^2-5x+2}}{3x-\sqrt{2x^2-5x+2}}\geq \frac{1-x}{x}.$
Ответ: $[-1;0)\cup (\frac{2}{7};\frac{1}{2}]\cup [2;+\infty).$ Решение
50. (Т/Р А. Ларина) Решите неравенство
$log_{4x}2x-log_{2x^2}4x^2\geq -\frac{3}{2}.$
Ответ: $(0;\frac{1}{4})\cup [\frac{1}{\sqrt8};\frac{1}{\sqrt2})\cup [1;+\infty).$ Решение
51. (Т/Р А. Ларина) Решите неравенство
$\large\frac{log_2(2\cdot 4^x-11\cdot 2^x+9)}{x+3}\leq 1.$
Ответ: $(-\infty;-3)\cup [-1;0)\cup (2log_23-1;2log_23].$ Решение
52. (Т/Р А. Ларина) Решите неравенство
$log_x(3-x)log_x(4-x)-log_x(x^2-7x+12)+1\geq 0.$
Ответ: $(0;1)\cup (1;1,5]\cup [2;3).$ Решение
53. (Т/Р А. Ларина) Решите неравенство
$\large\frac{\sqrt{6+x-x^2}}{log_2(5-2x)}\leq \frac{\sqrt{6+x-x^2}}{log_2(x+4)}.$
Ответ: $[-2;\frac{1}{3}]\cup (2;2,5).$ Решение
54. (Т/Р А. Ларина) Решите неравенство
$log_3(x^2-4x+5)\leq \frac{2x}{log_{x^2-4x+5}(9^x+3^x-12)}.$
Ответ: $(log_3\frac{-1+\sqrt{53}}{2};2)\cup (2;log_312].$ Решение
55. (Т/Р А. Ларина) Решите неравенство
$log_x(\frac{100}{x})\leq \sqrt{log_x(100x^5)}$.
Ответ: $(0;\frac{1}{\sqrt[5]100}]\cup [\sqrt{10};+\infty).$ Решение
56. (Т/Р А. Ларина) Решите неравенство
$log_{2x^2-x}(3x-1)\cdot log_{2x-x^2}(3-2x)\geq 0.$
Ответ: $ [\frac{2}{3};1)\cup (1;1,5).$ Решение
57. (Т/Р А. Ларина) Решите неравенство
$log_{2x}(x-4)log_{x-1}(6-x)<0.$
Ответ: $(4;5)\cup (5;6).$ Решение
58. (Т/Р А. Ларина) Решите неравенство
$log_3(x+6)\leq (1-log_{9x}(6-x))\cdot log_3(9x).$
Ответ: $[3;6).$ Решение
59. (Т/Р А. Ларина) Решите неравенство
$\sqrt{1-log_5(x^2-2x+2)}<\frac{1}{2}log_{\sqrt5}(5x^2-10x+10).$
Ответ: $[-1;1)\cup (1;3].$ Решение
60. (Т/Р А. Ларина) Решите неравенство
$log_xlog_2(3-4^{x-1})\leq 1.$
Ответ: $(0;1)\cup (1;1,5).$ Решение
61. (Т/Р А. Ларина) Решите неравенство
$\large\frac{log_5(x^2-4x-11)^2-log_{11}(x^2-4x-11)^3}{2-5x-3x^2}\geq 0.$
Ответ: $(-\infty;-2)\cup (-2;2-\sqrt{15})\cup [6;+\infty).$ Решение
62. (Т/Р А. Ларина) Решите неравенство
$\large\frac{log_{2^{x+3}}4}{log_{2^{x+3}}(-4x)}\leq \frac{1}{log_2(log_{\frac{1}{2}}2^x)}.$
Ответ: $[-4;-3)\cup (-3;-1)\cup (-\frac{1}{4};0).$ Решение
63. (Т/Р А. Ларина) Решите неравенство
$log_x(1-2x)\leq 3-log _{\frac{1}{x}-2}x.$
Ответ: $(0;\frac{1}{3})\cup${$-1+\sqrt2$}. Решение
64. (Т/Р А. Ларина) Решите неравенство
$log_2(5-x)\cdot log_{x+1}\frac{1}{8}\geq -6.$
Ответ: $(-1;0)\cup [1;5).$ Решение
65. (Т/Р А. Ларина) Решите неравенство
$\frac{log_712}{log_7(x^2-9)}\geq \frac{log_5(x^2+8x+12)}{log_5(x^2-9)}.$
Ответ: $[-8;-6)\cup (3;\sqrt{10}).$ Решение
66. (Т/Р А. Ларина) Решите неравенство
$4log_2x+log_2\frac{x^2}{8(x-1)}\leq 4-\log_2(x-1)-log^2_2x.$
Ответ: ($1;2$]. Решение
67. (Т/Р А. Ларина) Решите неравенство
$\sqrt{1-log_5(x^2-2x+2)}<log_5(5x^2-10x+10).$
Ответ: [$-1;1$)$\cup$($1;3$]. Решение
68. (Т/Р А. Ларина) Решите неравенство
$\large log_{\frac{x^2-18x+91}{90}}(5x-\frac{3}{10})\leq0.$
Ответ: [$\frac{13}{50};9+4\sqrt5$). Решение
69. (Т/Р А. Ларина) Решите неравенство
$log_{cosx^2}(\frac{3}{x}-2x)<log_{cosx^2}(2x-1).$
Ответ: $(\frac{1}{2};1).$ Решение
70. (Т/Р А. Ларина) Решите систему неравенств
$\begin{cases}log_2(5-x)(2-x)>log_4(x-2)^2,\\\frac{2^x-2^{2-x}-3}{2^x-2}\geq 0;&\end{cases}$
Ответ: $(-\infty;1)\cup(6;+\infty).$ Решение
71. (Т/Р А. Ларина) Решите систему неравенств
$\begin{cases}4^{x+1}-33\cdot 2^x+8\leq 0,\\2log_2\frac{x-1}{x+1,3}+log_2(x+1,3)^2\geq 2;&\end{cases}$
Ответ: [spoiler]{$-4$}$\cup (3,7;4]$ Решение
72. (Т/Р А. Ларина) Решите систему неравенств
$\begin{cases}\frac{|x-5|-1}{2|x-6|-4}\leq 1,\\\frac{1}{4}log_2(x-2)-\frac{1}{2}\leq log_{\frac{1}{4}}\sqrt{x-5};&\end{cases}$
Ответ: $(5;6].$ Решение
73. (Т/Р А. Ларина) Решите неравенство
$\frac{x^2-x+1}{x-1}+\frac{x^2-3x-1}{x-3}\leq 2x+2.$
Ответ: $(-\infty;1)\cup${$2$}$\cup (3;+\infty).$ Решение
74. (Т/Р А. Ларина) Решите неравенство
$\frac{2^{cosx}-1}{3\cdot 2^{cosx}-1}\leq 2^{1+cosx}-2.$
Ответ: $[-\frac{\pi}{2}+2\pi n;\frac{\pi}{2}+2\pi n]\cup${$\pi+2\pi n$}, $n\in Z.$ Решение
75. (Т/Р А. Ларина) Решите неравенство
$\frac{5(x-6\sqrt x+8)}{x-16}\leq \sqrt x-2.$
Ответ: $[0;1]\cup [4;16)\cup (16;+\infty).$ Решение
76. (Т/Р А. Ларина) Решите неравенство
$\frac{2^{x+1}\sqrt{2^{x+1}-1}}{2^x-15}\leq \frac{\sqrt{2^{x+1}-1}}{2^x-8}.$
Ответ: {$-1$}$\cup [0;log_215-1]\cup (3;log_215).$ Решение
77. (Т/Р А. Ларина) Решите неравенство
$\frac{4^{x}-3\cdot 2^x+3}{2^x-2}+\frac{4^{x}-5\cdot 2^x+3}{2^x-4}\leq 2^{x+1}.$
Ответ: $(-\infty;1)\cup${$log_23$}$\cup (2;+\infty).$ Решение
78. (Т/Р А. Ларина) Решите неравенство
$log_{6x-x^2-8}(5-x)\geq log_{6x-x^2-8}(4x^2-17x+20).$
Ответ: $[2,5;3)\cup (3;4).$ Решение
79. (Т/Р А. Ларина) Найдите область определения функции $y=\sqrt{1-\frac{2^{x+1}-14}{4^x-2^{x+2}-5}}.$
Ответ: {$log_23$}$\cup (log_25;+\infty).$ Решение
80. (Т/Р А. Ларина) Решите неравенство $\large|3^{x+1}-9^x|+|9^x-5\cdot 3^x+6|\leq 6-2\cdot 3^x.$
Ответ: $(-\infty;log_32)\cup ${$1$}. Решение
81. (Т/Р А. Ларина) Решите неравенство $\large\frac{9}{3+log_3x\cdot log_3\frac{9}{x}}\leq log_3^2x-log_3\frac{x^2}{27}.$
Ответ: $(0;\frac{1}{3})\cup ${$1;9$}$\cup (27;+\infty).$ Решение
82. (Т/Р А. Ларина) Решите неравенство $\frac{8^x-3\cdot 2^{2x+1}+2^{x+3}+1}{4^x-3\cdot 2^{x+1}+8}\geq 2^x-1.$
Ответ: $(-\infty;1)\cup${$log_23$}$\cup (2;+\infty).$ Решение
83. (Т/Р А. Ларина) Решите неравенство $\large\frac{(2^x-2)^3}{2^{x+2}-12}\geq \frac{8^x-4^{x+1}+2^{x+2}}{9-4^x}.$
Ответ: $(-\infty;0]\cup ${$1$}$\cup (log_23;+\infty).$ Решение
84. (Т/Р А. Ларина) Решите неравенство $\sqrt{4\sqrt3 sin\frac{\pi x}{3}-4sin^2\frac{\pi x}{3}-3}\cdot (log_{\frac{2}{3}}\frac{3x+22}{14-x})\leq 0.$
Ответ: {$-5;-4;1;2;7;8;13$}. Решение
85. (Т/Р, 2017) Решите неравенство $3^{|x|}-8-\frac{3^{|x|}+9}{9^{|x|}-4\cdot 3^{|x|}+3}\leq \frac{5}{3^{|x|}-1}.$
Ответ: $[-2;-1)\cup [-log_32;0)\cup (0;log_32]\cup (1;2].$ Решение
86. (Т/Р А. Ларина) Решите неравенство
$\large\frac{\sqrt{(x-1)(x-2)log_{x^2}\frac{2}{x^2}}}{|x+2|}>\frac{x^2-3x+1+log_{|x|}\sqrt2}{x+2}.$
Ответ: $[\sqrt2;2].$ Решение
87. (Т/Р А. Ларина) Решите неравенство
$3\sqrt{x^2+6x+9}-(\sqrt{3x+7})^2-2|x-1|\leq 0.$
Ответ: $[-\frac{7}{3};0]\cup[2;+\infty).$ Решение
88. (Т/Р А. Ларина) Решите неравенство
$2^{1+2x-x^2}-3\geq \frac{3}{2^{2x-x^2}-2}.$
Ответ: $[1-\sqrt2;1)\cup (1;1+\sqrt2].$ Решение
89. (Т/Р А. Ларина) Решите неравенство
$\frac{log_2(|x|-1)log_2(\frac{|x|-1}{16})+3}{\sqrt{log_2(7-|x+4|)}}\geq 0.$
Ответ: $(-10;-9]\cup[-3;-1)\cup (1;2).$ Решение
90. (Т/Р А. Ларина) Решите неравенство
$\large\frac{4^{\sqrt{x-1}}-5\cdot 2^{\sqrt{x-1}}+4}{log^2_2(7-x)}\geq 0.$
Ответ: {$1$}$\cup [5;6)\cup (6;7).$ Решение
91. (Т/Р А. Ларина) Решите неравенство
$\frac{2^{x+1}-7}{4^x-2^{x+1}-3}\leq 1.$
Ответ: {$1$}$\cup (log_23;+\infty).$ Решение
92. (Т/Р А. Ларина) Решите неравенство
$\frac{5-7log_x3}{log_3x-log_x3}\geq 1.$
Ответ: $(\frac{1}{3};1)\cup(1;3)\cup [9;27].$ Решение
93. (Т/Р А. Ларина) Решите неравенство
$\frac{x+6\sqrt x+28}{120}\leq \frac{2-\sqrt x}{x-6\sqrt x+8}.$
Ответ: $[0;4)\cup (4;16).$ Решение
94. (Т/Р А. Ларина) Решите неравенство
$\frac{9}{log_2(4x)}\leq 4-log_2x.$
Ответ: $(0;0,25)\cup \left \{ 2 \right \}.$ Решение
95. (Т/Р А. Ларина) Решите неравенство
$\frac{1}{log_3(2x-1)\cdot log_{x-1}9}< \frac{log_3\sqrt{2x-1}}{log_3(x-1)}.$
Ответ: $(1;1,5)\cup (2;+\infty).$ Решение
96. (Т/Р А. Ларина) Решите неравенство
$log_{\frac{5-x}{4}}(x-2)\cdot log_{x-2}(6x-x^2)\geq log_{\frac{5-x}{4}}(3x^2-10x+15).$
Ответ: $[2,5;3)\cup (3;5).$ Решение
97. (Т/Р А. Ларина) Решите неравенство
$log_3(2^x+1)+log_{2^x+1}3\geq 2,5.$
Ответ: $(-\infty;log_2(\sqrt3-1)]\cup [3;+\infty).$ Решение
98. (Т/Р А. Ларина) Решите неравенство
$\frac{83-17\cdot 2^{x+1}}{4^x-2^{x+2}+3}\leq 4^x+3\cdot 2^{x+1}+17.$
Ответ: $[0;1,5)\cup(log_23;+\infty).$ Решение
99. (Т/Р А. Ларина) Решите неравенство
$xlog_2\frac{x}{2}+log_x4\leq 2.$
Ответ: $(0;1)\cup$ {$2$}. Решение
100. (Т/Р А. Ларина) Решите неравенство
$(3^x-2^x)(6^{x+1}+1)+6^x\geq 3^{2x+1}-2^{2x+1}.$
Ответ: {$-1$}$\cup [0;+\infty).$ Решение
101. (Т/Р А. Ларина) Решите неравенство
$2\sqrt{sin^2x-sinx-1}\geq cos^2x+sinx+3.$
Ответ: $-\frac{\pi}{2}+2\pi n,n\in Z.$ Решение
102. (Т/Р А. Ларина) Решите неравенство
$\large\frac{log_8x}{log_2(1+2x)}\leq \frac{log_2\sqrt[3]{1+2x}}{log_2x}.$
Ответ: $(0;0,5]\cup (1;+\infty).$ Решение
103. (Т/Р А. Ларина) Решите неравенство
$-3log_{(x-1)}\frac{1}{3}+log_{\frac{1}{3}}(x-1)>2|log_{\frac{1}{3}}(x-1)|.$
Ответ: $(2;4).$ Решение
104. (Т/Р 283 А. Ларина) Решите неравенство
$log_{\sqrt3-1}(9^{|x|}-2\cdot 3^{|x|})\leq log_{\sqrt3-1}(2\cdot 3^{|x|-3}.$
Ответ: $(-\infty;-1]\cup [1;+\infty)$ Видеорешение