Тренировочный вариант №126 А. Ларина

а)

$5\cdot (\frac{1}{5})^{cos2x}=5^{sin2x};$

$(\frac{1}{5})^{cos2x-1}=(\frac{1}{5})^{-sin2x};$

$cos2x-1=-sin2x;$

$(cos^2x-sin^2x)-(cos^2x+sin^2x)=-2sinx\cdot cosx;$

$sin^2x=sinx\cdot cosx;$

$sinx(sinx-cosx)=0;$

$sinx=0$ или $sinx=cosx;$

$x=\pi n$ или $x=\frac{\pi}{4}+\pi k, n,k\in Z.$

б)  Отбор корней производим при помощи тригонометрического круга.

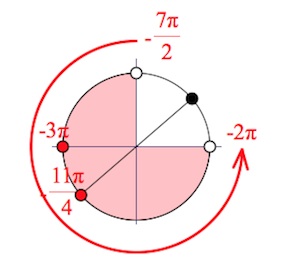
Ответ:

а) $\pi n,\frac{\pi}{4}+\pi k, n,k\in Z;$

б) $-3\pi;-\frac{11\pi}{4}.$

a) Пусть $KC$ пересекается с $BD$ в точке $N$.

Треугольники $BCN,DKN$ подобны, $k=\frac{BC}{KD}=\frac{6}{3}=2$. Откуда и $BN:ND=2:1$ (или $\frac{DB}{DN}=3:1$).

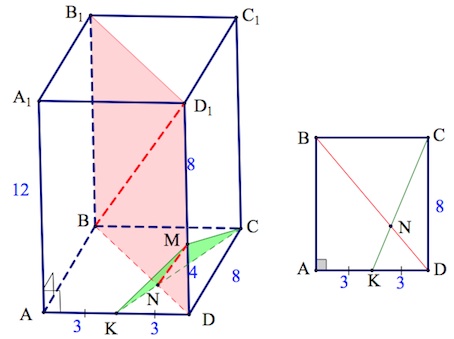
Замечаем, треугольники $DBD_1, DNM$ подобны по двум пропорциональным сторонам ($\frac{DB}{DN}=\frac{DD_1}{DM}=3:1$) и углу между ними ($\angle D$ – общий для треугольников).

А значит, равны углы $DBD_1,DNM$ (а они соответственные при прямых $NM,BD_1$ и секущей $BD$), то есть прямые $NM,BD_1$ параллельны по признаку параллельности прямых.

Итак, в плоскости $CKM$ нашлась прямая ($NM$),параллельная $BD_1$, а значит, прямая $BD_1$ параллельна плоскости $CKM$ по признаку параллельности прямой и плоскости.

Что и требовалось доказать.

б) Пусть $DH\perp CK$ ($H\in CK$). По теореме о трех перпендикулярах и  $MH\perp CK$. Тогда $\angle (CKM;ABC)=\angle MHD.$

$S_{CKM}=\frac{S_{CKD}}{cos MHD}$ (треугольник $CKD$ – проекция $CKM$ на $ABC$)

Для треугольника $CKD$

$HD\cdot CK=KD\cdot CD;$

$HD=\frac{3\cdot 8}{\sqrt{3^2+8^2}};$

$HD=\frac{24}{\sqrt{73}}.$

Из треугольника $MHD$

$cos MHD=\frac{HD}{HM}=\frac{HD}{\sqrt{HD^2+DM^2}}=\frac{\frac{24}{\sqrt{73}}}{\frac{\sqrt{1744}}{\sqrt{73}}}=\frac{6}{\sqrt{109}}.$

Далее, $S_{CKD}=12$.

Наконец, $S_{CKM}=\frac{12}{\frac{6}{\sqrt{109}}}=2\sqrt{109}.$

Ответ: б) $2\sqrt{109}.$

 $log_{(x-2)^2}\frac{5-x}{4-x}\leq 1+log_{(x-2)^2}\frac{1}{(x-5)(x-4)};$

$log_{(x-2)^2}\frac{x-5}{x-4}-log_{(x-2)^2}\frac{1}{(x-5)(x-4)}\leq 1;$

$\begin{cases}log_{(x-2)^2}(x-5)^2\leq 1,\\(x-4)(x-5)>0;&\end{cases}$

$\begin{cases}log_{(x-2)^2}(x-5)^2\leq log _{(x-2)^2}(x-2)^2,\\(x-4)(x-5)>0;&\end{cases}$

Применяем метод замены множителей к первой строке системы (заменяем разность $log_{(x-2)^2}(x-5)^2-log _{(x-2)^2}(x-2)^2$ на разность $((x-2)^2-1)((x-5)^2-(x-2)^2)$ при условии $(x-2)^2>0, (x-2)^2\neq 1$, ограничения на подлогарифмные выражения уже указаны в системе).

$\begin{cases}((x-2)^2-1)((x-5)^2-(x-2)^2)\leq 0,\\(x-2)^2>0,\\(x-2)^2\neq 1,\\(x-4)(x-5)>0;&\end{cases}$
$\begin{cases}-(x-3)(x-1)(2x-7)\leq 0,\\x\neq 2,\\x\neq 3,\\x\neq 1,\\(x-4)(x-5)>0;&\end{cases}$

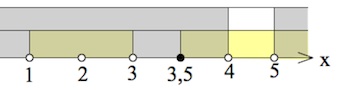
$x\in (1;2)\cup (2;3)\cup [3,5;4)\cup (5;+\infty).$

Ответ: $(1;2)\cup (2;3)\cup [3,5;4)\cup (5;+\infty).$

а) Продлим за точку $M$ отрезок $DM$, обозначив точку пересечения образовавшегося луча с окружностью за $P$.

Пусть $H_1, H_2$ – основания перпендикуляров, проведенных из центра окружности к сторонам $CM,PM.$

По условию углы $CMA, DMB$ равны, а поскольку углы $AMP,DMB$ – вертикальные, то $\angle CMA=\angle PMA$, то есть $MA$ – биссектриса угла $CMP.$

По свойству биссектрисы угла $OH_1=OH_2$. Тогда треугольники $ODH_2,OCH_1$ равны по гипотенузе и катету. Откуда и вытекает равенство соответствующих углов, а именно $\angle OCM=\angle ODM.$

Что и требовалось доказать.

б) Пусть $\angle OCM=\angle ODM=\varphi $.

Поскольку $\angle CMD=90^{\circ}$, то угол $DKM$ ($K$ – точка пересечения $OD$ и $CM$) есть $90^{\circ}-\varphi $.

Но тогда в треугольнике $COK$  $\angle COK=90^{\circ}$.

Итак, разобьем четырехугольник $COMD$ на треугольники $COD$ (прямоугольный) и $ODM$. 

$S_{COD}=\frac{CO\cdot OD}{2}=\frac{6^2}{2}=18.$

$S_{ODM}=\frac{OM\cdot MD\cdot sin OMD}{2}.$

Нам потребуется $MD$, длину которой найдем по теореме косинусов из треугольника $ODM:$

$OD^2=OM^2+MD^2-2OM\cdot MD\cdot cos135^{\circ};$

$6^2=4^2+MD^2+8\cdot MD\cdot \frac{\sqrt2}{2};$

$MD^2+4\sqrt2MD-20=0;$

$MD=-2\sqrt2+2\sqrt{7};$

Тогда $S_{ODM}=\frac{4\cdot (2\sqrt7-2\sqrt2)\cdot \frac{\sqrt2}{2}}{2}=2\sqrt{14}-4.$

Итак, $S_{COMD}=18+2\sqrt{14}-4=14+2\sqrt{14}.$

Ответ: б) $14+2\sqrt{14}.$

Пусть скорость течения – $x$ км/час, собственная cкорость лодки – $y$ км/час.

За 5 часов (с 6 до 11 утра) плот, выйдя из А, проплывет (до встречи с лодкой) $5x$ км, лодка пройдет, выйдя из В, (против течения, до встречи с плотом) $5(y-x)$ км.

Стало быть, расстояние между городами А и В – $5y$ км.

Лодка доплывает от места встречи до А за $\frac{5x}{(y-x)}$ часов.

Далее лодка доплывет от А до В (по течению) за $\frac{5y}{y+x}$ часов.

Плот доходит до В (от места встречи с лодкой) за $\frac{5(y-x)}{x}$ часов.

Так как доплыв до города А, лодка сразу же повернула обратно и приплыла в город В одновременно с плотом, то

$\frac{5x}{y-x}+\frac{5y}{y+x}=\frac{5(y-x)}{x};$

$\frac{x}{y-x}+\frac{y}{y+x}=\frac{(y-x)}{x};$

$x^2(x+y)+xy(y-x)=(y-x)^2(x+y);$

$x^3+x^2y+xy^2-x^2y= x^3+x^2y-2x^2y-2xy^2+xy^2+y^3;$

$xy^2=-x^2y-xy^2+y^3;$

$2xy^2+x^2y-y^3=0;$

$y(2xy+x^2-y^2)=0;$

$2xy+x^2-y^2=0;$

$(\frac{y}{x})^2-2(\frac{y}{x})-1=0;$

$\frac{y}{x}=1+\sqrt 2;$

Чтобы лодка и плот успели прибыть в город В к 6 ч вечера того же дня, необходимо:

$\frac{5(y-x)}{x}\leq 7;$

$\frac{5y}{x}-5\leq 7;$

Мы же имеем:

$5+5\sqrt 2-5\leq 7;$

$5\sqrt 2\leq 7;$

$\sqrt{50}\leq \sqrt{49}$, что неверно.

Неравенство не выполняется, стало быть, лодка и плот не успели прибыть в город В к 6 ч вечера того же дня.

Ответ: нет.

При $x\geq 0$ $f'(x)=3x^2-6ax+3a^2-3.$

При $x<0$ $f'(x)=3x^2-6ax+3a^2+3.$

Заметим, при $x<0$  $f'(x)=3x^2-6ax+3a^2+3=3(x-a)^2+3>0$, то есть  $f(x)$ не имеет экстремумов на $(-\infty;0)$ (в частности, на $(-2;0)$).

Тогда остается потребовать, чтобы $f(x)$ имело бы два экстремума на $[0;3)$.

Заметим, при $x\geq 0$  $f'(x)=0$ при $x=a\pm 1.$

Возможны два случая.

1) $x=0$ – одна из точек экстремума. Тогда на $(0;3)$ должна существовать еще одна точка экстремума.

2) $x=0$ – не точка экстремума. Тогда на $(0;3)$ должны существовать две точки экстремума.

В первом случае $f'(0)\leq 0$ и $0<a+1<3.$ То есть получаем, что $-1<a\leq 1.$

Во втором случае

$f'(0)>0$ и $0<a+1<3$ и $0<a-1<3$. То есть получаем, что $1< a<2.$

Итак, объединяя оба случая, приходим к тому, что $-1<a<2.$

Ответ: $(-1;2).$