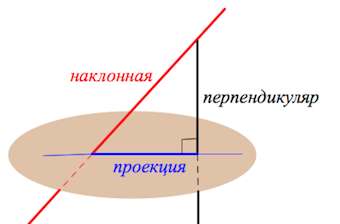
Перпендикуляр и наклонная

Перпендикуляр короче любой наклонной, проведенной к плоскости из той же точки

У равных наклонных, проведенных к плоскости из одной точки, проекции равны. Верно и обратное. Если равны проекции наклонных к плоскости, проведенных из одной точки, то равны и наклонные.

Из двух наклонных, проведенных к плоскости из одной точки, больше та, у которой проекция больше.

Верно и обратное.

Теорема о трех перпендикулярах

Если прямая, лежащая в плоскости и проходящая через основание наклонной, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной.

Если прямая, лежащая в плоскости и проходящая через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Заметим, что, вообще говоря, теорема о трех перпендикулярах верна и в более общем случае:

Если прямая, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной. И наоборот.