Подготовка к ЕГЭ по математике

Найдите все значения а, при каждом из которых уравнение $\sqrt{x-a}\cdot sin x=\sqrt{x-a}\cdot cos x$ имеет ровно один корень на отрезке $[0;\pi]. $

Решение:

$\sqrt{x-a}\cdot sin x=\sqrt{x-a}\cdot cos x;$

$\sqrt{x-a}\cdot (sin x- cos x)=0;$

$\left[\begin{array}{rcl}x=a,\\\begin{cases}sinx=cosx,\\x-a\geq 0;\end{cases};\end{array}\right.$

$\left[\begin{array}{rcl}x=a,\\\begin{cases}x=\frac{\pi}{4}+\pi n,n\in Z,\\x-a\geq 0;\end{cases};\end{array}\right.$

С учетом условия $x\in [0;\pi]$ имеем:

$\left[\begin{array}{rcl}a=x,\\\begin{cases}x=\frac{\pi}{4},\\a\leq x;\end{cases};\end{array}\right.$

Становится видно, что исходное уравнение имеет ровно один корень на отрезке $[0;\pi]$ при $a\in (-\infty;0)\cup [\frac{\pi}{4};\pi].$

Ответ: $(-\infty;0)\cup [\frac{\pi}{4};\pi].$

Задание 15 ЕГЭ 2023

В июле 2025 года планируется взять кредит в банке на некоторую сумму на 10 лет. Условия его возврата таковы:

• каждый январь долг увеличивается на $10$% по сравнению с концом предыдущего года;
• с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
• в июле каждого из годов с 2026 по 2030 долг уменьшается на одну и ту же сумму по сравнению с июлем предыдущего года;
• в июле каждого из годов с 2031 по 2035 долг уменышается на одну и ту же сумму по сравнению с июлем предыдущего года, отличную от суммы, на которую долг убывал в первые пять лет.

Известно, что в конце 2030 года долг составил $800$ тысяч рублей. Найдите начальную сумму кредита, если сумма выплат по кредиту равна $2090$ тысяч рублей.

Решение:

(Реальный ЕГЭ 2023)

Решите неравенство: $\large \frac{log_2x^2-log_3x^2}{log_6^2(2x^2-10x+12,5)+1}\geq 0$

Решение:

$\Large \frac{log_2x^2-log_3x^2}{log_6^2(2x^2-10x+12,5)+1}\geq 0;$

$\Large \frac{log_2x^2-\frac{log_2x^2}{log_23}}{log_6^2(2x^2-10x+12,5)+1}\geq 0;$

Заметим,  

$\large log_6^2(2x^2-10x+12,5)+1>0$ при $\large 2x^2-10x+12,5>0.$

Тогда

$\large log_2x^2-\frac{log_2x^2}{log_23}\geq 0$ при условии $\large 4x^2-20x+25>0;$  

$\large log_2x^2\cdot (1-log_23)\geq 0$ при условии $\large (2x-5)^2>0;$

$\large log_2x^2\cdot (log_33-log_23)\geq 0$ при условии $\large x\neq 2,5;$

$\large log_2x^2\cdot log_31,5\geq 0$ при условии $\large x\neq 2,5;$

Заметим, $\large log_31,5>log_31=0.$

$\large log_2x^2\geq 0,$ $\large x\neq 2,5.$

Используем метод рационализации:

$\large (2-1)(x^2-1)\geq 0,$ $\large x\neq 2,5,x^2>0;$

$\large (x-1)(x+1)\geq 0,$ $\large x\neq 2,5,x\neq 0;$

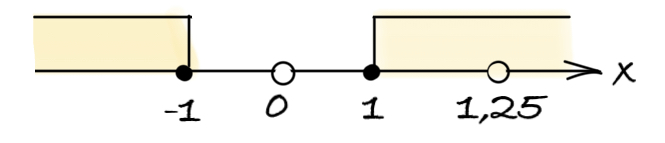
$\large x\in (-\infty;-1]\cup [1;1,25)\cup (1,25;+\infty).$

Ответ: $\large (-\infty;-1]\cup [1;1,25)\cup (1,25;+\infty).$

№ 13. а) Решите уравнение $4cos^3x-2\sqrt3 cos2x+3cosx=2\sqrt3;$
б) Укажите корни этого уравнения, принадлежащие отрезку $[2\pi; 3,5\pi].$

Решение: [spoiler]

Смотрите также №13 и №15 Т/Р №283 А. Ларина

18. Найдите все значения параметра $a,$ при каждом из которых уравнение

$log_{3x-4}(a+9x+5)=-1$

имеет единственный корень на промежутке $(\frac{4}{3};2].$
Читать далее

Смотрите также №16 Т/Р №280

16. Плоскость $\alpha $ пендикулярна основанию правильной треугольной пирамиды  $SABC$ и делит стороны $AB$   и  $BC$   основания пополам.

а) Докажите, что плоскость $\alpha $ делит боковое ребро в отношении $1:3$, считая от вершины $S$.

б) Найдите отношение объемов многогранников, на которые плоскость $\alpha $ разбивает пирамиду. Читать далее

[latexpage]Равносильность

Равносильными или эквивалентными называются уравнения (неравенства), множества корней которых совпадают. Равносильными также считаются уравнения (неравенства), которые не имеют корней. Читать далее

Смотрите также задания №1-12; №13; №14; №15; №17; №18; №19

16. В треугольнике $ABC$ угол $ABC$ тупой, $H$ — точка пересечения продолжений высот, угол $AHC$ равен $60$°.
а) Докажите, что угол $ABC$ равен $120$°.
б) Найдите $BH$, если $AB= 7, BC = 8.$

Читать далее