ЕГЭ 2023, резерв
В основании четырехугольной пирамиды SABCD лежит прямоугольник ABCD. На ребрах SA, SB, SC и SD отмечены точки L, K, N и M соответственно так, что четырехугольник KLMN — трапеция с основанием KL = 3 и MN = 2. Известно, что $SK:KB=3:1.$
а) Докажите, что плоскость KLM пересекает ребра SC и SD в их серединах.
б) Найдите высоту SH пирамиды, если точка пересечения диагоналей пирамиды совпадает с точкой H, площадь основания равна 24, а площадь сечения KLMN = 10.
Решение:

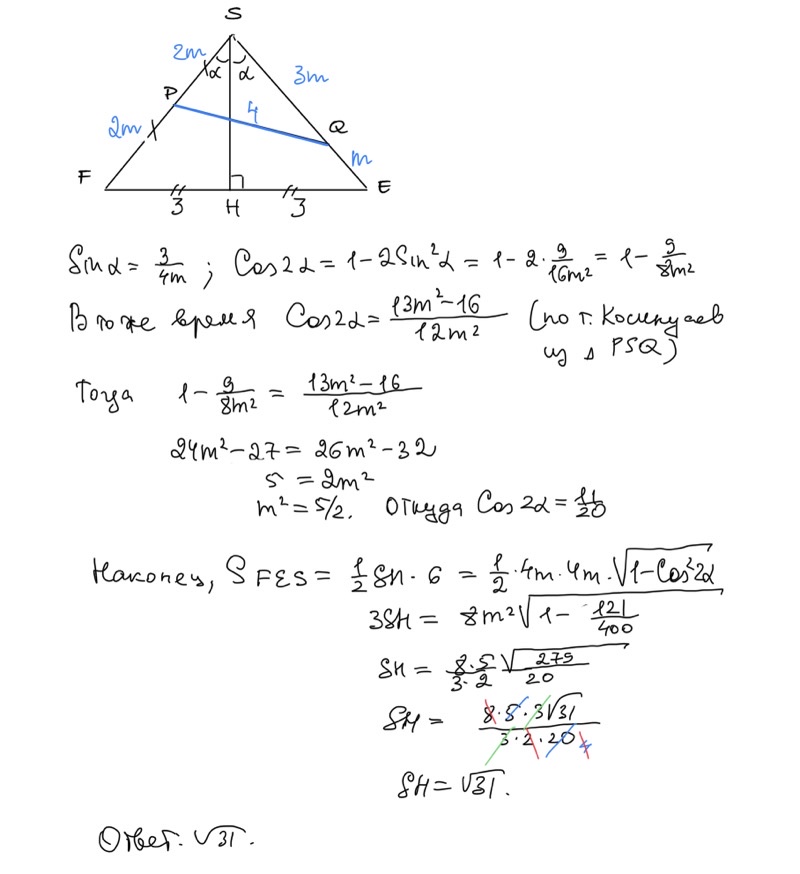


Добавить комментарий