Главная › 10 Графики функций › 10. Линейная функция
11 Янв 2022
Категория: 10 Графики функций

10. Линейная функция

2022-09-13

Задача 1. На рисунке изображён график функции y=kx+b.  Найдите y(-9).

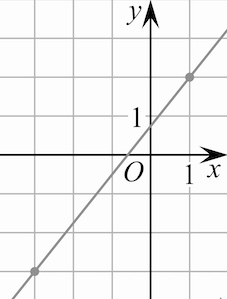
Решение: + показать

Задача 2. На рисунке изображён график функции f(x)=kx+b.   Найдите значение x, при котором f(x)=2,25. 

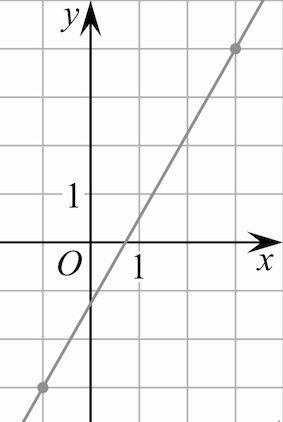
Решение: + показать

Задача 3.  На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.

Решение: + показать

Вы можете пройти тест “Линейная функция”
Автор: egeMax | Нет комментариев
Печать страницы

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *




одиннадцать − 7 =

https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_bye.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_good.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_negative.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_scratch.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_wacko.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_yahoo.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_cool.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_heart.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_rose.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_smile.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_whistle3.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_yes.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_cry.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_mail.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_sad.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_unsure.gif 
https://egemaximum.ru/wp-content/plugins/wp-monalisa/icons/wpml_wink.gif