Главная
Справочник
Видеоуроки
Тесты
Статьи
Архив
Карта сайта
Контакты
Задача 1. На рисунке изображён график функции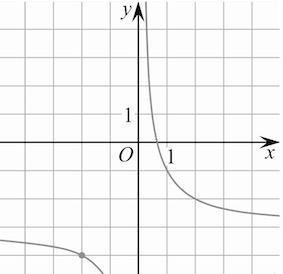 
Найдите 
Решение: + показать
и 
Задача 2. На рисунке изображён график функции вида 
где числа 
и 
— целые. Найдите значение 
, при котором 
Решение: + показать
– горизонтальная асимптота, значит 
– вертикальная асимптота, значит 
то
Задача 3. На рисунке изображён график функции вида где 
– целые числа. Найдите 
Решение: + показать
– горизонтальная асимптота, значит 
– вертикальная асимптота, значит 
Задача 4. На рисунке изображён график функции 
Найдите 
Решение: + показать
– горизонтальная асимптота, поэтому 
– вертикальная асимптота, поэтому 
Задача 5. На рисунке изображены графики функций 
и 
и которые пересекаются в точках 
и 
. Найдите ординату точки 
Решение: + показать
откуда
и 
или 
Вы можете пройти тест “Гиперболы”
Добавить комментарий