Задание 17 ЕГЭ 2023, досрок

Найдите все значения а, при каждом из которых уравнение $\sqrt{x-a}\cdot sin x=\sqrt{x-a}\cdot cos x$ имеет ровно один корень на отрезке $[0;\pi]. $

Решение:

$\sqrt{x-a}\cdot sin x=\sqrt{x-a}\cdot cos x;$

$\sqrt{x-a}\cdot (sin x- cos x)=0;$

$\left[\begin{array}{rcl}x=a,\\\begin{cases}sinx=cosx,\\x-a\geq 0;\end{cases};\end{array}\right.$

$\left[\begin{array}{rcl}x=a,\\\begin{cases}x=\frac{\pi}{4}+\pi n,n\in Z,\\x-a\geq 0;\end{cases};\end{array}\right.$

С учетом условия $x\in [0;\pi]$ имеем:

$\left[\begin{array}{rcl}a=x,\\\begin{cases}x=\frac{\pi}{4},\\a\leq x;\end{cases};\end{array}\right.$

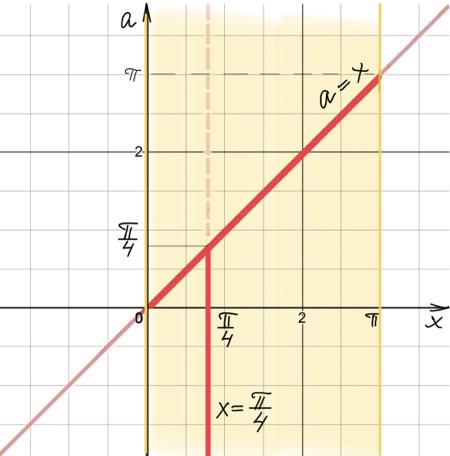
Становится видно, что исходное уравнение имеет ровно один корень на отрезке $[0;\pi]$ при $a\in (-\infty;0)\cup [\frac{\pi}{4};\pi].$

Ответ: $(-\infty;0)\cup [\frac{\pi}{4};\pi].$