Теорема Менелая

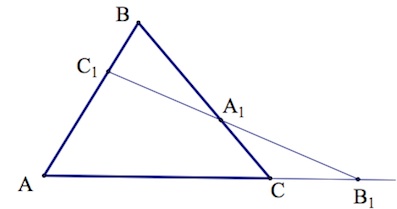
Если на сторонах $AB$ и $BC$ треугольника $ABC$ взяты соответственно точки $C_1$ и $A_1$, а точка $B_1$ взята на продолжении стороны $AC$ за точку $C$, то точки $C_1$, $A_1$ и $B_1$ лежат на одной прямой тогда и только тогда, когда выполнено равенство

$\frac{AC_1}{C_1B}\cdot \frac{BA_1}{A_1C}\cdot \frac{CB_1}{B_1A}=1.$

Доказательство:

=> Докажем прежде, что если точки $C_1$, $A_1$ и $B_1$ лежат на одной прямой, то выполняется равенство 

$\frac{AC_1}{C_1B}\cdot \frac{BA_1}{A_1C}\cdot \frac{CB_1}{B_1A}=1.$

Проведем через точку $C$ прямую, параллельную $AB$. Пусть она пересекается с прямой $C_1B_1$ в точке $D$.

Треугольники $A_1BC_1,A_1CD$ подобны по двум углам (см. рис), тогда

$\frac{BA_1}{CA_1}=\frac{C_1B}{DC}$  (1)

Треугольники $CDB_1,AC_1B_1$ подобны по двум углам (см. рис), тогда

$\frac{CB_1}{AB_1}=\frac{DC}{C_1A}$  (2)

Умножим (1) на (2), получим

$\frac{BA_1}{CA_1}\cdot \frac{CB_1}{AB_1}=\frac{C_1B}{DC}\cdot \frac{DC}{C_1A};$

$\frac{BA_1}{CA_1}\cdot \frac{CB_1}{AB_1}=\frac{C_1B}{C_1A}.$

Домножим обе части последнего равенства на $\frac{AC_1}{BC_1}:$

$\frac{AC_1}{BC_1}\cdot \frac{BA_1}{CA_1}\cdot \frac{CB_1}{AB_1}=1.$

<= Докажем теперь, что если выполняется равенство $\frac{AC_1}{C_1B}\cdot \frac{BA_1}{A_1C}\cdot \frac{CB_1}{B_1A}=1$, то точки $C_1$, $A_1$ и $B_1$ лежат на одной прямой.

Пусть прямая $A_1C_1$ пересекает прямую $AC$ в некоторой точке $B_2.$ Покажем, что $B_2=B_1.$

Для точек $C_1,A_1,B_2$, лежащих на одной прямой, выполняется равенство

$\frac{AC_1}{C_1B}\cdot \frac{BA_1}{A_1C}\cdot \frac{CB_2}{B_2A}=1$  (3)

А по условию выполняется и

$\frac{AC_1}{C_1B}\cdot \frac{BA_1}{A_1C}\cdot \frac{CB_1}{B_1A}=1$  (4)

 Разделим (3) на (4), получим

$\frac{CB_2}{B_2A}\cdot \frac{B_1A}{CB_1}=1$

или

$\frac{CB_2}{B_2A}=\frac{CB_1}{B_1A}.$

Откуда

$\frac{AB_2-AC}{B_2A}=\frac{AB_1-AC}{B_1A};$

$1-\frac{AC}{B_2A}=1-\frac{AC}{B_1A};$

$\frac{AC}{B_2A}=\frac{AC}{B_1A};$

$B_2A=B_1A$, то есть $B_2=B_1.$

Что и требовалось доказать.