Главная › Справочные материалы › Тригонометрический круг II

17 Мар 2013

Категория: Справочные материалы

Тригонометрический круг II

Елена Репина 2013-03-17 2021-06-18

Продолжение (начало здесь)

Перевод радиан в градусы и градусы в радианы

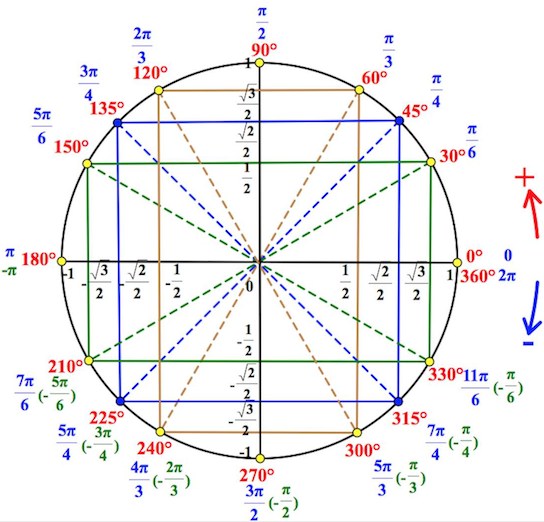
На тригонометрическом круге помимо углов в градусах мы наблюдаем радианы.

круг тригонометрический

Подробнее про радианы:+ показать

$\pi$ радиан – это $180^{\circ}.$

Так вот, например,

$\frac{\pi}{3}=\frac{180^{\circ}}{3}=60^{\circ}$ ,

$\frac{11\pi}{6}=\frac{11\cdot 180^{\circ}}{6}=330^{\circ}$ .

Так, мы научились переводить радианы в углы.

Теперь наоборот, давайте переводить градусы в радианы.

Допустим, нам надо перевести $80^{\circ}$ в радианы. Нам поможет пропорция. Поступаем следующим образом:

Так как, $180^{\circ}=\pi$ радиан, то заполним таблицу:

перевод градусов в радианы

Откуда

$x=\frac{80^{\circ}\cdot \pi}{180^{\circ}}=\frac{4\pi}{9}.$

Итак,

$80^{\circ}=\frac{4\pi}{9}.$

Тренируемся находить значения синуса и косинуса по кругу

Давайте еще уточним следующее.

Ну хорошо, если нас просят вычислить, скажем, $\sin 30^{\circ}$ , – здесь обычно путаницы не возникает – все начинают первым делом искать $30^{\circ}$ на круге.

А если просят вычислить, например, $\sin0$ … Многие, вдруг, начинают не понимают где искать этот ноль… Частенько ищут его в начале координат. Почему?

1) Давайте договоримся раз и навсегда! То, что стоит после $\sin$ или $\cos$ – это аргумент=угол, а углы у нас располагаются на окружности, не ищите их на осяx! (Просто отдельные точки попадают и на окружность, и на ось…) А сами значения синусов и косинусов – ищем на осях!

2) И еще! Если мы от точки «старт» отправляемся против часовой стрелки (основное направление обхода тригонометрического круга), то мы откладываем положительные значения углов, значения углов растут при движении в этом направлении.

Если же мы от точки «старт» отправляемся по часовой стрелке, то мы откладываем отрицательные значения углов.

Пример 1. Найти значение $\sin 0^{\circ}$ .

Решение: + показать

Пример 2. Найти значение $\sin 270^{\circ}$ .

Решение: + показать

Заметим, + показать

например, за точкой $270^{\circ}$ «скрываются» такие точки, как $-90^{\circ}$ (мы могли бы пойти в точку, помеченную как $270^{\circ}$ , по часовой стрелке, а значит появляется знак минус), $270^{\circ}+360^{\circ}$ и бесконечно много других.

Можно привести такую аналогию:

Представим тригонометрический круг как беговую дорожку стадиона.

futb-pole

Вы ведь можете оказаться в точке «Флажок», отправляюсь со старта против часовой стрелки, пробежав, допустим, 300 м. Или пробежав, скажем, 100м по часовой стрелке (считаем длину дорожки 400 м).

А также вы можете оказаться в точке «Флажок» (после «старт»), пробежав, скажем, 700 м, 1100 м, 1500 м и т. д. против часовой стрелки. Вы можете оказаться в точке «Флажок», пробежав 500 м или 900 м и т. д. по часовой стрелке от «старт».

Разверните мысленно беговую дорожку стадиона в числовую прямую. Представьте, где на этой прямой будут, например, значения 300, 700, 1100, 1500 и т.д. Мы увидим точки на числовой прямой, равноотстоящие друг от друга. Свернем обратно в круг. Точки «cлепятся» в одну.

Так и с тригонометрическим кругом. За каждой точкой скрыто бесконечно много других.

Скажем, углы $30^{\circ}$ , $390^{\circ}$ , $750^{\circ}$ , $-330^{\circ}$ и т.д. изображаются одной точкой. И значения синуса, косинуса в них, конечно же, совпадают. (Вы заметили, что мы прибавляли/вычитали $360^{\circ}$ или $2\pi$ ? Это период для функции синус и косинус.)

Пример 3. Найти значение $\sin (-\frac{7\pi}{6})$ .

Решение: + показать

Пример 4. Найти значение $\cos \frac{5\pi}{4}$ .

Решение: + показать

Пример 5. Найти значение $\cos (-\frac{25\pi}{6})$ .

Решение: + показать

Пример 6. Найти значение $\cos (-1500^{\circ})$ .

Решение: + показать

Тригонометрический круг – у вас в руках

Вы же уже поняли, что главное – запомнить значения тригонометрических функций первой четверти. В остальных четвертях все аналогично, нужно лишь следить за знаками. А «цепочку-лесенку» значений тригонометрических функций, вы, надеюсь уже не забудете. тригонометрия в руке

Как находить значения тангенса и котангенса основных углов смотрите здесь

Unknown После чего, познакомившись с основными значениями тангенса и котангенса, вы можете пройти тест по теме «Нахождение значений косинусов, синусов, тангенсов и котангенсов различных углов»

Ссылочка на пустой шаблон круга. Тренируйтесь!

Автор: egeMax | комментария 2

Печать страницы

комментария 2

Сергей

2015-07-30 в 05:23

Здравствуйте, могли бы вы подсказать, что значит свойство sin (t+pi/2)=cos t и cos(t+pi/2)=-sin t ? А как это возможно, если мы на 90 градусов уйдем влево-вправо, поменяется четверть круга, и знак, соответственно, почему же у косинуса будет тот же знак, что и у синуса t+пи/2 ?

[ Ответить ]
- egeMax
  
  2015-07-30 в 08:20
  
  Сергей, вам сюда.
  
  [ Ответить ]

Тригонометрический круг II

Перевод радиан в градусы и градусы в радианы

Тренируемся находить значения синуса и косинуса по кругу

Тригонометрический круг – у вас в руках

Добавить комментарий Отменить ответ