Площадь ортогональной проекции многоугольника

Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекций.

Докажем теорему для треугольника. Поскольку многоугольник разбивается на треугольники, сумма площадей которых есть площадь многоугольника, то и для многоугольника теорема будет верна.

Доказательство:

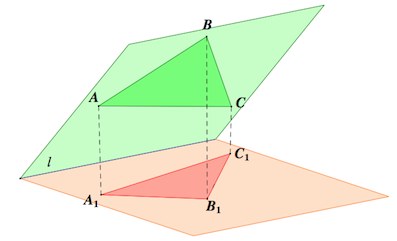
Пусть  треугольник $A_1B_1C_1$ – проекция  треугольника $ABC$ на проецируемую плоскость.

Докажем, что

$\color{red}S_{A_1B_1C_1}=S_{ABC}\cdot cos\alpha $,

где $\alpha$ – угол между плоскостями $ABC,\;A_1B_1C_1$

Для этого разобьем треугольник  $ABC$ на два треугольника c общей стороной $AM$, параллельной прямой $l$ пересечения плоскостей $ABC,\;A_1B_1C_1$. (Частный случай, когда одна из сторон треугольника $ABC$ параллельна линии пересечения плоскостей $l$, можно рассмотреть отдельно (самостоятельно)).

Проекция треугольника $ABM$ –   треугольник $A_1B_1M_1$. Причем $AM=A_1M_1$.

Пусть $BH$ – перпендикуляр к $l$. Тогда по т. о трех перпендикулярах и $B_1H$ – перпендикуляр к $l$.  Стало быть, $\angle BHB_1=\alpha$ – угол между плоскостями треугольников (проецируемого и проекции).

Пусть $T$ – точка пересечения $BH$ и $AM$, $T_1$ – проекция т. $T$ на плоскость $A_1B_1C_1$. Очевидно, $BT$ – высота треугольника $ABM$ ($B_1T_1$ – высота треугольника $A_1B_1M_1$).

Из треугольника $BHB_1$

$cos\alpha =\frac{B_1H}{BH}$

Но и

$\frac{HT_1}{HT}=cos\alpha $

Тогда $BT=BH-HT=\frac{1}{cos\alpha }(BH_1-HT_1)=\frac{B_1T_1}{cos\alpha}.$

Имеем: $S_{ABM}=\frac{1}{2}BT\cdot AM=\frac{1}{2}\cdot \frac{B_1T_1}{cos\alpha}\cdot AM=\frac{S_{A_1B_1M_1}}{{cos\alpha}}.$

Аналогичные рассуждения – для пары треугольников $AMC$ и $A_1M_1C_1$:

$S_{AMC}=\frac{1}{2}CR\cdot AM=\frac{1}{2}\cdot \frac{C_1R_1}{cos\alpha}\cdot AM=\frac{S_{A_1M_1C_1}}{{cos\alpha}}$

(где $CR$ – высота треугольника $ACM$, $C_1R_1$ – ее проекция)

Итак, суммируя площади треугольников $ABM,\;ACM$ и $A_1B_1M_1,\;A_1C_1M_1$ соответственно, получаем

$S_{ABC}=\frac{S_{A_1B_1C_1}}{cos\alpha}$

или

$S_{A_1B_1C_1}=S_{ABC}\cdot cos\alpha $

Что и требовалось доказать.

Пример. 

Ребро куба равно 2 см. Через диагональ основания под углом $45^{\circ}$ к плоскости основания проведена плоскость, пересекающая боковое ребро. Найти площадь сечения.

Решение:

Пусть плоскость сечения проведена через диагональ $BD$ и пересекает боковое ребро  ($CC_1$) в точке $T$.

По вышеуказанной теореме

$S_{BDT}=\frac{S_{BCD}}{cos\alpha},$

где треугольник $BCD$ – проекция треугольника $BTD$ на плоскость основания, $\alpha$ – угол между плоскостями $BCD,\;BTD.$

$S_{BDT}=\frac{2}{\frac{\sqrt2}{2}}=2\sqrt2.$

Ответ: $2\sqrt2.$

Применение теоремы можно также посмотреть, например, в этой задаче.