С2 (№16)

1) Построение сечения.

Так как по условию  ребро $AS$ должно быть параллельно сечению, то в плоскостях граней $ASD,\;ASB$ через точки $F$ и $E$ соответственно проводим прямые, параллельные ребру $AS$. Пусть указанные прямые пересекаются с ребрами $SD,\;SB$ в точках $L$ и $N$.  Далее в плоскости $ASC$ через точку $M$  ($M$ – точка пересечения $EF$ и $AC$) проводим прямую, параллельную $AS$.  Пусть она пересекает $SO,\;SC$ в точках $R,\;T$ соответственно.

Пятиугольник $ENTLF$ – искомое сечение.

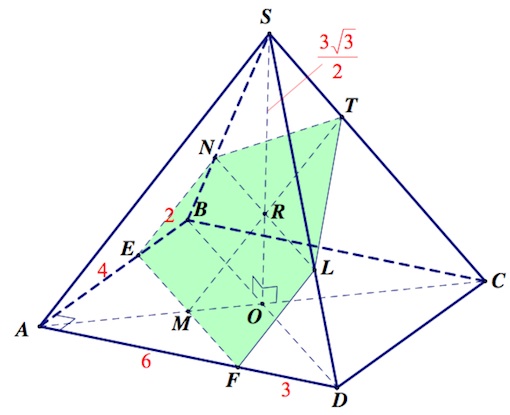
2) Будем искать площадь пятиугольника $ENTLF$ через площадь проекции его на плоскость основания пирамиды. А именно,

$\color{red}S_{ENTLF}=\frac{S_{proeksia}}{cos\alpha}$,

где $\alpha$ – угол между плоскостями $ABCD$ и $ENTLF,$

$S_{proeksia}$ – площадь проекции сечения $ENTLF$ на плоскость основания пирамиды.

Нам предстоит найти

– $S_{proeksia},$

– $cos\alpha.$

3) Поиск площади проекции сечения:

Проекция сечения  $ENTLF$ – пятиугольник $EN_1T_1L_1F.$ Причем $EN_1L_1F$ – параллелограмм, $FL_1\parallel MO,$ $OM=FL_1=OT_1,\;N_1O=L_1O$

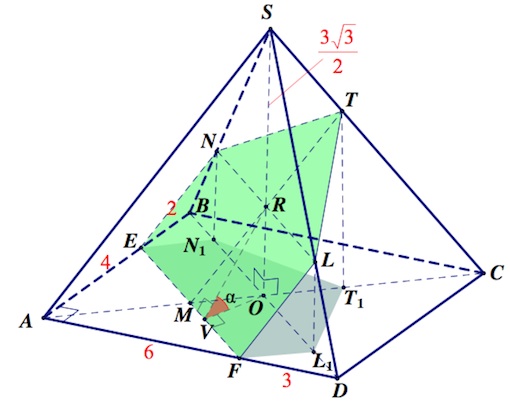
Прежде  нам предстоит найти всевозможные вспомогательные элементы.

а) Заметим, так как $AE:AB=AF:AD=3:2$ и $\angle A$ – общий для треугольников  $AEF$ и $ABD$, то имеем подобие треугольников $AEF,\;ABD$ по II признаку.

Откуда  $EF=\frac{2}{3}BD$   и   $EF\parallel BD.$ 

Далее из  треугольника $ABD$ по т. Пифагора:

$BD=\sqrt{6^2+9^2}=3\sqrt{13}.$

Заметим, диагонали в прямоугольнике равны, то есть $AC=BD=3\sqrt{13}.$

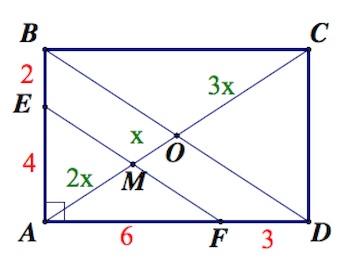
Тогда $EF=\frac{2}{3}\cdot 3\sqrt{13}=2\sqrt{13};$

Так как $AM:AO=2:3$, то $OM=\frac{1}{3}AO=\frac{\sqrt{13}}{2}.$

б) Треугольники  $ASC$ и $MTC$ подобны, коэффициент подобия $k=CM:CA=2:3.$ Тогда $MT=\frac{2}{3}AS.$

Найдем $AS$ из прямоугольного треугольника $ASO:$

$AS=\sqrt{(\frac{3\sqrt3}{2})^2+(\frac{3\sqrt{13}}{2})^2}=6.$

в) Заметим, $sin\angle L_1FE=sin \angle COD=sin\angle COB$ (нам они потребуются для вычисления площади проекции).

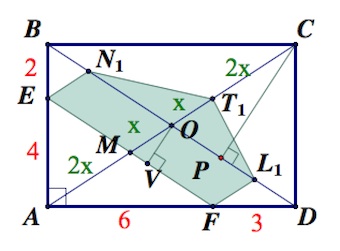
Из $\Delta OCP$ ($CP\perp OD$):

$sin\angle COP=\frac{CP}{OC}$

Найдем $CP$:

Из треугольника $COD:$

$\frac{1}{2}CP\cdot OD=\frac{1}{2}\cdot \frac{1}{2}AD\cdot CD$

(подсчет площади через разные высоты).

Тогда

$CP=\frac{4,5\cdot 6}{\frac{3\sqrt{13}}{2}}=\frac{18}{\sqrt{13}};$

Стало быть,

 $sin\angle COP=\frac{\frac{18}{\sqrt{13}}}{\frac{3\sqrt{13}}{2}}}=\frac{12}{13}.$

Площадь проекции:
$S_{EN_1T_1L_1F}=S_{EN_1L_1F}+S_{N_1T_1O}+S_{OT_1L_1}=$
$=(2\sqrt{13}\cdot \frac{\sqrt{13}}{2}\cdot \frac{12}{13})+2(\frac{1}{2}\sqrt{13}\cdot \frac{\sqrt{13}}{2}\cdot \frac{12}{13})=12+6=18.$

4) Поиск косинуса угла между плоскостями сечения и основания:

Пусть $OV$ – перпендикуляр к $EF$. Тогда по т. о трех перпендикулярах и $RV\perp EF$, то ест $\alpha=\angle RVO$ – угол между плоскостями $ABCD$ и $ENT.$

Найдем $cos\alpha $, для чего прежде вычислим длину $OV.$

$OV:CP=1:3$, где $CP$ – перпендикуляр к $BD$ (из подобия треугольников $COP,\;OVM$).

$OV=\frac{1}{3}CP=\frac{6}{\sqrt{13}}.$

$cos\alpha=\frac{OV}{RV}=\frac{OV}{\sqrt{OV^2+OR^2}}=\frac{\frac{6}{\sqrt{13}}}{\sqrt{(\frac{6}{\sqrt{13}})^2+(\frac{\sqrt3}{2})^2}}=$

$=\frac{\frac{6}{\sqrt{13}}}{\sqrt{\frac{144+39}{52}}}=\frac{6\sqrt{52}}{\sqrt{13}\cdot \sqrt{183}}=\frac{12}{\sqrt{183}}.$

Наконец, $S_{ENTLF}=\frac{S_{EN_1T_1L_1F}}{cos\alpha}=\frac{18}{\frac{12}{\sqrt{183}}}=\frac{3\sqrt{183}}{2}.$