Призма. Виды призмы

Если вы уже знакомы с призмой, и хотите для себя просто что-то уточнить, то вам вполне может хватить таблицы, что дана в конце статьи.

Мы же поведем  подробный разговор.

Призмой (n-угольной призмой) называется многогранник, составленный из двух равных многоугольников $A_1A_2…A_n$ и $B_1B_2…B_n$, лежащих в параллельных плоскостях, и $n$ параллелограммов $A_1A_2B_2B_1,…,\;A_1A_nB_nB_1$.

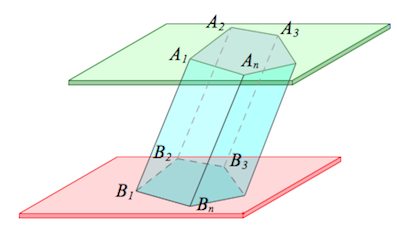
Указанные в определении равные многоугольники – основания призмы.

Боковые грани – все грани, кроме оснований (являются параллелограммами).

Боковые ребра – общие стороны боковых граней (параллельны между собой и равны).

Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

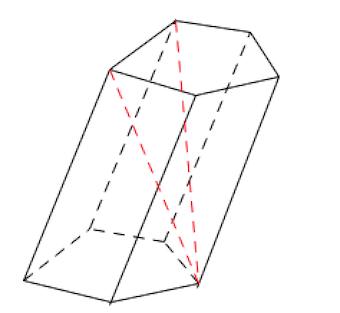
Высота призмы – перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания.

Диагональное сечение –пересечение призмы и диагональной плоскости.

Перпендикулярное сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

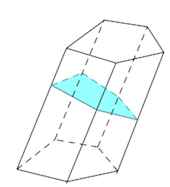
Различают призмы прямые (боковые ребра перпендикулярны плоскости основания) и наклонные (не прямые).

Среди прямых призм выделяют правильные.

Правильная  призма – это прямая призма, основанием которой является правильный многоугольник (равносторонний треугольник, квадрат, правильный шестиугольник и т.п.).

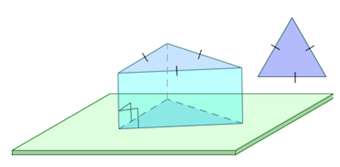
Частным случаем призмы является параллелепипед.

Параллелепипед – это призма, основаниями которой являются параллелограммы.

Среди параллелепипедов выделяют наклонные, прямые и прямоугольные параллелепипеды.

Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники.

Прямоугольный параллелепипед  — это параллелепипед, у которого все грани — прямоугольники (или прямой параллелепипед с прямоугольником в основании).

Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.

Частный случай прямоугольного параллелепипеда – куб.

Куб – прямоугольный параллелепипед, все грани которого – квадраты.

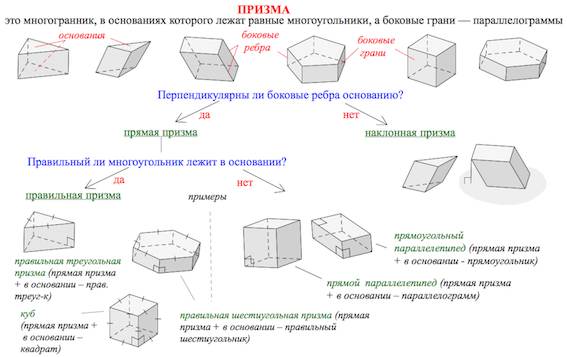
Далее – обещанная таблица, в которой собраны все основные виды призмы, с которыми приходится встречаться на ЕГЭ по математике.

Нажмите сюда чтобы увеличить

  Смотрите также «Объем призмы. Площадь поверхности призмы».