Определение. Геометрический смысл
Модуль (или абсолютная величина)числа $x$ (обозначается как $|x|$)— неотрицательное число, определение которого зависит от типа числа $x.$
А именно:
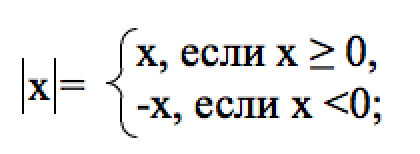
Мы будем называть данное правило правилом раскрытия модуля.
Например, $|5|=5,$ так как $5\geq0$, попадаем в первую строку (ситуацию).
$|-4|=-(-4)=4,$ так как $-4<0,$ попадаем во вторую ситуацию.
С геометрической точки зрения, $|x|$ – есть расстояние между числом $x$ и началом координат.
Решением уравнения, например, $|x|=6$ являются числа $6$ и $-6$, потому что расстояние от точки $6$ координатной прямой до нуля равно $6$, и расстояние от точки $-6$ до нуля также равно 6.
|$a-b$| с геометрической точки зрения означает расстояние между точками $a$ и $b$.
Полезные примеры
1) Раскрыть модуль: $|\pi-3|$
Так как $\pi=3,1415926…$ больше, чем $3$, то $\pi-3>0$, а значит $|\pi-3|=\pi-3$ согласно правилу раскрытия модуля.
2) Раскрыть модуль: $|x^4+1|$
Так как $x^4+1$ больше нуля при всех значениях $x$, то $|x^4+1|=x^4+1$ согласно правилу раскрытия модуля.
3) Раскрыть модуль: $|2-\sqrt5|$
Так как $\sqrt5>\sqrt4=2$, то $2-\sqrt5<0$, а значит, $|2-\sqrt5|=\sqrt5-2$ согласно правилу раскрытия модуля.
Решение уравнений
1) Решить уравнение $|x^2-4x+3|=-2$ + показать
Модуль – всегда неотрицательная величина, поэтому уравнение решений не имеет.
Ответ: { $\varnothing$ }
2) Решить уравнение: $|x|=x$ + показать
Модуль раскрывается таким образом в случае, когда $x\geq 0$.
Ответ: $[0;+\infty).$
3) Решить уравнение: $|x-2|=|2-x|$ + показать
Согласно геометрическому смыслу модуля $|a-b|$ левая и правая части равенства представляют из себя одно и то же.
Ответ: $(-\infty;+\infty).$
4) Решить уравнение: $x|x|+8x-7=0$ + показать
Раскрываем модуль согласно правилу раскрытия модуля:
а) $\color{red}x\geq 0$
Имеем:
$x\cdot x+8x-7=0,$
$x^2+8x-7=0.$
Откуда $x=-4\pm \sqrt{23}$.
Поскольку мы находимся в ситуации $x\geq 0$, то подходит только корень $x=-4+\sqrt{23}$.
б) $\color{red}x<0$
Имеем:
$x\cdot(-x)+8x-7=0,$
$-x^2+8x-7=0.$
Откуда $x=7$ или $x=1$.
Поскольку мы находимся в ситуации $x<0$, то ни один корень из найденных в пункте (б) нам не подходит.
Ответ: $-4+\sqrt{23}$.
Коротко можно было бы решение оформить так:
5) Решить уравнение: $x^2-2|x-1|=2$ + показать
Раскрываем модуль согласно правилу раскрытия модуля:
a) Первый случай:
$\begin{cases}
x-1\geq 0,
\\x^2-2(x-1)=2;
\end{cases}$
$\begin{cases}
x\geq 1,
\\x^2-2x=0;
\end{cases}$
$\begin{cases}
x\geq 1,
\\x=0,\;x=2;
\end{cases}$
Что равносильно $x=2$.
б) Второй случай:
$\begin{cases}
x-1<0,
\\x^2-2(1-x)=2;
\end{cases}$
$\begin{cases}
x<1,
\\x^2+2x-4=0;
\end{cases}$
$\begin{cases}
x<1,
\\x=-1\pm\sqrt5;
\end{cases}$
Что равносильно $x=-1-\sqrt5$
Ответ: $2;\;-1-\sqrt5$
6) Решить уравнение: $|x^2+5x+6|=2$ + показать
Можно было бы действовать согласно правилу раскрытия модуля, но проще будет в данном случае рассуждать так:
Внутри модуля $|…|$ может «скрываться» как $2,$ так и $-2$.
Поэтому $x^2+5x+6=2$ или $x^2+5x+6=-2$
$x^2+5x+4=0$ или $x^2+5x+8=0$
Из первого уравнения $x=-4$ или $x=-1$, а второе уравнение корней не имеет.
Ответ: $-4;\;-1.$
7) Решить уравнение: $|x^3-x|=x+4$ + показать
Раскрываем модуль согласно правилу раскрытия модуля:
а) Первый случай:
$\begin{cases}
x^3-x\geq 0,
\\x^3-x=x+4;&
\end{cases}$
Рассмотрим отдельно первую строку системы:
$x^3-x\geq 0$
$x(x^2-1)\geq 0$
$x(x-1)(x+1)\geq 0$
Рассмотрим уравнение из системы:
$x^3-x=x+4$ или $x^3-2x-4=0$
Разложим на множители левую часть уравнения способом группировки, предварительно разбив среднее слагаемое на два:
$x^3-4x+2x-4=0$
$x(x^2-4)+2(x-2)=0$
$x(x-2)(x+2)+2(x-2)=0$
$(x-2)(x(x+2)+2)=0$
$(x-2)(x^2+2x+4)=0$
Откуда $x=2$ (трехчлен в скобках корней не имеет).
Данный корень удовлетворяет первой строке системы, он пойдет в ответ.
б) Второй случай:
$\begin{cases}
x^3-x< 0,
\\-x^3+x=x+4;&
\end{cases}$
$\begin{cases}
x^3-x< 0,
\\x=-\sqrt[3]4;&
\end{cases}$
Решение неравенства системы:
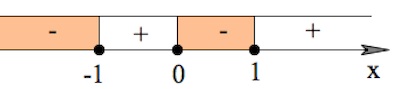
Корень $x=-\sqrt[3]4$ удовлетворяет решению неравенства системы.
Собираем решения.
Ответ: $2;\;-\sqrt[3]4.$
Также, смотрите «Модуль. Простейшие неравенства с модулем» здесь
Вы можете пройти тест по теме «Модуль. Раскрытие модуля. Простешие уравнения с модулем»
Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
Модуль (или абсолютная величина)числа $x$ (обозначается как $|x|$)— неотрицательное число, определение которого зависит от типа числа $x.$
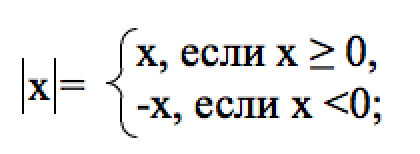
Рассмотрим уравнение из системы:
Почему в уравнении 4 б сохраняется знак + перед 8x, ведь x отрицательный?
Мы раскрываем МОДУЛЬ!!!
Понял, дурак)
;)