Главная › Справочные материалы › Треугольник

29 Июл 2013

Категория: Справочные материалы

Треугольник

Елена Репина 2013-07-29 2014-01-07

Треугольник произвольный

Треугольник – это многоугольник с тремя сторонами (тремя углами).

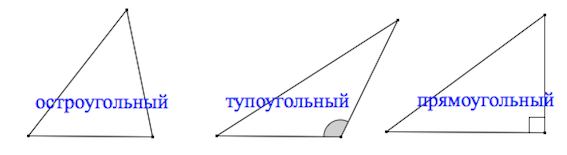
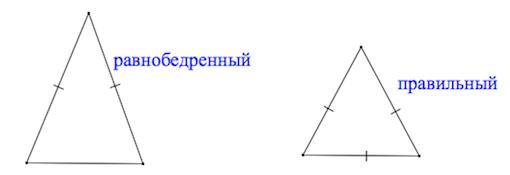
Виды треугольников:+ показать

Свойства

+ показать

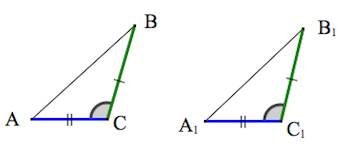
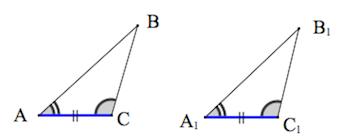
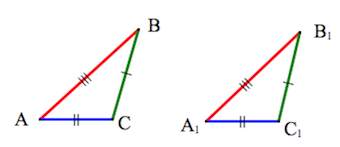
Признаки равенства треугольников

+ показать

Биссектриса, высота, медиана

Здесь подробно о биссектрисе, высоте, медиане треугольника.

Средняя линия треугольника

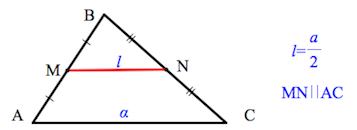
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.

Средняя линия треугольника параллельна третьей стороне и равна ее половине.

Вписанная окружность

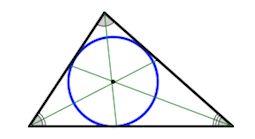
Центр вписанной окружности – точка пересечения биссектрис треугольника.

$r=\frac{S}{p}$

Снимок экрана 2013-07-29 в 19.07.59

Описанная окружность

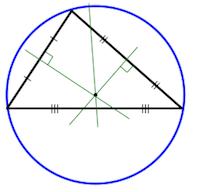
Центр описанной окружности – точка пересечения серединных перпендикуляров.

$R=\frac{abc}{4S}$

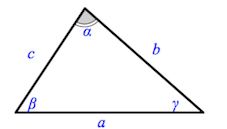
Соотношение сторон в произвольном треугольнике

Теорема косинусов: $a^2=b^2+c^2-2bcCos\alpha$

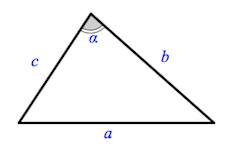
Теорема синусов: $\frac{a}{Sin\alpha}=\frac{b}{Sin\beta}=\frac{c}{Sin\gamma}=2R$

Площадь треугольника

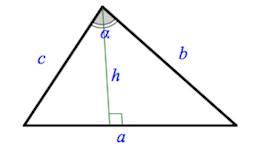Через сторону и высоту

$S=\frac{1}{2}ah_a$

Через две стороны и угол между ними

$S=\frac{1}{2}bcSin\alpha$

Через радиус описанной окружности

$S=\frac{abc}{4R}$

Через радиус вписанной окружности

$S=pr$ , где $p$ – полупериметр

Формула Герона

$S=\sqrt{p(p-a)(p-b)(p-c)}$ , где $p$ – полупериметр

внимание

Смотрите также площадь треугольника здесь.

И, думаю, будет полезна таблица формул для треугольника.

Автор: egeMax | комментариев 12 | Метки: шпаргалки-таблицы

Печать страницы

комментариев 12

Анатолий Шевелев

2013-12-26 в 20:39

Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”.
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен ;)

[ Ответить ]
- egeMax
  
  2013-12-26 в 21:01
  
  Анатолий, спасибо!
  В разделе “свойства” ошибок не нашла…
  В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
  В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
  К сожалению, ошибки сразу не всегда замечаются.
  Благодарю еще раз!
  
  [ Ответить ]
Анатолий Шевелев

2013-12-29 в 10:54

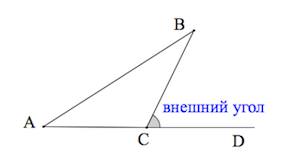
В разделе свойства: $\angle BCD=\abgle A+\angle B$

[ Ответить ]
- egeMax
  
  2013-12-29 в 11:44
  
  Да, не хватало значка « $\angle$ » у А. Спасибо! ;)
  
  [ Ответить ]
Ильяс

2015-03-31 в 16:13

Здраствуйте! Мне нужна ваша помощь!
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.

[ Ответить ]
- egeMax
  
  2015-03-31 в 16:20
  
  Подозреваю, у вас опечатка в условии…
  Если длины дуг (а значит и их градусные меры) находятся в отношении $6:7:23$ , то выходим на уравнение $6x+7x+23x=360^{\circ}.$ Откуда $x=10^{\circ}.$ Значит угол треугольника, что напротив меньшей стороны, есть $\frac{6x}{2}=30^{\circ}.$
  Применяем теорему синусов: $2R=\frac{11}{sin30^{\circ}}$ , откуда $R=11.$
  
  [ Ответить ]
Ильяс

2015-03-31 в 20:29

спасибо я так и думал а то не могу решить и всё
СПАСИБО!

[ Ответить ]
Анна

2015-10-25 в 13:11

Здравствуйте. Пожалуйста, объясните, как решить задачу:
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3

[ Ответить ]
- egeMax
  
  2015-10-25 в 19:46
  
  Очевидно, $AK=AM=2,MC=LC=3.$
  Примите $KB,BL$ за $x$ .
  Примените к треугольнику $ABC$ теорему косинусов:
  $(x+2)^2=5^2+(3+x)^2-2\cdot 5\cdot (3+x)\cdot \frac{1}{2}.$
  Найдете $x$ , далее можно найти угол $B$ и из треугольника $BKL$ найти $KL.$
  
  [ Ответить ]
Виктория

2015-11-08 в 20:39

Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно

[ Ответить ]
- egeMax
  
  2015-11-08 в 20:45
  
  Виктория, спасибо!
  
  [ Ответить ]
алиса

2015-12-01 в 22:27

Доказать равенство треугольников АВС и А1В1С1
Дано: сторона АВ равна А1В1, угол ВАС= углу В1А1С1
ВС+АС=В1С1+А1С1

[ Ответить ]