Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
Если вы уже знакомы с призмой, и хотите для себя просто что-то уточнить, то вам вполне может хватить таблицы, что дана в конце статьи.
Мы же поведем подробный разговор.
Архив по меткам: шпаргалки-таблицы
13
Авг 2013
Призма. Виды призмы
Елена Репина 2013-08-13 2023-08-03
29
Июл 2013
Треугольник
Елена Репина 2013-07-29 2023-08-06Треугольник произвольный
Треугольник – это многоугольник с тремя сторонами (тремя углами). Читать далее
30
Июн 2013
Формулы для решения простейших тригонометрических уравнений. Часть 1
Елена Репина 2013-06-30 2023-08-08Прежде чем решать тригонометрические уравнения, вы должны хорошо разбираться в тригонометрическом круге
Все тригонометрические уравнения, какими они не были – простыми или сложными, в итоге сводятся к решению четырех типов простейших тригонометрических уравнений.
Вы просто обязаны уметь решать уравнения вида Читать далее
15
Июн 2013
Метод рационализации. Часть 1
Елена Репина 2013-06-15 2023-08-08Подробнее (конкретные примеры, суть метода замены множителей) смотрим здесь. Читать далее
23
Май 2013
Вписанные, центральные углы
Елена Репина 2013-05-23 2023-08-10
22
Май 2013
Синус, косинус, тангенс в прямоугольном треугольнике
Елена Репина 2013-05-22 2023-08-10 
Гипотенузой называется та сторона треугольника, что лежит против угла в 90 градусов, две оставшиеся стороны называются катетами прямоугольного треугольника.
Подробнее про прямоугольный треугольник здесь
08
Май 2013
Пирамида, призма. Формулы объема и площади поверхности
Елена Репина 2013-05-08 2023-08-10
07
Май 2013
Тела вращения. Формулы объема и площади поверхности
Елена Репина 2013-05-07 2023-08-10
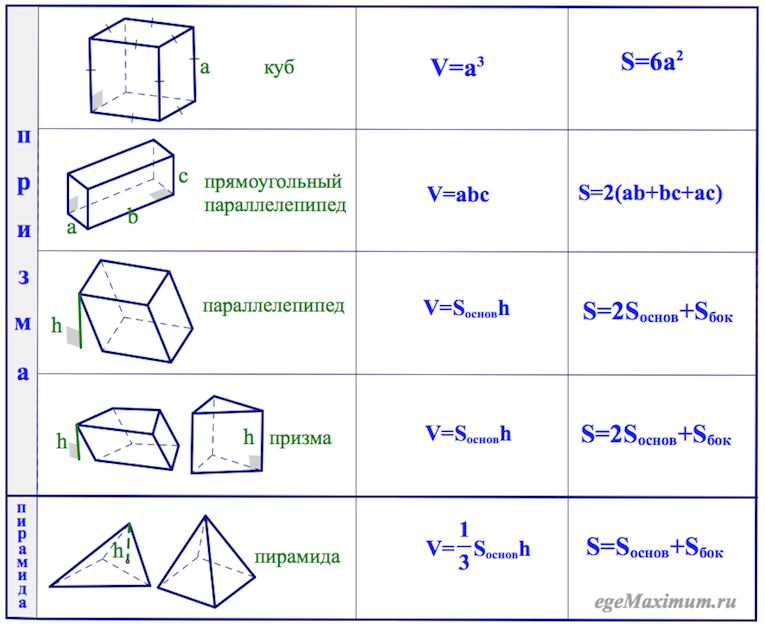
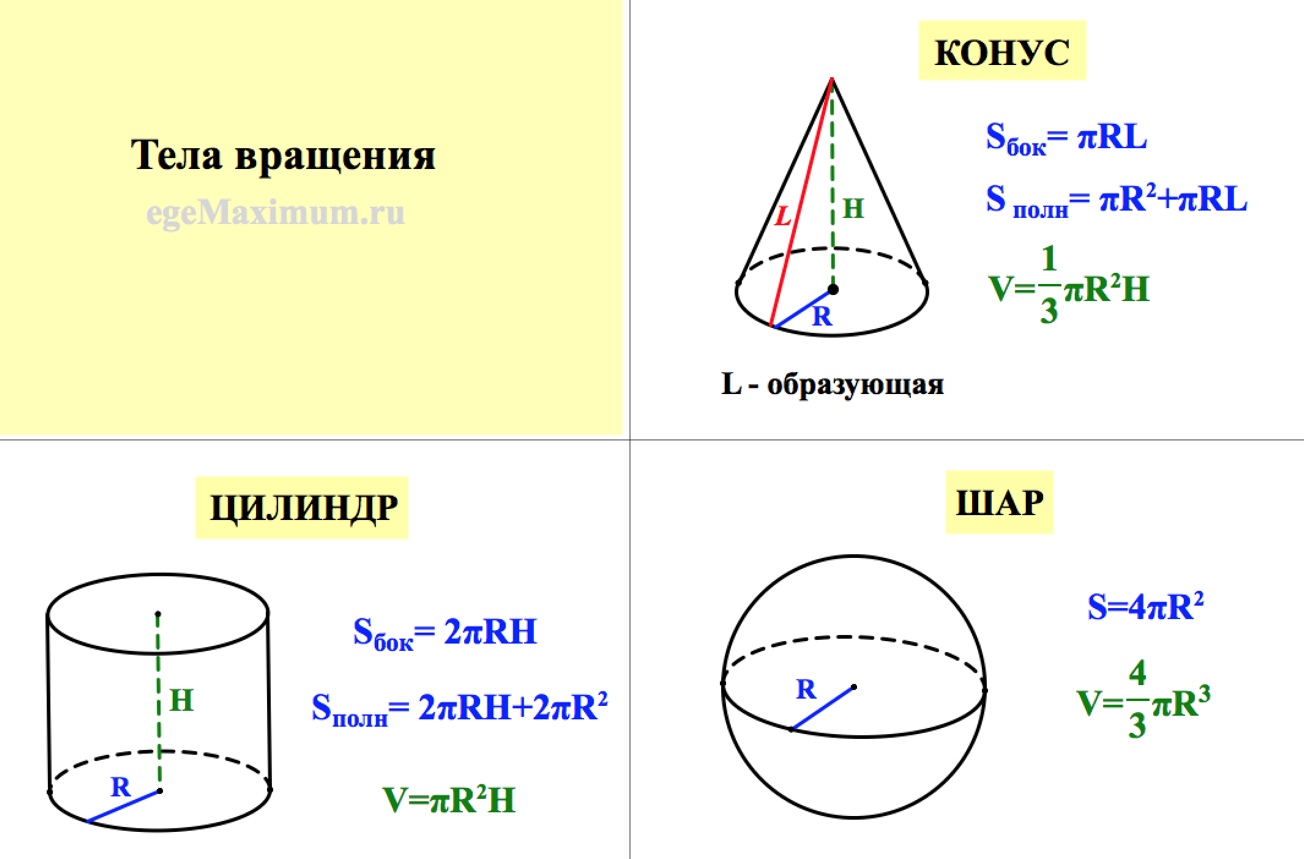
В частности,
18
Апр 2013
Квадратное уравнение
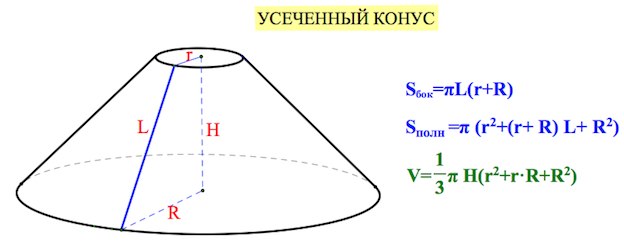
Елена Репина 2013-04-18 2023-08-11Загляни сюда, – вдруг узнаешь себя!
Надеюсь, вы внимательно изучили таблицу, приведенную выше. Если все еще есть вопросы, – давайте разбираться. Читать далее
16
Апр 2013
Таблица производных. Правила дифференцирования
Елена Репина 2013-04-16 2016-08-25
22
Фев 2013
Разложение на множители
Елена Репина 2013-02-22 2023-07-06Основные способы разложения многочлена на множители
1. Вынесение общего множителя за скобку
$\quad{\bigtriangleup \cdot \bigcirc +\bigtriangleup \cdot \bigstar =\bigtriangleup (\bigcirc +\bigstar )}$
20
Фев 2013
Тригонометрические формулы
Елена Репина 2013-02-20 2023-08-11Основные тригонометрические формулы
$\sin^2\alpha + cos^2 \alpha= 1$ Видео*
$tg\alpha =\frac{\sin\alpha }{\cos \alpha},\;ctg\alpha =\frac{\cos\alpha}{\sin\alpha}$
$tg^2\alpha + 1 = \frac{1}{\cos^2\alpha},\;ctg^2 \alpha + 1 = \frac{1}{\sin^2\alpha}$
20
Фев 2013
Степень числа. Корень
Елена Репина 2013-02-20 2023-08-11Натуральная степень числа
Число c называется n-й степенью числа a ( обозначается как $\color{ red} a^{n}$), если
$\color{red} c=\underbrace {a\cdot a\cdot…\cdot a}_{n\;{times}}$
18
Фев 2013
Логарифм. Определение. Свойства логарифмов
Елена Репина 2013-02-18 2023-07-06Логарифм числа $b$ по основанию $a$ определяется как показатель степени, в которую нужно возвести основание $a$, чтобы получить число $b$.
Обозначение $log_a b$ читается как логарифм $b$ по основанию $a$.
Например, $log_28=3$, так как $2^3=8$ ($2$ – основание степени, $3$ – показатель степени)
ЛОГАРИФМЫ
$\Large{\log_{a}b=c\Leftrightarrow a^{c}=b\;}\;$
17
Фев 2013
