Формулы для решения простейших тригонометрических уравнений. Часть 1

Мы должны подобрать такие значения аргумента $x$, то есть такие значения углов, косинус которых равнялся бы $\frac{1}{2}$.

Смотрим на тригонометрический круг, на оси косинусов находим $\frac{1}{2}$:

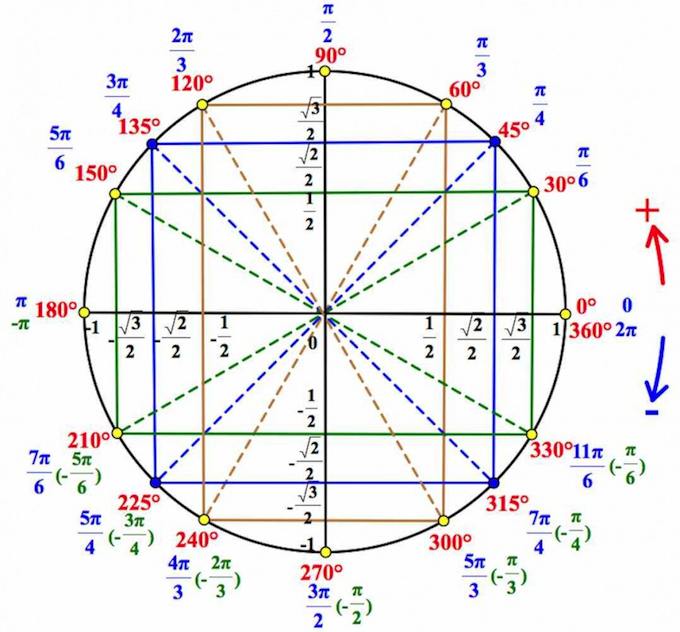
Выстраиваем через эту точку вертикаль, получаем две точки на круге:

Но надо понимать, что за этими точками скрывается бесконечно много других точек, – таких, косинус в которых также равен $\frac{1}{2}$. Мы об этом подробно говорили в предыдущей статье, когда знакомились с тригонометрическим кругом.

На координатной прямой подходящие нам точки располагаются  так:

А с графической точки зрения решение уравнения  $cos\:x=\frac{1}{2}$ выглядело бы так:

Как все точки взять в ответ?

Нам поможет счетчик $n$. Возьмем $n\in Z$, то есть $n=…-3,\;-2,\;-1,\;0,\;1,\;2,\;3,\;…$

Решением уравнения $cos\:x=\frac{1}{2}$ будет

$x=\pm\frac{\pi}{3}+2\pi n,\;n\in Z$

Возьмите, поперебирайте различные значения $n,$ подставьте в вышеуказанную формулу.

Вы получите как раз точки $\pm\frac{\pi}{3}$  при $n=0$,

$\frac{7\pi}{3},\;\frac{5\pi}{3}$ при $n=1$,

$\frac{13\pi}{3},\;\frac{11\pi}{3}$ при $n=2$ и т.д.

То что нам нужно!

Если бы мы решали, например,  уравнение $cos\:x=-\frac{\sqrt2}{2}$, то решением бы было

$x=\pm\frac{3\pi}{4}+2\pi n,\;n\in Z$

Если нам попадается уравнение с нетабличным значением косинуса, вроде этого $cos\:x=0,3$, то решение будет следующее:

 $x=\pm arccos\:0,3+2\pi n,\;n\in Z.$

1) $cos\:x=0$

 Мы должны бы записать так:

$x=\pm\frac{\pi}{2}+2\pi n,n\in Z$.

Но можно записать решение иначе (ведь в данном случае между точками расстояние – полкруга, значит нам можно использовать полукруговой счетчик $\pi n$):

$x=\frac{\pi}{2}+\pi n,\;n\in Z.$

2) $cos\:x=1$

У нас только одна серия корней:

$x=0+2\pi n,n\in Z,$ то есть $x=2\pi n,n\in Z.$

3) $cos\:x=-1$

Аналогично решению примера 2, решение такое: $x=\pi+2\pi n,\;n\in Z.$