Главная › 12 (С1) Уравнения › Задание №15 Т/Р №100 А. Ларина

22 Янв 2015

Категория: 12 (С1) УравненияТ/P A. ЛаринаТригонометрические выражения, уравнения и неравенства

Задание №15 Т/Р №100 А. Ларина

Елена Репина 2015-01-22 2015-09-04

Ранее задание значилось под №15. Сейчас – под №13 (С1).

Смотрите также №16, №17, №18, №20.

Дано уравнение:

$log_{100}(cos2x+cos\frac{x}{2})+log_{\frac{1}{100}}(sinx+cos\frac{x}{2})=0.$

a) Решите уравнение;

б) Найдите его корни, принадлежащие отрезку $[\frac{\pi}{2};2\pi].$

Решение:

а)

$log_{100}(cos2x+cos\frac{x}{2})=log_{100}(sinx+cos\frac{x}{2});$

$\begin{cases} cos2x+cos\frac{x}{2}=sinx+cos\frac{x}{2},& &sinx+cos\frac{x}{2}>0;& \end{cases}$

$\begin{cases} 1-2sin^2x=sinx,& &sinx+cos\frac{x}{2}>0;& \end{cases}$

$\begin{cases} 2sin^2x+sinx-1=0,& &sinx+cos\frac{x}{2}>0;& \end{cases}$

$\begin{cases} \left[\begin{gathered} sinx=-1,& sinx=\frac{1}{2}; \end{gathered}\right& &sinx+cos\frac{x}{2}>0;& \end{cases}$

$\begin{cases} \left[\begin{gathered} x=-\frac{\pi}{2}+2\pi n,n\in Z,& x=\frac{\pi}{6}+2\pi k, k\in Z,& x=\frac{5\pi}{6}+2\pi k, k\in Z;& \end{gathered}\right& &sinx+cos\frac{x}{2}>0;& \end{cases}$

Очевидно, решение первой строки совокупности не удовлетворяет неравенству $sinx+cos\frac{x}{2}>0.$

Проверим, удовлетворяют ли решения 2-й и 3-й строк совокупности неравенству $sinx+cos\frac{x}{2}>0:$

При $x=\frac{\pi}{6}+2\pi k, k\in Z$ значение выражения $sinx+cos\frac{x}{2}$ может быть как отрицательным, так и положительным.

А именно (заметив, что $\frac{\pi}{12}+\pi k, k\in Z$ – это объединение $\frac{\pi}{12}+2\pi m, m\in Z$ и $\frac{13\pi}{12}+2\pi m, m\in Z$ ),

$\frac{1}{2}+cos(\frac{\pi}{12}+2\pi m)>0, m\in Z,$ так как $cos\frac{\pi}{12}>0;$

$\frac{1}{2}+cos(\frac{13\pi}{12}+2\pi m)<0, m\in Z,$ так как $cos\frac{13\pi}{12}<-\frac{1}{2};$

kjlk

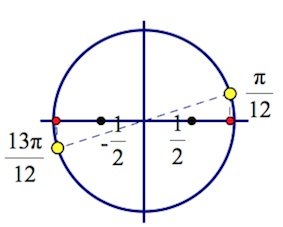
То есть отбираем следующие корни: $x=\frac{\pi}{6}+4\pi m, m\in Z$ .

При $x=\frac{5\pi}{6}+2\pi k, k\in Z$ значение выражения $sinx+cos\frac{x}{2}$ положительно.

Действительно (заметим, что $\frac{5\pi}{12}+\pi k, k\in Z$ – это объединение $\frac{5\pi}{12}+2\pi l, l\in Z$ и $\frac{17\pi}{12}+2\pi l, l\in Z$ ),

$\frac{1}{2}+cos(\frac{5\pi}{12}+2\pi l)>0, l\in Z,$ так как $cos\frac{5\pi}{12}>0;$

$\frac{1}{2}+cos(\frac{17\pi}{12}+2\pi l)<0, l\in Z,$ так как $cos\frac{17\pi}{12}>-\frac{1}{2};$

hjk,

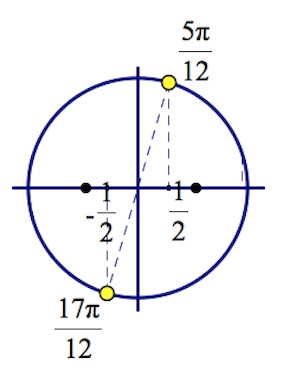
Итак, решение данного уравнения – $x=\frac{5\pi}{6}+2\pi k$ и $x=\frac{\pi}{6}+4\pi m, m\in Z$ .

б) Произведем отбор корней уравнения из отрезка $[\frac{\pi}{2};2\pi].$

kjijhm

Ответ:

а) $\frac{5\pi}{6}+2\pi k$ , $\frac{\pi}{6}+4\pi m, k, m\in Z$ .

б) $\frac{5\pi}{6}.$

Автор: egeMax | комментария 3

Печать страницы

комментария 3

Дима

2015-03-19 в 16:55

Почему не нужно писать, что cos(2x)+cos(x/2)>0??

[ Ответить ]
- egeMax
  
  2015-03-19 в 17:14
  
  Дмитрий, потому что $cos2x+cos\frac{x}{2}=sinx+cos\frac{x}{2}$ , а про сумму $sinx+cos\frac{x}{2}$ мы сказали, что она больше нуля, значит, автоматически, сказали и про $cos2x+cos\frac{x}{2}$ .
  
  [ Ответить ]
  - Дима
    
    2015-03-25 в 15:55
    
    Примерно понятно, большое спасибо
    
    [ Ответить ]

Задание №15 Т/Р №100 А. Ларина

Добавить комментарий Отменить ответ