Задание №18 Т/Р №100 А. Ларина

Смотрите также  №15, №16, №17, №20

В выпуклом четырехугольнике $ABCD$ диагонали $AC$ и $BD$ взаимно перпендикулярны. Кроме того, вокруг него можно описать окружность. Из точек $B$ и $C$ опущены перпендикуляры на прямую $AD$. Они пересекают прямые $AC$ и $BD$ соответственно в точках $E$ и $F$.

а) Докажите, что $BCEF$ – ромб
б) Найдите отношение площади четырехугольника $BCEF$ к площади вписанного в него круга, если $BF:CE=3:4.$

Решение:

а) Углы $1$ и $2$ (см. рис.), как вписанные углы, опирающиеся на одну дугу, равны.

Углы $3$ и $4$ равны как углы, дополняющие равные углы $1$ и $2$ до $90^{\circ}$ (в треугольниках $BCT$ и $FDH_2$ соответственно).

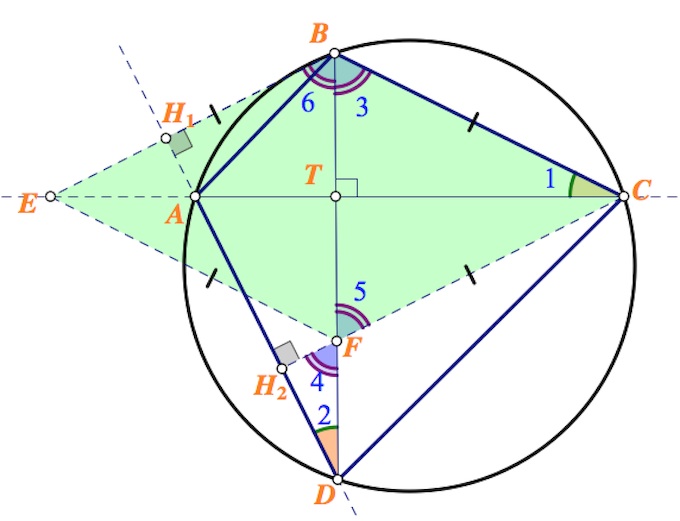
Из равных треугольников $BCT$ и $FCT$ ($T$ – точка пересечения диагоналей $ABCD$) (по катету и острому углу– $TC=TC,$  $\angle 3=\angle 5$) следует: $BC=CF$ и $BT=FT.$

Углы $6$ и $3$ равны как углы, дополняющие равные углы $1$ и $2$ до $90^{\circ}$ (в треугольниках $BDH_1$ и $BCT$ соответственно).

Из равных треугольников $EBT$ и $CBT$ (по катету и острому углу – $BT=BT$,  $\angle 3=\angle 6$) следует: $BE=BC.$

Из равных треугольников $EBT$ и $EFT$ (по двум катетам  – $ET=ET,$  $BT=FT$) следует: $BE=EF.$

Итак, в четырехугольнике $BCEF$    $BC=CF=EF=EB$, то есть $BCEF$ – ромб.

б) Распишем площадь треугольника $ETF$ двумя способами:

$\frac{1}{2}\cdot ET\cdot TF=\frac{1}{2}\cdot HT\cdot EF,$

где $TH\perp EF.$

Так как по условию $BF:CE=3:4$, то пусть $ET=2x,TF=1,5x.$

Тогда $HT=\frac{2x\cdot 1,5x}{\sqrt{(2x)^2+(1,5x)^2}}=\frac{3x^2}{\frac{5}{2}x}=\frac{6}{5}x.$

 $HT$ – и есть радиус вписанного в ромб круга.

Итак,

$\frac{S_{BCFE}}{S_{krug}}=\frac{\frac{1}{2}BF\cdot CE}{\pi HT^2}=\frac{\frac{1}{2}\cdot 3x\cdot 4x}{\pi \cdot \frac{36}{25}x^2}=\frac{6}{\frac{36}{25}\pi}=\frac{25}{6\pi}.$

Ответ: $\frac{25}{6\pi}.$