Главная › 14 (С3) Неравенства › Задание №17 Т/Р №103 А. Ларина

05 Фев 2015

Категория: 14 (С3) НеравенстваЛогарифмыМетод рационализацииТ/P A. Ларина

Задание №17 Т/Р №103 А. Ларина

Елена Репина 2015-02-05 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №15»

Смотрите также №15, №16, №18, №19, №20.

Решите неравенство

$\frac{\sqrt{6+x-x^2}}{log_2(5-2x)}\leq \frac{\sqrt{6+x-x^2}}{log_2(x+4)}.$

Решение:

$\sqrt{6+x-x^2}(\frac{1}{log_2(5-2x)}-\frac{1}{log_2(x+4)})\leq 0;$

$\sqrt{6+x-x^2}(\frac{log_2(x+4)-log_2(5-2x)}{log_2(5-2x)\cdot log_2(x+4)})\leq 0;$

Случай 1.

$x=-2$ или $x=3$ (нули квадратного трехчлена $6+x-x^2$ ).

Заметим, $x=-2$ являются решениями исходного неравенства, а $x=3$ – нет.

Случай 2.

$x\neq -2, x\neq 3.$

Мы можем обе части неравенства поделить на $\sqrt{6+x-x^2}$ (с соблюдением условия $6+x-x^2>0$ ):

$\begin{cases} \frac{log_2(x+4)-log_2(5-2x)}{log_2(5-2x)\cdot log_2(x+4)}\leq 0,& &6+x-x^2>0; \end{cases}$

К первой строке неравенства применяем метод замены множителей (метод рационализации):

$\begin{cases} \frac{(x+4)-(5-2x)}{(5-2x-1)(x+4-1)}\leq 0,& &x+4>0,& &5-2x>0,& &x^2-x-6<0; \end{cases}$

$\begin{cases} \frac{3x-1}{(4-2x)(x+3)}\leq 0,& &x>-4,& &x<2,5,& &(x+2)(x-3)<0; \end{cases}$

kmn

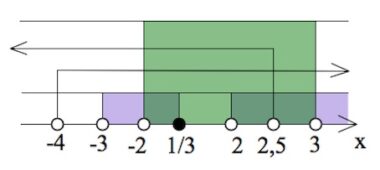
Итак, во втором случае имеем:

$x\in (-2;\frac{1}{3}]\cup (2;2,5).$

Наконец, объединяя решения случаев 1 и 2, получаем:

$x\in [-2;\frac{1}{3}]\cup (2;2,5).$

Ответ: $[-2;\frac{1}{3}]\cup (2;2,5).$

Автор: egeMax | Нет комментариев

Печать страницы

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (12)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (79)
- 13 (С2) Стереометр. задачи (95)
- 14 (С3) Неравенства (90)
- 15 (С4) Практич. задачи (72)
- 16 (С5) Планиметр. задачи (87)
- 17 (С6) Параметры* (80)
- 18 (С7) Числа, их свойства (39)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Задачи (28)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (59)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы