Задание №17 Т/Р №102 А. Ларина

Елена Репина 2015-01-29 2016-08-27

В новом формате ЕГЭ по математике задание значится как «Задание №15»

Решите неравенство:

$log_3(x^2-4x+5)\leq \frac{2x}{log_{x^2-4x+5}(9^x+3^x-12)}.$

Решение:

$log_3(x^2-4x+5)\leq \frac{2x}{log_{x^2-4x+5}(9^x+3^312)};$

$\frac{log_3(x^2-4x+5)\cdot log_{x^2-4x+5}(9^x+3^x-12)-2x}{log_{x^2-4x+5}(9^x+3^x-12)}\leq 0;$

$\frac{log_3(9^x+3^x-12)-2x}{log_{x^2-4x+5}(9^x+3^x-12)}\leq 0;$

Применяем метод замены множителей:

$\begin{cases} \frac{9^x+3^x-12-3^{2x}}{(x^2-4x+5-1)(9^x+3^x-12-1)}\leq 0,& &9^x+3^x-12>0,& &x^2-4x+5>0,& &x^2-4x+5\neq 1;& \end{cases}$

$\begin{cases} \frac{3^x-12}{(x^2-4x+4)(9^x+3^x-13)}\leq 0,& &(3^x-3)(3^x+4)>0,& &(x-2)^2\neq 0;& \end{cases}$

$\begin{cases} \frac{3^x-12}{(x-2)^2(3^x-\frac{-1+\sqrt{53}}{2})(3^x-\frac{-1-\sqrt{53}}{2})}\leq 0,& &(3^x-3)(3^x+4)>0,& &x\neq 2;& \end{cases}$

К числителю, а также ко второй скобке знаменателя опять же применяем метод замены множителей (вторая скобка знаменателя положительна, «отбрасываем» ее). Те же рассуждения – ко второй строке системы:

$\begin{cases} \frac{x-log_312}{(x-2)^2(x-log_3\frac{-1+\sqrt{53}}{2})}\leq 0,& &x>1,& &x\neq 2;& \end{cases}$

Заметим, $log_3\frac{-1+\sqrt{53}}{2}<log_39<log_312.$

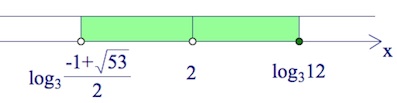
$x\in (log_3\frac{-1+\sqrt{53}}{2};2)\cup (2;log_312].$

Ответ: $(log_3\frac{-1+\sqrt{53}}{2};2)\cup (2;log_312].$

Автор: egeMax | комментария 2

Печать страницы

комментария 2

Дмитрий

2015-04-28 в 21:21

А не могли бы вы более подробно пояснить преобразования перед тем как произвести метод замены множителей?(заранее благодарю)

[ Ответить ]
- egeMax
  
  2015-04-28 в 23:26
  
  Дмитрий, применено 7 свойство логарифмов
  
  [ Ответить ]

Задание №17 Т/Р №102 А. Ларина

Добавить комментарий Отменить ответ