Задание №17 Т/Р №100 А. Ларина

Смотрите также №15,  №16, №18, №20

Решите неравенство

$log_x(\frac{100}{x})\leq \sqrt{log_x(100x^5)}$.

Решение:

$\sqrt{log_x(100x^5)}\geq log_x(\frac{100}{x});$

Совершаем равносильный переход:

$\left[\begin{array}{rcl}\begin{cases}log_x(\frac{100}{x})\geq 0,\\log_x(100x^5)\geq log^2_x(\frac{100}{x});\end{cases}\\\begin{cases}log_x(\frac{100}{x})< 0,\\log_x(100x^5)\geq 0;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}log_x100\geq 1,\\(log_x100-1)^2\leq log_x100+5;\end{cases}\\\begin{cases}log_x100<1,\\log_x100\geq -5;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}log_x100\geq 1,\\log^2_x100-3log_x100-4\leq 0;\end{cases}\\\begin{cases}log_x100<1,\\log_x100\geq -5;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}log_x100\geq 1,\\(log_x100-4)(log_x100+1)\leq 0;\end{cases}\\\begin{cases}log_x100<1,\\log_x100\geq -5;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}1\leq log_x100\leq 4,\\-5\leq log_x100<1;\end{array}\right.$

$-5\leq log_x100\leq 4;$

$\begin{cases}log_x100\leq 4,\\log_x100\geq -5;&\end{cases}$

Далее решаем методом рационализации:

$\begin{cases}(x-1)(100-x^4)\leq 0,\\(x-1)(100-\frac{1}{x^5})\geq 0,\\x>0,\\x\neq 1;&\end{cases}$

$\begin{cases}(x-1)(\sqrt{10}-x)(\sqrt{10}+x)\leq 0,\\x(x-1)(x-\frac{1}{\sqrt[5]{100}})\geq 0,\\x>0,\\x\neq 1;&\end{cases}$

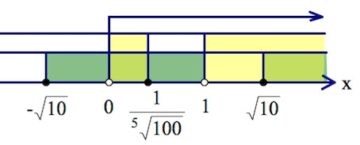
$x\in (0;\frac{1}{\sqrt[5]100}]\cup [\sqrt{10};+\infty).$

Ответ: $(0;\frac{1}{\sqrt[5]100}]\cup [\sqrt{10};+\infty).$