Задание №16 Т/Р №100 А. Ларина

Смотрите также  №15, №17, №18, №20
В правильной четырехугольной пирамиде $SABCD$ длина высоты, опущенной из вершины $S$ на основание $ABCD$, равна $6\sqrt2$. Через точку касания с боковой гранью $SAB$ вписанного в эту пирамиду шара параллельно прямой $AB$ проведена плоскость, проходящая через ближайшую к вершине $S$ точку шара.
а) Постройте сечение пирамиды этой плоскостью.
б) Найдите площадь сечения, если $AB=4\sqrt6.$

Решение:

a) Пусть $K$ – точка касания шара с боковой гранью пирамиды $SAB.$

Плоскость сечения, параллельная по условию $AB$, пересекает плоскость грани $SAB$ по прямой ($l$), параллельной $AB$.

Пусть $l$ пересекает $AS$, $BS$ соответственно в точках $M$ и $N$.

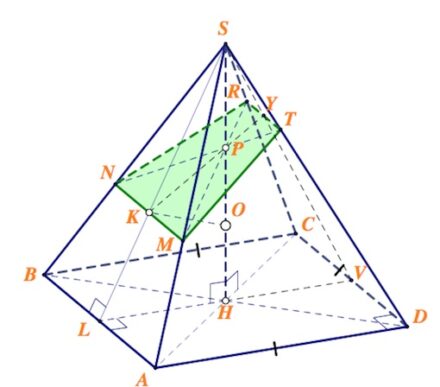
Плоскость сечения проходит через ближайшую к вершине точку шара, назовем ее $P$ ($P\in SH$, $H$  – проекция $S$ на плоскость основания $ABCD$). Точки $M$ и $P$ лежат в плоскости $ACS$. Тогда $MP$ пересекается с $SC$ в некоторой точке, назовем ее $R$.

Аналогично,точки $N$ и $P$ лежат в плоскости $BSD$. Тогда $NP$ пересекается с $SD$ в некоторой точке, назовем ее $T$.

Четырехугольник $MNRT$ – искомое сечение.

Заметим, $MNRT$ – трапеция. (Действительно, $CD$, будучи параллельной $AB$, которая в свою очередь параллельна плоскости сечения, параллельна плоскости сечения. А значит, плоскость сечения пересекает плоскость $SDC$, в которой лежит $CD$ по прямой, параллельной $CD$). Очевидно также, что  $MNRT$ – равнобедренная трапеция.

б) Заметим, точка $K$ лежит на высоте ($SL$) треугольника $SAB$. (Действительно, наклонная $SO$ к плоскости $SAB$ перпендикулярна $AB$, значит и ее проекция $SK$ на плоскость $SAB$  перпендикулярна $AB$ по теореме о трех перпендикулярах). При этом, очевидно, $K$ – середина $MN.$

Пусть $SV\perp CD$.

Треугольник $SLV$  – равносторонний. Действительно, $LV=4\sqrt6$  и $SL=SV=\sqrt{(6\sqrt2)^2+(2\sqrt6)^2}=4\sqrt6.$

В равносторонний треугольник $SLV$ вписана окружность. $OH=\frac{1}{3}SH=2\sqrt2.$  Также и $OK=OP=PS=2\sqrt2.$

Из прямоугольного треугольника $KSO$ медиана $KP$, проведенная к гипотенузе, – половина гипотенузы, то есть $2\sqrt2.$

Треугольник $KPO$ – равносторонний. Тогда угол $SPY=60^{\circ}.$ А поскольку угол $PSY=30^{\circ}$ ($Y$ – точка пересечения $KP$ и $SV$ ), то $KY\perp SV.$

Имеем: $PY=\frac{SP}{2}=\sqrt2,$ $SY=\sqrt{SP^2-PY^2}=\sqrt6.$

Из подобия треугольников $MSN$ и $ASB$:

  $MN:AB=SK:SL,$ то есть $MN=\frac{AB}{2}=2\sqrt6.$

Из подобия треугольников $TSR$ и $DSC$:

$TR:DC=SY:SV,$ то есть $TR=\frac{AB}{4}=\sqrt6.$

Из подобия треугольников $KPN$ и $YPT$:

$KP:PY=MN:TR,$ то есть $PY=\frac{KP}{2}=\sqrt2.$

Наконец, $S_{MNRT}=\frac{MN+RT}{2}\cdot KY=\frac{2\sqrt6+\sqrt6}{2}\cdot 3\sqrt2=9\sqrt3.$

Ответ: $9\sqrt3.$