Главная › 16 (С5) Планиметр. задачи › Задание №18 (С4) из Т/Р №91 А. Ларина

13 Ноя 2014

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

Задание №18 (С4) из Т/Р №91 А. Ларина

Елена Репина 2014-11-13 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15, №16, №17, №20.

В равнобедренном треугольнике $ABC$ $AC$ – основание. На продолжении стороны $CB$ за точку $B$ отмечена точка $D$ так, что угол $CAD$ равен углу $ABD$ .

а) Докажите, что $AB$ – биссектриса угла $CAD$ .

б) Найдите длину отрезка $AD$ , если боковая сторона треугольника $ABC$ равна 5, а его основание равно 6.

Решение:

a)

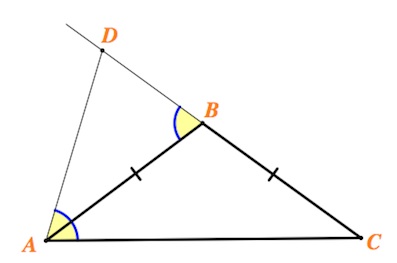
Если принять угол при основании равнобедренного треугольника $ABC$ за $\alpha$ , то угол $ABD$ , как внешний угол треугольника, будет равен $2\alpha$ .

ббь

А поскольку по условию углы $CAD$ и $ABD$ равны, то становится очевидным, что и угол $DAB$ , как и угол $BAC$ , равен $\alpha$ , то есть $AB$ – биссектриса угла $CAD.$

б)

Треугольники $ABD$ и $CAD$ подобны по двум углам ( $\angle ABD= \angle CAD$ , $\angle DAB=\angle DCA$ ), значит

$\frac{AB}{AC}=\frac{BD}{AD}=\frac{AD}{CD};$

Так как по условию $AB=5,$ $AC=6$ , то

$\frac{5}{6}=\frac{BD}{AD}=\frac{AD}{5+BD}.$

Из $\frac{5}{6}=\frac{BD}{AD}$ имеем: $BD=\frac{5AD}{6}.$

Возвращаемся в следующую пропорцию:

$\frac{5}{6}=\frac{AD}{5+BD}$ :

$\frac{5}{6}=\frac{AD}{5+\frac{5AD}{6}};$

$5(30+5AD)=36AD;$

$150+25AD=36AD;$

$11AD=150;$

$AD=\frac{150}{11}.$

Ответ: $\frac{150}{11}.$

Автор: egeMax | Нет комментариев

Печать страницы

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы