Главная › 13 (С2) Стереометр. задачи › Задание №16 (С2) из Т/Р №91 А. Ларина

13 Ноя 2014

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

Задание №16 (С2) из Т/Р №91 А. Ларина

Елена Репина 2014-11-13 2016-06-10

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №20.

На боковых ребрах $AA_1$ , $BB_1$ и $CC_1$ правильной треугольной призмы $ABCA_1B_1C_1$ ( $AA_1|| BB_1|| CC_1$ ) расположены точки $K$ , $L$ , и $M$ соответственно. Известно, что угол между прямыми $KL$ и $AB$ равен $\frac{\pi}{4}$ , а угол между прямыми $KM$ и $AC$ – $\frac{\pi}{3}$ .

а) Постройте плоскость, проходящую через точки $K$ , $L$ и $M$ ;

б) Найдите угол между этой плоскостью и плоскостью основания $ABC.$

Решение:

б) Будем искать угол между плоскостями $KLM$ и $ABC$ , опираясь на формулу $S_{proeksia}=S_{sechenie}\cdot cos\alpha$ , где $\alpha$ – угол между плоскостями сечения и основания.

В нашем случае $S_{ABC}=S_{KLM}\cdot cos\alpha.$

льт

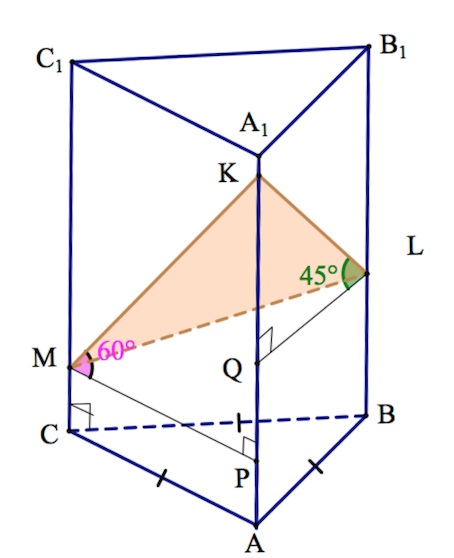
Примем сторону основания $ABC$ (правильного треугольника) за $a$ .

Тогда $S_{ABC}=\frac{a^2\sqrt3}{4}$ .

Найдем площадь треугольника $KML$ . Но прежде найдем все его стороны.

Угол между прямыми $KM$ и $AC$ – это угол $KMP$ , где $MP||AC.$

Угол между прямыми $KL$ и $AB$ – это угол $KLQ$ , где $LQ||AB.$

Из прямоугольного треугольника $KMP$ ( $\angle M=60^{\circ}$ , $MP=a$ ): $MK=2MP=2a$ .

Из прямоугольного треугольника $KLQ$ ( $\angle L=45^{\circ}$ , $QL=a$ ): $KL=a\sqrt2$ .

Пусть $PE||AB$ , $E\in BB_1$ .

Обратимся к треугольнику $MLE$ : $LE=KP-KQ=a\sqrt3-a$ , $ME=a$ .

Тогда по теореме Пифагора

$ML=\sqrt{a^2+a^2(\sqrt3-1)^2}=a\sqrt{5-2\sqrt3}.$

По теореме косинусов для треугольника $MLK$ :

$ML^2=MK^2+KL^2-2MK\cdot KL\cdot cosMKL;$

$a^2(5-2\sqrt3)=4a^2+2a^2-4\sqrt2a^2cosMKL;$

$cosMKL=\frac{1+2\sqrt3}{4\sqrt2};$

Тогда $sinMKL=\sqrt{1-(\frac{1+2\sqrt3}{4\sqrt2})^2}=\frac{\sqrt{19-4\sqrt3}}{4\sqrt2}.$

Мы готовы вычислить площадь треугольника $MKL$ :

$S_{MKL}=\frac{1}{2}\cdot MK\cdot KL\cdot sin MKL;$

$S_{MKL}=\frac{1}{2}\cdot 2a\cdot a\sqrt2\cdot \frac{\sqrt{19-4\sqrt3}}{4\sqrt2};$

$S_{MKL}=\frac{a^2\sqrt{19-4\sqrt3}}{4};$

Наконец,

$cos\alpha=\frac{S_{ABC}}{S_{MKL}}=\frac{\frac{a^2\sqrt3}{4}}{\frac{a^2\sqrt{19-4\sqrt3}}{4}}=\sqrt{\frac{3}{19-4\sqrt3}}.$

$\alpha=arccos\sqrt{\frac{3}{19-4\sqrt3}}.$

Следует отметить, что возможен и такой случай: длот

Рассуждая аналогично, получим, что искомый угол – $arccos\sqrt{\frac{3}{19+4\sqrt3}}$

Ответ: $arccos\sqrt{\frac{3}{19\pm 4\sqrt3}}.$

Автор: egeMax | комментария 2

Печать страницы

комментария 2

Дима

2015-03-25 в 21:56

А разве не нужно писать то, как построена плоскость?? То есть весь пункт А

[ Ответить ]
- egeMax
  
  2015-03-25 в 21:59
  
  А что там писать-то?.. Самый простой случай…
  
  [ Ответить ]

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы