Задание №15 (С1) из Т/Р №91 А. Ларина

Смотрите также №16, №17, №18, №20

a) Решите уравнение $4sin^2x+4cos(\frac{\pi}{2}+x)=3sin\frac{\pi}{2}.$

б) Укажите корни этого уравнения, принадлежащие интервалу $(-\frac{3\pi}{2};3\pi).$

Решение:

a)

$4sin^2x+4cos(\frac{\pi}{2}+x)=3sin\frac{\pi}{2};$

$4sin^2x-4sinx-3=0;$

$\left[\begin{array}{rcl}sinx=\frac{4+8}{8},\\sinx=\frac{4-8}{8};\end{array}\right.$

$sinx=-\frac{1}{2};$

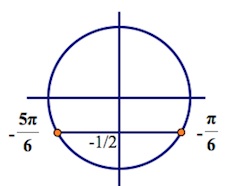
$\left[\begin{array}{rcl}x=-\frac{\pi}{6}+2\pi  n, n\in Z,\\x=-\frac{5\pi}{6}+2\pi n, n\in Z;\end{array}\right.$

б) Отбор корней уравнения из интервала $(-\frac{3\pi}{2};3\pi)$ производим при помощи тригонометрического круга:

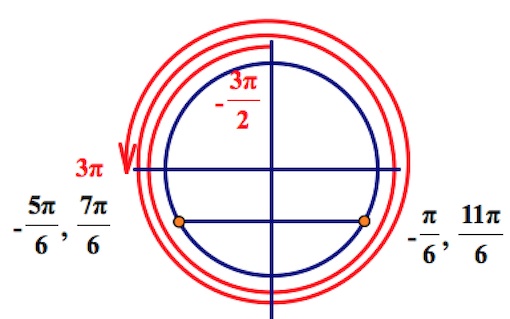
Ответ:

a) $-\frac{\pi}{6}+2\pi  n,  -\frac{5\pi}{6}+2\pi  n, n\in Z;$

б) $-\frac{5\pi}{6}, -\frac{\pi}{6}, \frac{7\pi}{6}, \frac{11\pi}{6}.$