Главная › 17 (С6) Параметры* › Задание №20 (С5) из Т/Р №91 А. Ларина

13 Ноя 2014

Категория: 17 (С6) Параметры*Т/P A. Ларина

Задание №20 (С5) из Т/Р №91 А. Ларина

Елена Репина 2014-11-13 2016-07-12

В новом формате ЕГЭ по математике задание значится как «Задание №18»

Смотрите также №15, №16, №17, №18.

Найдите все значения $a$ , при каждом из которых функция $f(x)=||x|-2|-ax+8a$ принимает значение, равное 2, в двух различных точках.

Решение:

Найдем все значения $a$ , при которых уравнение $||x|-2|=ax-8a+2$ имеет два различных решения.

Привожу лишь краткое решение.

График левой части:

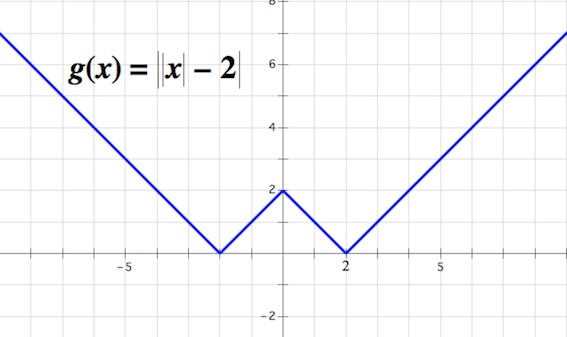
График правой части – семейство прямых, проходящих через точку $(8;2):$

лот

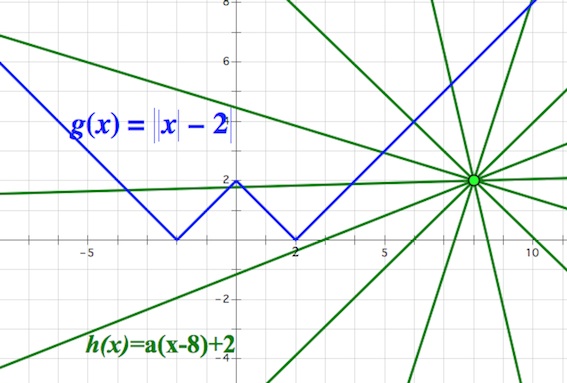
При тех $a$ , что отвечают за расположение прямых $h(x)=a(x-8)+2$ внутри зоны, выделенной на рисунке зеленым цветом, графики $g(x)$ и $h(x)$ пересекаются в двух различных точках.

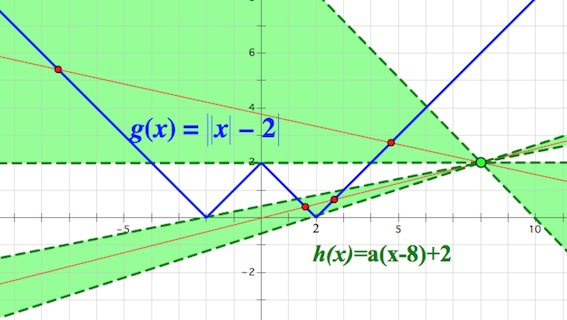
Несложно найти значения $a$ , отвечающие за расположение прямых $h(x)=a(x-8)+2$ на границах выделенной зоны.

Например, когда прямая $h(x)=a(x-8)+2$ проходит через точку $A(2;0)$ значение $a$ будет равно $\frac{1}{3}$ , так как $0=a(2-8)+2$ (подставили координаты точки $A$ в $h(x)=a(x-8)+2$ ).

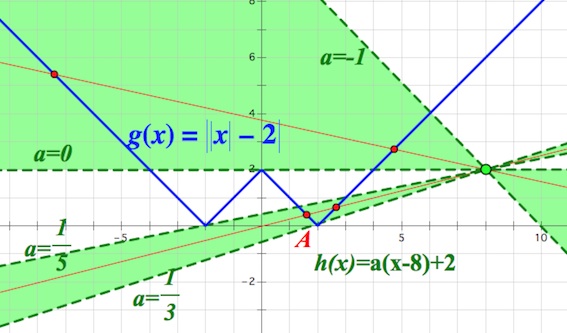
Опускаем подробности. Приходим к тому, что устраивающие нас значения $a$ таковы:

$(-1;0)\cup(\frac{1}{5};\frac{1}{3}).$

Ответ: $(-1;0)\cup(\frac{1}{5};\frac{1}{3}).$

Автор: egeMax | Нет комментариев

Печать страницы

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы