Главная › 14 (С3) Неравенства › Задание №17 (С3) Т/Р №97 А. Ларина

25 Дек 2014

Категория: 14 (С3) НеравенстваЛогарифмыТ/P A. Ларина

Задание №17 (С3) Т/Р №97 А. Ларина

Елена Репина 2014-12-25 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №15»

Решите неравенство: $log_3(x+6)\leq (1-log_{9x}(6-x))\cdot log_3(9x).$

Решение:

$log_3(x+6)\leq (1-log_{9x}(6-x))\cdot log_3(9x);$

Производим раскрытие скобок в левой части неравенства:

$log_3(x+6)\leq log_3(9x)-log_{9x}(6-x)\cdot log_3(9x);$

Применяем свойство №7 логарифмов ко второму слагаемому левой части неравенства:

$log_3(x+6)\leq log_3(9x)-log_3(6-x);$

Применяем свойство №4 логарифмов к левой части неравенства, следя за равносильностью переходов (достаточно указать что-то одно – либо $9x>0$ , либо $6-x>0$ ):

$\begin{cases} log_3(x+6)\leq log_3\frac{9x}{6-x},& &x>0;& \end{cases}$

$\begin{cases} x+6\leq \frac{9x}{6-x},& &x>0;& \end{cases}$

$\begin{cases} \frac{9x-(6+x)(6-x)}{6-x}\geq 0,& &x>0;& \end{cases}$

$\begin{cases} \frac{x^2+9x-36}{6-x}\geq 0,& &x>0;& \end{cases}$

$\begin{cases} \frac{(x-3)(x+12)}{6-x}\geq 0,& &x>0;& \end{cases}$

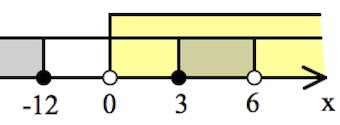
$x\in [3;6).$

Ответ: $[3;6).$

Автор: egeMax | Нет комментариев

Печать страницы

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (12)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (79)
- 13 (С2) Стереометр. задачи (95)
- 14 (С3) Неравенства (90)
- 15 (С4) Практич. задачи (72)
- 16 (С5) Планиметр. задачи (87)
- 17 (С6) Параметры* (80)
- 18 (С7) Числа, их свойства (39)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Задачи (28)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (59)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы