Задание №17 (С3) из Т/Р №91 А. Ларина

Смотрите также №15, №16, №18, №20

Решите неравенство: $log_2(5-x)\cdot log_{x+1}\frac{1}{8}\geq -6.$

Решение:

Помня о свойстве $\color{red}log_ab=\frac{1}{log_ba}$, переходим к следующему неравенству:

 $log_2(5-x)\cdot \frac{1}{log_{\frac{1}{8}}(x+1)}\geq -6;$

Помня о свойстве $\color{red}log_{a^n}b=\frac{1}{n}{log_ab}$  и понимая, что $\frac{1}{8}=2^{-3}$, переходим к следующему неравенству:

$log_2(5-x)\cdot \frac{1}{-\frac{1}{3}log_{2}(x+1)}\geq -6$

или

$-\frac{3log_2(5-x)}{\log_{2}(x+1)}\geq -6,$

а затем

$\frac{log_2(5-x)}{\log_{2}(x+1)}\leq 2.$

Помня о свойстве $\color{red}log_ab=\frac{log_cb}{log_ca}$, переходим к следующему неравенству:

$log_{x+1}(5-x)\leq 2,$

решать которое будем методом рационализации:

$\begin{cases}(x+1-1)(5-x-(x+1)^2)\leq 0,\\x+1>0,\\x+1\neq 1,\\5-x>0;\end{cases}$

$\begin{cases}x(x-1)(x+4)\geq 0,\\x>-1,\\x\neq 0,\\x<5;\end{cases}$

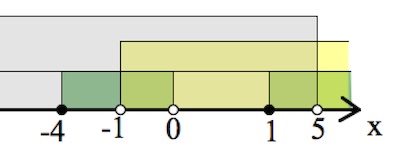
Ответ: $(-1;0)\cup [1;5).$