Главная › Справочные материалы › Вектора на плоскости. Часть 2

24 Авг 2013

Категория: Справочные материалы

Вектора на плоскости. Часть 2

Елена Репина 2013-08-24 2014-08-20

Координаты вектора

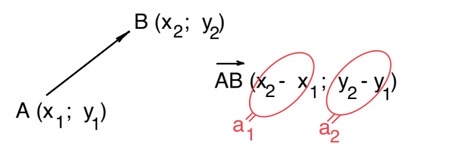
Пусть вектор $\vec{a}$ имеет началом точку $A_1(x_1;y_1)$ , а концом – точку $A_2(x_2;y_2)$ . Координатами вектора $\vec{a}$ называются числа $a_1=x_2-x_1,\;a_2=y_2-y_1$ . Обозначают так: $\vec{a}(a_1;a_2).$

координаты вектора

Координаты нулевого вектора равны нулю.

Длина вектора (или абсолютная величина вектора) $\vec{a}(a_1;a_2)$ выражается формулой

$|\vec{a}|=\sqrt{a_1^2+a_2^2}.$

Равные векторы имеют равные соответствующие координаты.

И наоборот. Если у векторов соответствующие координаты равны, то векторы равны.

Сложение векторов

Суммой векторов $\vec{a}(a_1;a_2)$ и $\vec{b}(b_1;b_2)$ называется вектор $\vec{c}$ с координатами $(a_1+b_1,\;a_2+b_2).$

Умножение вектора на число

Произведением вектора $(\vec{a_1;a_2})$ на число $\lambda$ называется вектор $\vec{(\lambda a_1;\lambda a_2)}$ , то есть

$\lambda \vec{(a_1;a_2)}=\vec{(\lambda a_1;\lambda a_2)}$

Коллинеарные вектора

Пусть $\vec{a}$ и $\vec{b}$ – отличные от нуля коллинеарные векторы. Тогда существует число $\lambda$ такое, что

$\vec{b}=\lambda \vec{a}$

Угол между векторами

Углом между любыми двумя ненулевыми векторами $\vec{a}$ и $\vec{b}$ называется угол между равными им векторами с общим началом (наименьший угол).

угол между векторами

Угол между двумя векторами находится в промежутке $[0^{\circ};180^{\circ}]$ .

Угол между одинаково направленными векторами равен нулю.

Скалярное произведение векторов

I. Скалярным произведением векторов $\vec{a}(a_1;a_2)$ и $\vec{b}(b_1;b_2)$ называется число $a_1b_1+a_2b_2$ , то есть

$\vec{a}\cdot \vec{b}=a_1b_1+a_2b_2$

II. Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними, то есть

$\vec{a}\cdot \vec{b}=|\vec{a}|\cdot |\vec{b}|\cdot cos\angle (\vec{a};\vec{b})$

Следовательно, если векторы перпендикулярны, то их скалярное произведение равно нулю. Верно и обратное.

Из формул I и II скалярного произведения вытекает, что угол между векторами можно найти, используя формулу:

$cos\angle (\vec{a};\vec{b})=\frac{\vec{a}\cdot \vec{b}}{|\vec{a}|\cdot |\vec{b}|}=\frac{a_1b_1+a_2b_2}{\sqrt{a_1^2+a_2^2}\sqrt{b_1^2+b_2^2}}$

Также, следствием, например, формулы II скалярного произведения есть следующий важный момент:

$\vec{a}^2=|\vec{a}|^2$

Автор: egeMax | комментария 4

Печать страницы

комментария 4

Анатолий

2014-02-18 в 15:45

что касается этой темы, я поймал себя на мысли что изучил её, но через неделю всё напрочь забыл, ибо вообще ничего не понял, а без понимания не возможно запомнить…

[ Ответить ]
- egeMax
  
  2014-02-18 в 21:29
  
  «без понимания невозможно запомнить…»
  Истину глаголишь!
  Закрепляем изученный материал решением задач: 1, 2
  
  [ Ответить ]
  - Анатолий
    
    2014-02-18 в 23:57
    
    обязательно :) вернусь к этим темам когда дойду до 15, а затем уже и часть С начну осваивать… ;)
    
    [ Ответить ]
    - egeMax
      
      2014-02-19 в 00:01
      
      Правильно!
      
      [ Ответить ]