Вектора. Часть 1

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Вектором называется направленный отрезок  $\vec{AB}$, где точка $A$ – начало, точка $B$ – конец вектора.

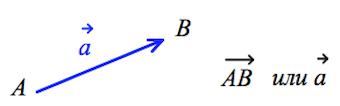
Нулевым вектором   $\vec{o}$ называется вектор, у которого начало совпадает с концом.

Векторы $\vec{AB}$ и $\vec{CD}$ называются одинаково направленными или сонаправленными, если лучи AB и CD одинаково направлены.

Если лучи AB и CD противоположно направлены, векторы $\vec{AB}$ и $\vec{CD}$ называются противоположно направленными.

Два вектора называются коллинеарными , если они лежат на одной прямой или на параллельных прямых.

Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютную величину вектора $\vec{a}$ обозначают $|\vec{a}|$.

Два вектора называются равными, если они одинаково направлены и равны по абсолютной величине.

Два вектора с равными модулями, лежащие на параллельных прямых, но противоположно направленные, называются противоположными. Вектор, противоположный вектору $\vec{a}$, обозначается как $-\vec{a}$.

СЛОЖЕНИЕ ВЕКТОРОВ

Сложение векторов $\vec{a}$  и $\vec{b}$  по правилу треугольника

Суммой $\vec{a}+\vec{b}$  двух векторов $\vec{a}$  и $\vec{b}$ называют такой третий вектор $\vec{c}$, начало которого совпадает с началом $\vec{a}$, а конец – с концом  $\vec{b}$ при условии, что конец вектора $\vec{a}$  и начало вектора $\vec{b}$  совпадают.

Сложение векторов $\vec{a}$  и $\vec{b}$  по правилу параллелограмма

Если два неколлинеарных вектора $\vec{a}$  и $\vec{b}$  привести к общему началу, то вектор $\vec{c}=\vec{a}+\vec{b}$  совпадает с диагональю параллелограмма, построенного на векторах $\vec{a}$  и $\vec{b}$. Причем начало вектора $\vec{c}$ совпадает с началом заданных векторов.

Разностью $\vec{a}-\vec{b}$ векторов  и  называется вектор $\vec{c}$  такой, что выполняется условие: $\vec{b}+\vec{c}=\vec{a}$.

Смотрите также «Вектора. Часть 2».