Стоит ли учить формулы приведения?
Вы в состоянии выучить вот такую таблицу? :(
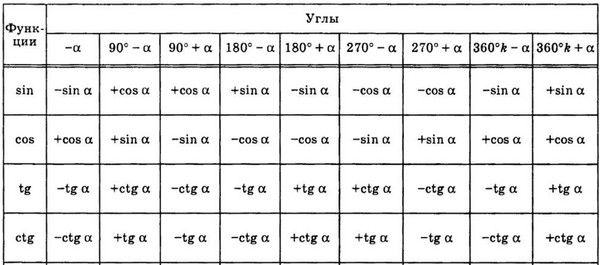
А без приведения сложных аргументов тригонометрических функций к аргументам первой четверти на ЕГЭ по математике никуда.
Но нет необходимости учить эту таблицу!
Нужно просто потратить немного времени и понять алгоритм применения формул приведения.
Не будем терять время! Поехали!
Зачем вообще формулы приведения?
Формулы приведения позволяют упростить вычисления, привести сложные аргументы тригонометрических функций к аргументам I четверти.
Вот, например, типичное задание из ЕГЭ по математике:
Вычислите $sin2130^{\circ}$ или $\sqrt2cos\frac{21\pi}{4}.$
Давайте разбираться. А к примерам вернемся чуть позже.
Если хотите докапаться до самой сути, то –> + показать
Медленно, но верно. Далее сформулируем правило
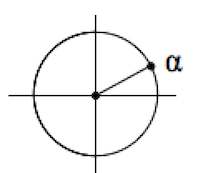
Пример 1. Упростим $sin(\pi+\alpha)$.
Считаем $\alpha$ – углом первой четверти!
Отмечаем углы $\alpha$, $\pi+\alpha$:
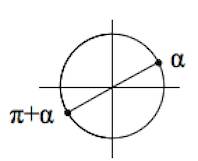
Отмечаем значения $sin(\pi+\alpha)$ и $sin\alpha$:
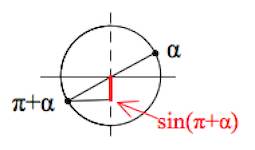
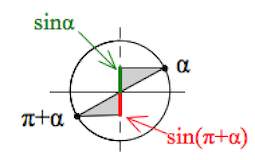
Очевидно, длина «зеленого» катета равна длине «красного» в силу равенства «серых» треугольников:
Но только $sin(\pi+\alpha)$ – отрицательная величина, а $sin\alpha$ – положительная.
Поэтому $\color{red}sin(\pi+\alpha)=-sin\alpha.$
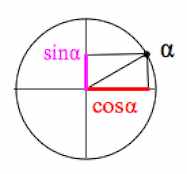
Пример 2. Упростим $cos(\frac{3\pi}{2}-\alpha)$.
Вот $cos\alpha$ и $sin\alpha$:
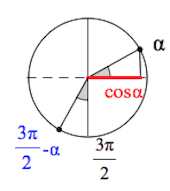
Вот $\frac{3\pi}{2}-\alpha$:
И вот $cos(\frac{3\pi}{2}-\alpha)$:
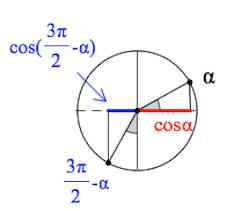
Из следующей картинки хорошо видно, что длина отрезка, помеченного синим цветом, равна длине отрезка, помеченного зеленым цветом.
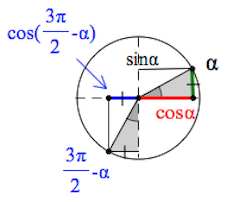
При этом $cos(\frac{3\pi}{2}-\alpha)$ – отрицательная величина, $sin\alpha$ – положительная.
Поэтому $\quicklatex{color=”red”}cos(\frac{3\pi}{2}-\alpha)=-sin\alpha.$
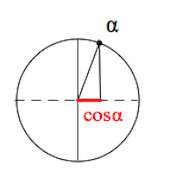
Пример 3. Упростим $cos(2\pi-\alpha)$.
Вот $cos\alpha$:
Значение же $cos(2\pi-\alpha)$, как хорошо видно на картинке, то же, что и $cos\alpha:$
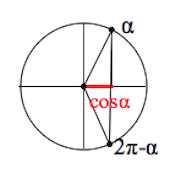
Поэтому $\quicklatex{color=”red”}cos(2\pi-\alpha)=cos\alpha$.
Можно разбирать примеры и дальше для более четкого выявления закономерностей, но давайте уже сформулируем правило, на которое будем опираться при работе с формулами приведения.
Вы всегда сможете проверить «правильность» формулы способом, который мы только что применяли.
Мнемоническое правило для формул приведения
1. Задаем себе вопрос: «Меняется ли название функции на кофункцию?» + показать
(то есть синнус на косинус, косинус на синус, тангенс на котангенс и котангенс на тангенс).
Чтобы ответить на этот вопрос нужно, не смейтесь, – подвигать головой вдоль оси, на которой располагается ключевая точка. Ключевые точки всегда располагаются здесь (см. рис.):
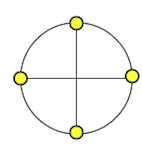
Например, в формулах $sin(\frac{3\pi}{2}+\alpha),\;cos(10\pi+\alpha),\;tg(\frac{5\pi}{2}+30^{\circ})$ – ключевые точки – это $\frac{3\pi}{2},\;10\pi,\;\frac{5\pi}{2}$.
Так вот если вы мотаете головой вдоль горизонтальной прямой, потому что ключевая точка располагается на ней, то вы, как бы, отвечаете «нет» на вопрос «Меняется ли название функции на кофункцию?»
Если вы киваете головой вдоль вертикальной прямой, потому что ключевая точка располагается на ней, то вы отвечаете «да» на вопрос «Меняется ли название функции на кофункцию?».
2. Ставим справа, на выходе, тот знак, какой несет в себе левая, исходная, часть.
Данное правило еще называется «лошадиным».
Примеры
При выполнении заданий нам понадобятся основные значения тригонометрических функций
Пример 1. Вычислить $sin2130^{\circ}$. + показать
Решение:
1. $sin2130^{\circ}=sin(360^{\circ}\cdot 6-30^{\circ})$
Ключевая точка $360^{\circ}\cdot 6$ располагается на горизонтальной оси:
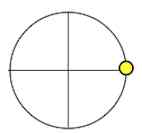
Название функции меняться не будет.
2. Исходное значение $sin2130^{\circ}$ – отрицательно, так как располагается в IV четверти:
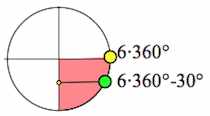
Итак, $sin2130^{\circ}=-sin30^{\circ}=-0,5.$
Ответ: $-0,5.$
Пример 2. Вычислить $\sqrt2cos\frac{21\pi}{4}.$ + показать
Решение:
1. $\sqrt2cos\frac{21\pi}{4}=\sqrt2cos(\frac{20\pi}{4}+\frac{\pi}{4})=\sqrt2cos(5\pi+\frac{\pi}{4})$
Ключевая точка $5\pi$ располагается на горизонтальной оси:
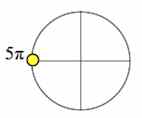
Название функции меняться не будет.
2. Исходное значение $\sqrt2cos\frac{21\pi}{4}$ – отрицательно, так как располагается в III четверти:
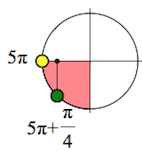
Итак,
$\sqrt2cos\frac{21\pi}{4}=-\sqrt2cos\frac{\pi}{4}=-\sqrt2\cdot \frac{\sqrt2}{2}=-1.$
Ответ: $-1.$
Пример 3. Упростить $\frac{cos(\alpha+\pi)sin(\frac{\pi}{2}-\alpha)-cos^2(\frac{\pi}{2}-\alpha)}{tg(\alpha-\pi)sin(\frac{\pi}{2}+\alpha)}.$ + показать
Решение:
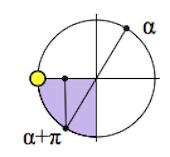
$cos(\alpha+\pi)=-cos\alpha$ (название не меняем, знаки $cos(\alpha+\pi)$ и $cos\alpha$ различаются, как видим из картинки, – ставим справа знак «-»)
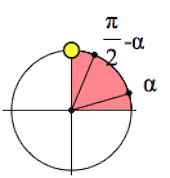
$sin(\frac{\pi}{2}-\alpha)=cos\alpha$ (название меняем, знаки $sin(\frac{\pi}{2}-\alpha)$ и $cos\alpha$, как видно из картинки, одинаковы, – ставим справа знак «+»)
$cos^2(\frac{\pi}{2}-\alpha)=sin^2\alpha$ (название меняем, проверять знак нет необходимости, так как все равно у нас функция – в квадрате)
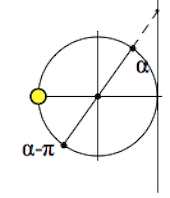
$tg(\alpha-\pi)=tg\alpha$ (название не меняем, знаки $tg(\alpha-\pi)$ и $tg\alpha$, как видно из картинки, одинаковы, ставим справа знак «+»)
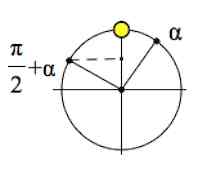
$sin(\frac{\pi}{2}+\alpha)=cos\alpha$ (название меняем, знаки $sin(\frac{\pi}{2}+\alpha)$ и $cos\alpha$, как видно из картинки, одинаковы, ставим справа знак «+» )
Итак,
$\frac{cos(\alpha+\pi)sin(\frac{\pi}{2}-\alpha)-cos^2(\frac{\pi}{2}-\alpha)}{tg(\alpha-\pi)sin(\frac{\pi}{2}+\alpha)}=\frac{-cos\alpha\cdot cos\alpha-sin^2\alpha}{tg\alpha \cdot cos\alpha}=\frac{-1}{sin\alpha}.$
Ответ: $-\frac{1}{sin\alpha}.$






















Спасибо, здесь всё очень понятно и доступно ;)
Просто замечательный сайт=)
Спасибо!
Ваш сайт – один из самых лучших! Спасибо!!!
Мария, спасибо!
Все понятно, примеры информативные. Спасибо!
исправьте орф. ошибки в “мнемоническом правиле”, тангенсТ и пр.
в целом сайт 5+