Главная › Справочные материалы › Квадратичная функция

19 Май 2013

Категория: Справочные материалыФункции и графики

Квадратичная функция

Елена Репина 2013-05-19 2021-10-17

Функция вида $y=ax^2+bx+c$ , где $a\neq 0$ называется квадратичной функцией.

График квадратичной функции – парабола.

парабола, построение параболы, график парабола

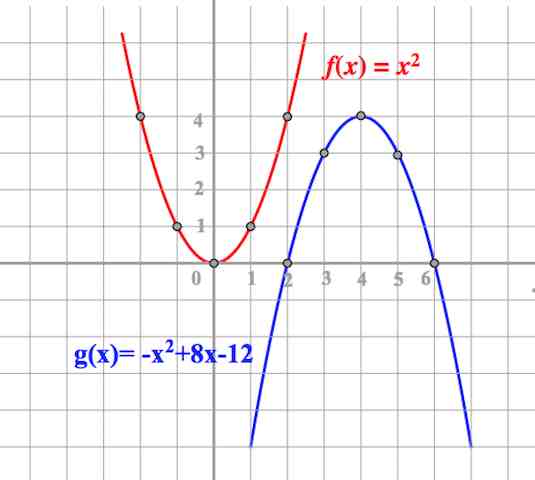
Рассмотрим случаи:

I СЛУЧАЙ, КЛАССИЧЕСКАЯ ПАРАБОЛА

$y=x^2$ , то есть $a=1$ , $b=0$ , $c=0$

Для построения заполняем таблицу, подставляя значения x в формулу:

parabola2

Отмечаем точки (0;0); (1;1); (-1;1) и т.д. на координатной плоскости (чем с меньшим шагом мы берем значения х ( в данном случае шаг 1 ), и чем больше берем значений х, тем плавнее будет кривая), получаем параболу:

классическая парабола, парабола, построение параболы

Нетрудно заметить, что если мы возьмем случай $a=-1$ , $b=0$ , $c=0$ , то есть $y=-x^2$ , то мы получим параболу, симметричную $y=x^2$ относительно оси (ох). Убедиться в этом несложно, заполнив аналогичную таблицу:

парабола, построение параболы

II СЛУЧАЙ, «a» ОТЛИЧНО ОТ ЕДИНИЦЫ

Что же будет, если мы будем брать $a=2$ , $a=-3$ , $a=0.5$ ? Как изменится поведение параболы? При $|a|>1$ парабола $y=ax^2$ изменит форму, она “похудеет” по сравнению с параболой $y=x^2$ (не верите – заполните соответствующую таблицу – и убедитесь сами):

парабола, построение параболы, ветви параболы, коэффициенты параболы, дискриминант

На первой картинке (см. выше) хорошо видно, что точки из таблицы для параболы $y=x^2$ (1;1), (-1;1) трансформировались в точки (1;4), (1;-4), то есть при тех же значениях $x$ ордината $y$ каждой точки умножилась на 4. Это произойдет со всеми ключевыми точками исходной таблицы. Аналогично рассуждаем в случаях картинок 2 и 3.

А при $|a|<1$ парабола $y=ax^2$ «станет шире» параболы $y=x^2$ :

парабола, построение параболы, ветви параболы, коэффициенты параболы, дискриминант, ветви вниз

Давайте подитожим:

1) Знак коэффициента $a$ отвечает за направление ветвей. При $a > 0$ ветви направлены вверх, при $a < 0$ — вниз.

2) Абсолютная величина коэффициента (модуля) $a$ отвечает за “расширение”, “сжатие” параболы. Чем больше $|a|$ , тем у’же парабола, чем меньше |a|, тем шире парабола.

III СЛУЧАЙ, ПОЯВЛЯЕТСЯ «С»

Теперь давайте введем в игру $c$ (то есть рассматриваем случай, когда $c\neq 0$ ), будем рассматривать параболы вида $y=ax^2+c$ . Нетрудно догадаться (вы всегда можете обратиться к таблице), что будет происходить смещение параболы $y=ax^2$ вдоль оси $(oy)$ вверх или вниз в зависимости от знака $c$ :

парабола, построение параболы, сдвиг параболы, ветви параболы, коэффициенты параболы, дискриминант

IV СЛУЧАЙ, ПОЯВЛЯЕТСЯ «b»

Когда же парабола “оторвется” от оси $(oy)$ и будет, наконец, “гулять” по всей координатной плоскости? Когда $b$ перестанет быть равным $0$ .

Здесь для построения параболы $y=ax^2+bx+c$ нам понадобится формула для вычисления вершины: $x_o=\frac{-b}{2a}$ , $y_o=y(x_o)$ .

Так вот в этой точке (как в точке (0;0) новой системы координат) мы будем строить параболу $y=ax^2$ , что уже нам по силам. Если имеем дело со случаем $a=1$ , то от вершины откладываем один единичный отрезок вправо, один вверх, – полученная точка – наша (аналогично шаг влево, шаг вверх – наша точка); если имеем дело с $a=2$ , например, то от вершины откладываем один единичный отрезок вправо, два – вверх и т.д.

Например, вершина параболы $y=x^2-4x-2$ :

$x_o=\frac{4}{2}=2$ , $y_o=(2)^2-4\cdot 2 -2=-6$ . Теперь главное уяснить, что в этой вершине мы будем строить параболу по шаблону параболы $y=x^2$ , ведь $a=1$ в нашем случае.

парабола, построение параболы, ветви параболы, дискриминант

При построении параболы после нахождения координат вершины очень удобно учитывать следующие моменты:

1) парабола обязательно пройдет через точку $(0;c)$ . Действительно, подставив в формулу $y=ax^2+bx+c$ x=0, получим, что $y=c$ . То есть ордината точки пересечения параболы с осью (оу), это $c$ . В нашем примере (выше), парабола пересекает ось ординат в точке $-2$ , так как $c=-2$ .

2) осью симметрии параболы является прямая $x=\frac{-b}{2a}$ , поэтому все точки параболы будут симметричны относительно нее. В нашем примере, мы сразу берем точку (0; -2) и строим ей симметричную относительно оси симметрии параболы, получим точку (4; -2), через которую будет проходить парабола.

3) Приравнивая $y$ к $0$ , мы узнаем точки пересечения параболы с осью (ох). Для этого решаем уравнение $ax^2+bx+c=0$ . В зависимости от дискриминанта, будем получать одну ( $D=0$ , $x=-\frac{b}{2a}$ ), две ( $D>0$ , $x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$ ) или нИсколько ( $D<0$ ) точек пересечения с осью (ох). В предыдущем примере у нас корень из дискриминанта – не целое число, при построении нам особо нет смысла находить корни, но мы видим четко, что две точки пересечения с осью (ох) у нас будут (так как $D>0$ ), хотя, в общем, это видно и без дискриминанта.

Итак, давайте выработаем

Алгоритм для построения параболы, если она задана в виде $y=ax^2+bx+c$

1) определяем направление ветвей ( а>0 – вверх, a<0 – вниз)

2) находим координаты вершины $(x_o;y_o)$ параболы по формуле $x_o=\frac{-b}{2a}$ , $y_o=y(x_o)$ .

3) находим точку пересечения параболы с осью (оу) по свободному члену $c$ , строим точку, симметричную данной относительно оси симметрии параболы (надо заметить, бывает, что эту точку невыгодно отмечать, например, потому, что значение $c$ велико… пропускаем этот пункт…)

4) В найденной точке – вершине параболы (как в точке (0;0) новой системы координат) строим параболу $y=ax^2$ . Если $|a|>1$ , то парабола $y=ax^2$ становится у’же по сравнению с $y=x^2$ , если $|a|<1$ , то парабола расширяется по сравнению с $y=x^2$

5) Находим точки пересечения параболы с осью (оу) (если они еще сами “не всплыли”), решая уравнение $ax^2+bx+c=0$

Пример 1

алгоритм построения параболы, парабола

Пример 2

парабола, построение параболы, ветви параболы, коэффициенты параболы, дискриминант

Замечание 1. Если же парабола изначально нам задана в виде $y=a(x-m)^2+n$ , где $m, n$ – некоторые числа (например, $y=(x-5)^2-1$ ), то построить ее будет еще легче, потому что нам уже заданы координаты вершины $(m, n)$ . Почему?

Возьмем квадратный трехчлен $ax^2+bx+c$ и выделим в нем полный квадрат: $ax^2+bx+c=a(x^2+\frac{b}{a}x+\frac{c}{a})=a((x^2+2\frac{b}{2a}x+\frac{b^2}{4a^2})-\frac{b^2}{4a^2}+\frac{c}{a})=a(x+\frac{b}{2a})^2-\frac{b^2}{4a}+c.$ Посмотрите, вот мы и получили, что $m=\frac{-b}{2a}$ , $n=-\frac{b^2}{4a}+c=y(\frac{-b}{2a})$ . Мы с вами ранее называли вершину параболы $(x_o; y_o)$ , то есть теперь $x_o=m$ , $y_o=n$ .

Например, $y=-\frac{1}{3}{(x+2)}^2+6$ . Отмечаем на плоскости вершину параболы $(-2; 6)$ , понимаем, что ветви направлены вниз, парабола расширена (относительно $y=x^2$ ). То есть выполняем пункты 1; 3; 4; 5 из алгоритма построения параболы (см. выше).

парабола с ветвями вниз

Замечание 2. Если парабола задана в виде, подобном этому $y=x(x-4)$ (то есть $y$ представлен в виде произведения двух линейных множителей), то нам сразу видны точки пересечения параболы с осью (ох). В данном случае – (0;0) и (4;0). В остальном же действуем согласно алгоритму, раскрыв скобки.

Автор: egeMax | комментариев 5 | Метки: графики функций, функции

Печать страницы

комментариев 5

Татьяна

2017-04-13 в 20:14

спасибо

[ Ответить ]
- egeMax
  
  2017-04-13 в 20:28
  
  [ Ответить ]
egeMax

2017-04-13 в 20:29

[ Ответить ]
Наталья

2021-09-09 в 13:19

У вас ошибка в замечании 1, неверно разложен трехчлен, и как следствие неверно расчитывается n. n=C-(b^2/4a)

[ Ответить ]
- egeMax
  
  2021-10-17 в 13:00
  
  Наталья, спасибо большое! Подправила
  
  [ Ответить ]