Если вы уже знакомы с тригонометрическим кругом, и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, тригонометрический круг:
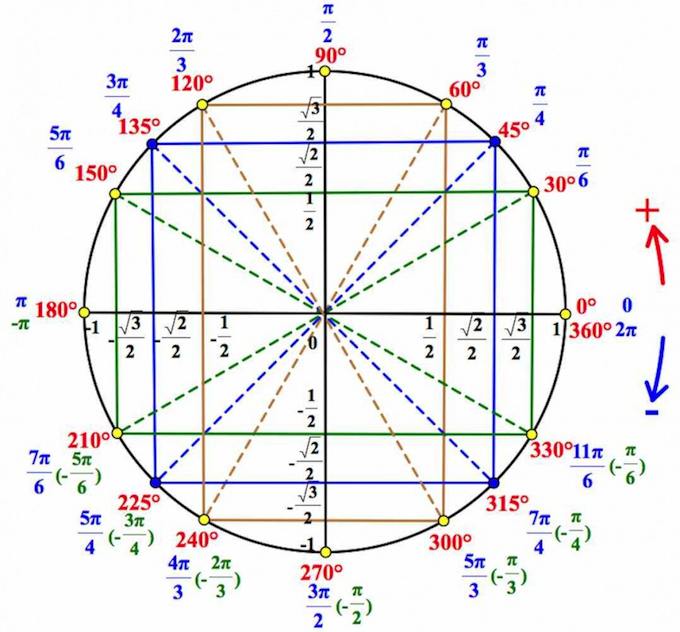
Мы же здесь будем все подробно разбирать шаг за шагом + показать
Тригонометрический круг – не роскошь, а необходимость
 Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Очень важно не махать рукой на значения тригонометрических функций, – мол, всегда можно посмотреть в шпору с таблицей значений.
Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!
Нас выручит тригонометрический круг! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!
К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул, чему равен синус, скажем, $300$ градусов, или $-45$.
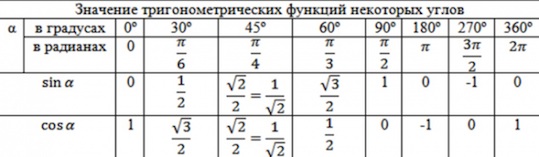
Никак?.. можно, конечно, подключить формулы приведения… А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!
А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.
Знакомство с тригонометрическим кругом
Давайте по порядку.
Сначала выпишем вот такой ряд чисел:
[latexpage]$\quicklatex{color=”#A9A9A9″}0,\;1,\;2,\;3,\;4$
А теперь такой:
$\sqrt0,\;\sqrt1,\;\sqrt2,\;\sqrt3,\;\sqrt4$
И, наконец, такой:
$\quicklatex{color=”#FF0000″}\frac{\sqrt0}{2},\;\frac{\sqrt1}{2},\;\frac{\sqrt2}{2},\;\frac{\sqrt3}{2},\;\frac{\sqrt4}{2}$
Конечно, понятно, что, на самом-то деле, на первом месте стоит $0$, на втором месте стоит $\frac{1}{2}$, а на последнем – $1$. То есть нас будет больше интересовать цепочка $\quicklatex{color=”#FF0000″}0,\;\frac{1}{2},\;\frac{\sqrt2}{2},\;\frac{\sqrt3}{2},\;1$.
Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».
И зачем оно нам?
Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.
Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).
От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы $30^{\circ},\;45^{\circ},\;60^{\circ},\;90^{\circ}$.
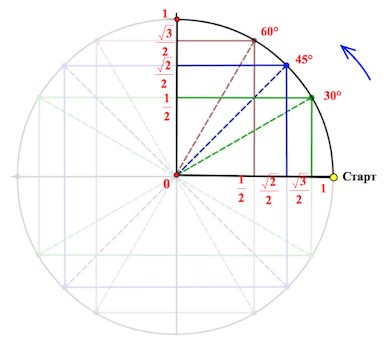 Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.
Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.
Это почему же, спросите вы?
Не будем разбирать все. Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.
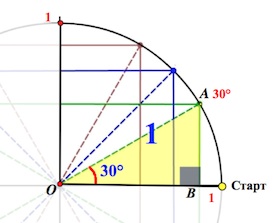
Треугольник АОВ – прямоугольный, в нем $\angle O=30^{\circ}$. А мы знаем, что против угла в $30^{\circ}$ лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть $1$).
Значит, АВ=$\frac{1}{2}$ (а следовательно, и ОМ=$\frac{1}{2}$). А по теореме Пифагора $OB=\frac{\sqrt3}{2}.$
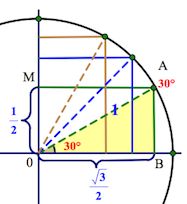
Надеюсь, уже что-то становится понятно?
Наконец, что такое синус, косинус в прямоугольном треугольнике?
$\sin\angle AOB=\frac{AB}{OA}=\frac{\frac{1}{2}}{1}=\frac{1}{2},$
$\cos\angle AOB=\frac{OB}{OA}=\frac{\frac{\sqrt3}{2}}{1}=\frac{\sqrt3}{2}.$
Так вот точка В и будет соответствовать значению $\cos 30^{\circ}$, а точка М – значению $\sin 30^{\circ}.$
Аналогично с остальными значениями первой четверти.
Как вы понимаете, привычная нам ось (ox) будет осью косинусов, а ось (oy) – осью синусов. Про тангенс и котангенс позже.
Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.
Итак, вот он, ВСЕМОГУЩИЙ тригонометрический круг, без которого никуда в тригонометрии.

А вот как пользоваться тригонометрическим кругом, мы поговорим в следующей статье.


Спасибо огромное! именно эту инфу два часа найти не мог=)
спасибо понятно ничего не понятно
Отличная статья! Даже при минимуме знаний все становится абсолютно понятно. Автору большое спасибо))))
супер! очень умело
сасибо, за труд!
Ничего лучше по этой теме не читала. Спасибо большое!
спасибо,все понятно даже родителям.
Спасибо, быстро и понятно.