Часть 1
(Часть 2 см. здесь)
Примеры решения простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами называются неравенства вида
$sinx\vee a$,
$cosx\vee a$,
$tgx\vee a$,
$ctgx\vee a$,
где $\vee$ – один из знаков $<,\;>,\;\leq,\;\geq$, $a\in R$.
Вы должны прежде, конечно, хорошо ориентироваться в тригонометрическом круге и уметь решать простейшие тригонометрические уравнения (часть I, часть II).
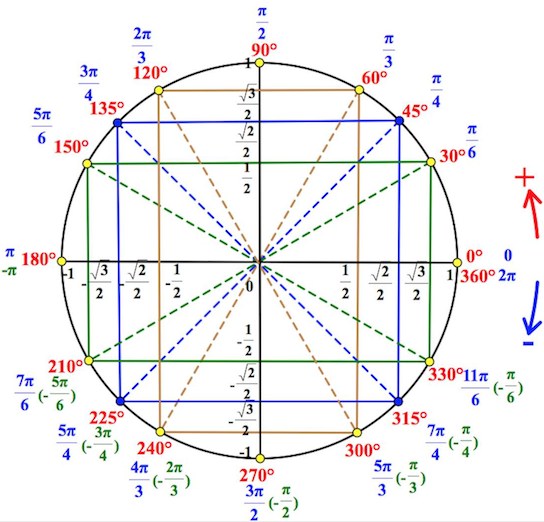
Кстати, умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.
Сначала мы рассмотрим простейшие тригонометрические неравенства с синусом и косинусом. Во второй части статьи – с тангенсом, котангенсом.
Пример 1
Решить неравенство: $cosx<\frac{1}{2}.$
Решение: + показать
Отмечаем на оси косинусов $\frac{1}{2}.$
Все значения $cosx$, меньшие $\frac{1}{2},$ – левее точки $\frac{1}{2}$ на оси косинусов.
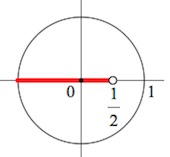
Отмечаем все точки (дугу, точнее – серию дуг) тригонометрического круга, косинус которых будет меньше $\frac{1}{2}.$
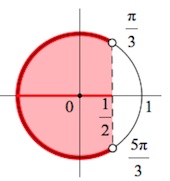
Полученную дугу мы проходим против часовой стрелки (!), то есть от точки $\frac{\pi}{3}$ до $\frac{5\pi}{3}$.
Обратите внимание, многие, назвав первую точку $\frac{\pi}{3},$ вместо второй точки $\frac{5\pi}{3}$ указывают точку $-\frac{\pi}{3}$, что неверно!
Становится видно, что неравенству удовлетворяют следующие значения $x:$
$\frac{\pi}{3}+2\pi n<x<\frac{5\pi}{3}+2\pi n,\;n\in Z.$
Следите за тем, чтобы «правая/вторая точка» была бы больше «левой/первой».
Не забываем «накидывать» счетчик $2\pi n,\;n\in Z.$
Вот так выглядит графическое решение неравенства не на тригонометрическом круге, а в прямоугольной системе координат:
Пример 2
Решить неравенство: $cosx\geq -\frac{\sqrt2}{2}.$
Решение: + показать
Отмечаем на оси косинусов $-\frac{\sqrt2}{2}.$
Все значения $cosx$, большие или равные $-\frac{\sqrt2}{2}$ – правее точки $-\frac{\sqrt2}{2}$, включая саму точку.
Тогда выделенные красной дугой аргументы $x$ отвечают тому условию, что $cosx\geq -\frac{\sqrt2}{2}$.
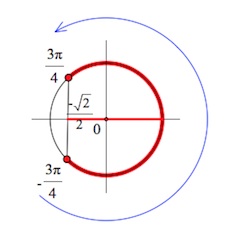$-\frac{3\pi}{4}+2\pi n\leq x\leq \frac{3\pi}{4}+2\pi n,\; n\in Z.$
Пример 3
Решить неравенство: $sinx\geq -\frac{\sqrt3}{2}.$
Решение:+ показать
Отмечаем на оси синусов $-\frac{\sqrt3}{2}.$
Все значения $sinx$, большие или равные $-\frac{\sqrt3}{2},$ – выше точки $-\frac{\sqrt3}{2}$, включая саму точку.
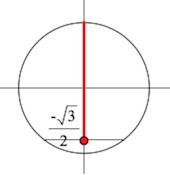
«Транслируем» выделенные точки на тригонометрический круг:
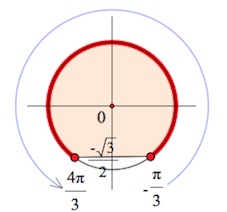$-\frac{\pi}{3}+2\pi n \leq x\leq \frac{4\pi}{3}+2\pi n,\;n\in Z$
Пример 4
Решить неравенство: $sinx<1.$
Решение:+ показать
Кратко:
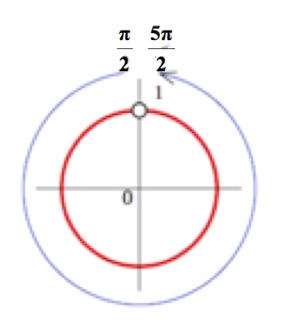
$\frac{\pi}{2}+2\pi n<x<\frac{5\pi}{2}+2\pi n,\;n\in Z$
или все $x$, кроме $\frac{\pi}{2}+2\pi n,\;n\in Z.$
Пример 5
Решить неравенство: $sinx\geq 1.$
Решение:+ показать
Неравенство $sinx\geq 1$ равносильно уравнению $sinx=1$, так как область значений функции $y=sinx$ – $[-1;1].$
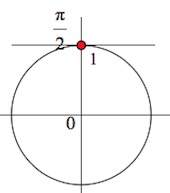
$x=\frac{\pi}{2}+2\pi n,\;n\in Z.$
Пример 6
Решить неравенство: $sinx<\frac{1}{3}.$
Решение:+ показать
Действия – аналогичны применяемым в примерах выше. Но дело мы имеем не с табличным значением синуса.
Здесь, конечно, нужно знать определение арксинуса.
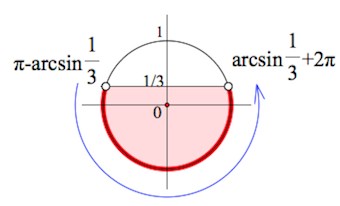
$\pi -arcsin\frac{1}{3}+2\pi n<x<arcsin\frac{1}{3}+2\pi+2\pi n,\;n\in Z$
Если не очень понятно, загляните сюда –>[spoiler]
Согласны с таким вариантом (одним из) названия углов, соответствующих тому, что синус в них равен $\frac{1}{3},\;-\frac{1}{3}?$
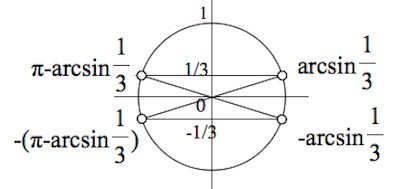
А теперь мы должны позаботиться о том, чтобы правый конец промежутка, являющего собой решение неравенства, был бы больше левого конца.
Поэтому
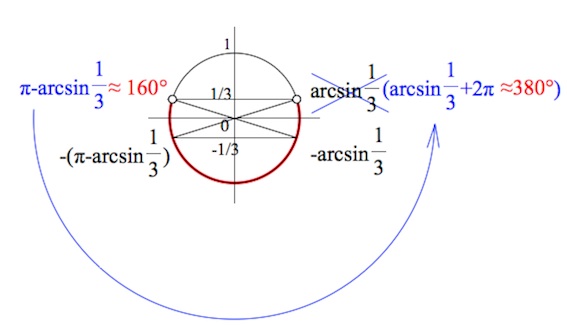
Тренируемся в решении простейших тригонометрических неравенств
Имейте ввиду, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. Например, в задании 2 ответ можно было записать и так: $\frac{5\pi}{4}+2\pi n\leq x\leq \frac{11\pi}{4}+2\pi n,\; n\in Z.$
1. Решить неравенство: $sinx<-\frac{1}{2}.$
Ответ: + показать
$(-\frac{5\pi}{6}+2\pi n;-\frac{\pi}{6}+2\pi n),\;n\in Z$
2. Решить неравенство: $cosx>-\frac{1}{2}.$
Ответ: + показать
$(-\frac{2\pi}{3}+2\pi n;\frac{2\pi}{3}+2\pi n),\;n\in Z$
3. Решить неравенство: $sinx\geq -1.$
Ответ: + показать
$(-\infty;+\infty)$
4. Решить неравенство: $sinx\geq 0.$
Ответ: + показать
$[2\pi n;\pi +2\pi n,\;n\in Z]$
5. Решить неравенство: $cosx\leq 0,2.$
Ответ: + показать
$[arccos0,2+2\pi n;2\pi-arccos0,2+2\pi n,\;n\in Z]$
Часть 2
Если у вас есть вопросы, – пожалуйста, – спрашивайте!
Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
Помогите решить пожалуйста:
sin x≥-√2
Неравенство верно при всех x.
Ясно,спасибо
Здравствуйте можете помочь решить их 10cos^2x+3cosx-1≥0 и
6sin^2x-sinx-1≤0
10(2cos^2x-1)+3cosx-1>=0;
20cos^2x+3cosx-11>=0;
А дальше дискриминант кривой. Верно условие-то переписано?
10cos2(тут 2 квадрат)x+3 cosx-1≥0
Аа…
10cos^2x+3cosx-1>=0;
10(cosx+0,5)(cosx-0,2)>=0;
Cosx<=-0,5 или cosx>=0,2;
X in [2pi/3+2pin;4pi/3+2pin] или x in [-arccos0,2+2pin;arccos0,2+2pin], n in Z.
Второе неравенство – аналогично.
спасибо
Помогите пожалуйста, срочно
Cos(5x+п/4)>0
-п/2+2пn<5х+п/4<п/2+2пn, n in Z Ну и далее...
Хотелось бы еще примеры на функцию тангес
CosX1.1
2CosX+√2≥2
Помогите пожалуйста
Огромное спасибо за понятное объяснение! Подскажите пожалуйста почему чтобы определить точки на единичной окружности иногда от пи а иногда от 2пи отнимаем значение угла x например. x=arcsin (a) Cпасибо!
Помогите пожалуйста решить sin x^0??
Sin 1 ???
Помогите пожалуйста решить 2sin^2x-7sinx+3>(больше или равно) 0
ctg2.8<0 sin2.80 tg2.8>0 sin 208>1 помогите с обяснением плиз
ничего не понял