Элементы треугольника. Медиана

Елена Репина 2013-04-15 2013-07-31

Определение

Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны

медиана треугольника, свойства медианы треугольника

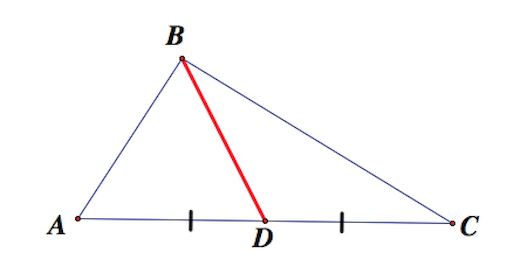
Свойства

1. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.

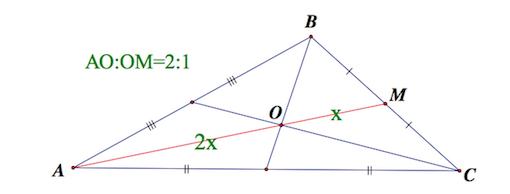
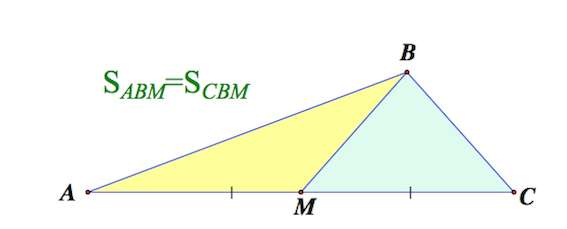
медиана треугольника, свойства медианы треугольника

2. Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника)

медиана треугольника, свойства медианы треугольника

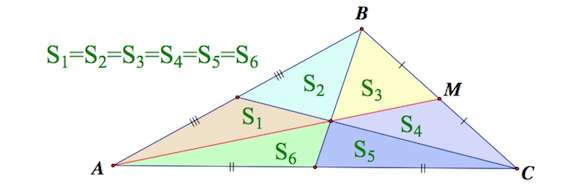
3. Медианы треугольника делят треугольник на 6 равновеликих треугольников

медиана треугольника, свойства медианы треугольника, равновеликие треугольники

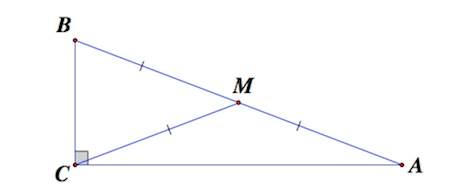
4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы

медиана треугольника, свойства медианы треугольника, медиана в прямоугольном треугольнике

5. Длина медианы треугольника вычисляется по формуле:

$m_c =\frac {\sqrt{2a^2+2b^2-c^2}}{2}$ , где где $m_c$ — медиана к стороне $c$ ; $a,\;b,\;c$ — стороны треугольника

6. Длина стороны треугольника через медианы вычисляется по формуле:

$a=\frac{2}{3}\sqrt {2 (m_b^2 + m_c^2) - m_a^2}$ , где $m_a, m_b, m_c$ – медианы к соответствующим сторонам треугольника, $a, b, c$ — стороны треугольника.

Автор: egeMax | Нет комментариев

Печать страницы

Элементы треугольника. Медиана

Определение

Свойства

Добавить комментарий Отменить ответ