Графики тригонометрических функций. Тангенс, котангенс

График функции y=tgx

Если вы умеете работать с тригонометрическим кругом, то вам не составит труда построить график функции $y=tgx$.

Надеюсь, вы помните, где располагается ось тангенсов…

Глядя на картинку, хорошо видно, что значения тангенса в I и III четвертях совпадают с соответствующими значениями тангенса II и IV  четвертей. (Например, $tg150^{\circ}=tg(330^{\circ})=-\frac{1}{\sqrt3},\;tg225^{\circ}=tg45^{\circ}=1$ и т.д.)

Переносим  основные значения углов, представленные на круге, например, из I и IV четвертей и соответствующие им значения тангенса на координатную плоскость.

По оси абсцисс откладываем угол в радианах, по оси ординат — значения тангенса угла.

Нанесенные на координатную плоскость точки подсказывают нам плавную кривую.  Это и есть график функции $y=tgx$ на $(-\frac{\pi}{2};\frac{\pi}{2})$.

Обратите внимание! Тангенс в точках $-\frac{\pi}{2},\;\frac{\pi}{2}$ не существует. Мы лишь можем сколь угодно близко «подбираться» к этим значениям.

Указанный выше фрагмент графика тангенса будет для нас являться как бы штампом. Тиражируя этот фрагмент, мы и получим вот такой график функции $y=tgx$:

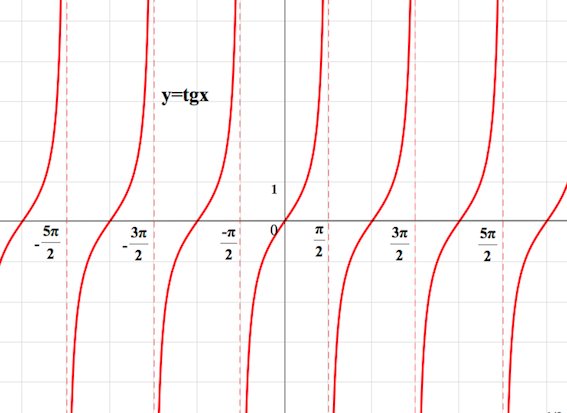
График функции является симметричным относительно начала координат.

 График функции y=ctgx

Точно также, как мы строили график $y=tgx$ при помощи тригонометрического круга, мы могли бы построить и $y=ctgx$.

Поступим несколько иначе.

Согласно формулам приведения $tg(\frac{\pi}{2}+x)=-ctgx$ или, что тоже самое, что $-tg(\frac{\pi}{2}+x)=ctgx$.

Из чего мы делаем вывод, что график функции $y=ctgx$ будет получен смещением графика функции $y=tgx$ на  $\frac{\pi}{2}$ единиц влево и при этом график $y=tg(\frac{\pi}{2}+x)$ «опрокидывается» относительно оси (ox) за счет коэффициента -1.

График функции является симметричным относительно начала координат.