Способы решения систем уравнений с двумя неизвестными

• Выражаем одну переменную через другую.

• Выраженную из одного уравнения переменную подставляем во второе уравнение. Получаем уравнение относительно одной переменной, которое и решаем.

• Опираясь на найденное значение одной переменной, находим значение второй, подставляя в оставшееся уравнение.

Из первого уравнения системы выражаем $y$ через $x$ и подставляем во второе уравнение:

$\begin{cases}y=3x-2,\\3x+5(3x-2)=8;&\end{cases}$

Вторая строка системы – уравнение с одной переменной. Решаем его и найденное значение $x$ подставляем в первое уравнение для нахождения $y$.

$\begin{cases}y=1,\\x=1;&\end{cases}$

Ответ: $(1;1).$

• Добиваемся, путем равносильных преобразований, наличия равных (или противоположных) коэффициентов при одной из неизвестных переменных в уравнениях.

• Вычитаем (или складываем) полученные уравнения с целью выхода на уравнение с одной неизвестной.

• Решаем  полученное уравнение с одной неизвестной.

• Найденное значение одной переменной подставляем в любое из уравнений системы, находим значение второй.

Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.

$\begin{cases}6y=6,\\3x+5y=8;&\end{cases}$

$\begin{cases}y=1,\\3x+5\cdot 1=8;&\end{cases}$

$\begin{cases}y=1,\\x=1;&\end{cases}$

Ответ: $(1;1).$ 

Прежде домножаем первую строку системы $3$, вторую строку системы – на $4$. Вычитаем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.

$\begin{cases}12x-6y=3,\\12x-12y=-8;&\end{cases}$

$\begin{cases}6y=11,\\3x-3\cdot \frac{11}{6}=-2;&\end{cases}$

$\begin{cases}y=\frac{11}{6},\\x=\frac{7}{6};&\end{cases}$

Ответ: $(\frac{7}{6};\frac{11}{6}).$ 

Можно сделать замену $\frac{1}{x}=t$ и $\frac{1}{y}=m.$ Тогда выходим на систему линейных уравнений:

$\begin{cases}3t-4m=1,\\2t+5m=4,5;&\end{cases}$

Систему можно решить методом сложения, например.

Но приведем решение без замены.

Умножим первое уравнение системы на $5$, второе – на $4$ и произведем сложение полученных уравнений, оставим при этом в системе, например, первое уравнение исходной системы.

$\begin{cases}\frac{15}{x}-\frac{20}{y}=5,\\\frac{8}{x}+\frac{20}{y}=18;&\end{cases}$

$\begin{cases}\frac{23}{x}=23,\\\frac{3}{x}-\frac{4}{y}=1;&\end{cases}$

$\begin{cases}x=1,\\\frac{3}{1}-\frac{4}{y}=1;&\end{cases}$

$\begin{cases}x=1,\\\frac{4}{y}=2;&\end{cases}$

$\begin{cases}x=1,\\y=2;&\end{cases}$

Ответ: $(1;2).$ 

Можно сделать замену $|x|=t$ и выйти на систему линейных уравнений:

$\begin{cases}3t+2y=1,\\2t-y=3;&\end{cases}$

Приведем решение без замены.

Выражаем $y$ из второго уравнения системы и подставляем в первое.

$\begin{cases}3|x|+2(2|x|-3)=1,\\y=2|x|-3;&\end{cases}$

$\begin{cases}7|x|=7,\\y=2|x|-3;&\end{cases}$

$\begin{cases}x=\pm 1,\\y=2\cdot 1-3;&\end{cases}$

$\begin{cases}x=\pm 1,\\y=-1;&\end{cases}$

Ответ: $(1;-1), (-1;-1).$ 

Выражаем $y+1$ из первого уравнения системы и подставляем во второе.

$\begin{cases}y+1=\frac{16}{x},\\\frac{x}{\frac{16}{x}}=4;&\end{cases}$

$\begin{cases}y+1=\frac{16}{x},\\x^2=64;&\end{cases}$

$\begin{cases}y=\frac{16}{x}-1,\\x=\pm 8;&\end{cases}$

$\left[\begin{array}{rcl}\begin{cases}x=8,\\y=1;\end{cases}\\\begin{cases}x=-8,\\y=-3;\end{cases}\end{array}\right.$

Ответ: $(8;1), (-8;-3).$ 

Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.

$\begin{cases}2x=6xy,\\x-y=xy;&\end{cases}$

$\begin{cases}x=3xy,\\x-y=xy;&\end{cases}$

$\begin{cases}x(1-3y)=0,\\x-y=xy;&\end{cases}$

$\left[\begin{array}{rcl}\begin{cases}x=0,\\y=0;\end{cases}\\\begin{cases}y=\frac{1}{3},\\x=\frac{1}{2};\end{cases}\end{array}\right.$

Ответ: $(0;0),(\frac{1}{2};\frac{1}{3}).$ 

$\begin{cases}x(1+y^3)=9,\\xy(1+y)=6;&\end{cases}$

Производим деление первой строки на вторую, оставляем в системе вторую строку без изменений (заметили, что $x\neq 0, y\neq 0).$

$\begin{cases}\frac{1+y^3}{y(1+y)}=\frac{3}{2},\\xy(1+y)=6;&\end{cases}$

$\begin{cases}\frac{(1+y)(1-y+y^2)}{y(1+y)}=\frac{3}{2},\\xy(1+y)=6;&\end{cases}$

$\begin{cases}\frac{1-y+y^2}{y}=\frac{3}{2},\\xy(1+y)=6;&\end{cases}$

$\begin{cases}2y^2-5y+2=0,\\xy(1+y)=6;&\end{cases}$

$\left[\begin{array}{rcl}\begin{cases}y=2,\\x=1;\end{cases}\\\begin{cases}y=\frac{1}{2},\\x=8;\end{cases}\end{array}\right.$

Ответ: $(1;2),(8;0,5).$ 

$\begin{cases}xy-29=x+y,\\(x+y)^2-2xy=x+y+72;&\end{cases}$

При замене $x+y=u, xy=v$  приходим к следующей системе

$\begin{cases}v-29=u,\\u^2-2v=u+72;&\end{cases}$

 которую будем решать способом подстановки:

$\begin{cases}v-29=u,\\(v-29)^2-2v=v-29+72;&\end{cases}$

$\begin{cases}u=v-29,\\v^2-61v+798=0;&\end{cases}$

$\left[\begin{array}{rcl}\begin{cases}v=42,\\u=13;\end{cases}\\\begin{cases}v=19,\\u=-10;\end{cases}\end{array}\right.$

Производим обратную замену:

$\left[\begin{array}{rcl}\begin{cases}xy=42,\\x+y=13;\end{cases}\\\begin{cases}xy=19,\\x+y=-10;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}x^2-13x+42=0,\\y=13-x;\end{cases}\\\begin{cases}x^2+10x+19=0,\\y=-10-x;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}x=7,\\y=6;\end{cases}\\\begin{cases}x=6,\\y=7;\end{cases}\\\begin{cases}x=-5+\sqrt6,\\y=-5-\sqrt6;\end{cases}\\\begin{cases}x=-5-\sqrt6,\\y=-5+\sqrt6;\end{cases}\end{array}\right.$

Ответ: $(7;6),(6;7),(-5+\sqrt6;-5-\sqrt6),(-5-\sqrt6;-5+\sqrt6).$

Первое уравнение системы – однородное. Производим деление первого уравнения системы на $x^2$ (можно и на $y^2$ или $xy$). Заметим, опасности деления на ноль нет.

$\begin{cases}1+3(\frac{y}{x})+2(\frac{y}{x})^2=0,\\x^2+y^2=20;&\end{cases}$

Первое уравнение системы – квадратное относительно $\frac{y}{x}$.

$\left[\begin{array}{rcl}\begin{cases}\frac{y}{x}=-1,\\x^2+y^2=20;\end{cases}\\\begin{cases}\frac{y}{x}=-\frac{1}{2},\\x^2+y^2=20;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}y=-x,\\x^2+y^2=20;\end{cases}\\\begin{cases}x=-2y,\\4y^2+y^2=20;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}y=-x,\\x=\pm \sqrt{10};\end{cases}\\\begin{cases}x=-2y,\\y=\pm 2;\end{cases}\end{array}\right.$

Ответ: $(\sqrt{10},-\sqrt{10}),(-\sqrt{10};\sqrt{10}), (2;-4),(-2;4).$

Применим прежде к системе метод сложения. После чего выйдем на однородное уравнение.

$\begin{cases}x^2+3xy+2y^2=0,\\3xy+7y^2=1;&\end{cases}$

$\begin{cases}1+3(\frac{y}{x})+2(\frac{y}{x})^2=0,\\3xy+7y^2=1;&\end{cases}$

$\left[\begin{array}{rcl}\begin{cases}\frac{y}{x}=-1,\\3xy+7y^2=1;\end{cases}\\\begin{cases}\frac{y}{x}=-\frac{1}{2},\\3xy+7y^2=1;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}\frac{y}{x}=-1,\\-3x^2+7y^2=1;\end{cases}\\\begin{cases}\frac{y}{x}=-\frac{1}{2},\\-6y^2+7y^2=1;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}y=-x,\\y=\pm 0,5;\end{cases}\\\begin{cases}x=-2y,\\y=\pm 1;\end{cases}\end{array}\right.$

Ответ: $(-0,5;0,5),(0,5;-0,5),(1;-2),(-1;2).$

Выразим в обеих строках системы $y$ через $x$:

$\begin{cases}y=5-x,\\y=\frac{4}{x};&\end{cases}$

Первое уравнение системы задает прямую, второе – гиперболу. Строим графики в одной системе координат, находим координаты точек пересечения графиков.

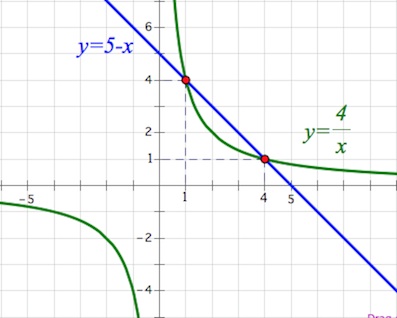
Ответ: $(1;4),(4;1).$

Первая строка системы задает окружность с центром в точке $(3;2)$ радиусом $1$.  Вторая строка системы задает прямую $y=x-2$.

Находим координаты точек пересечения графиков: $(3;1), (4;2).$

Ответ: $(3;1), (4;2).$

Первая строка системы задает параболу с ветвями вверх с вершиной в точке $(1;0)$.

Так как $x^2+6x+5=(x+1)(x+5)$, то из второй строки системы$y=x+5$ при условии, что $x\neq -1.$ То есть вторая строка системы задает прямую с выколотой точкой $(-1;4).$

Ответ: $(4;9)$

Решите системы уравнений:

1. $\begin{cases}x+y=3\\-x+7y=13;&\end{cases}$

Ответ: $(1;2).$

2. $\begin{cases}\frac{6}{x+y}+\frac{5}{x-y}=7,\\\frac{3}{x+y}-\frac{2}{x-y}=-1;&\end{cases}$

Ответ: $(2;1).$

3. $\begin{cases}3|x|+2y=1,\\2|x|-y=3;&\end{cases}$

Ответ: $(1;-1),(-1;-1).$

4. $\begin{cases}\frac{x-1}{y+2}=2,\\(x-1)^2+(y+2)^2=45;&\end{cases}$

Ответ: $(7;1),(-5;-5).$

5. $\begin{cases}7-x+y-xy=0,\\5-y+x-xy=0;&\end{cases}$

Ответ: $(3;2),(-2;-3).$

6. $\begin{cases}xy^2-x=9,\\xy-xy^3=-18;&\end{cases}$

Ответ: $(3;2).$

7. $\begin{cases}xy+2x+2y=5,\\x^2+y^2+3x+3y=8;&\end{cases}$

Ответ: $(1;1).$

8. $\begin{cases}2x^2-2xy+3y^2=3,\\x^2-xy+2y^2=2;&\end{cases}$

Ответ: $(0;1),(0;-1),(1;1),(-1;-1).$

Решите графически системы уравнений:

9. $\begin{cases}y=|x^2+6x+5|,\\y-x=5;&\end{cases}$

Ответ: $(-5;0),(-2;3),(0;5).$

10. $\begin{cases}y=\frac{x^2-4x-12}{x+2},\\y=\frac{8}{x+1};&\end{cases}$

Ответ: $(7;1).$