Решения отдельных заданий ЕГЭ по математике от 6 июня 2016 года
Задания вариантов можно найти здесь и здесь.
13.1.
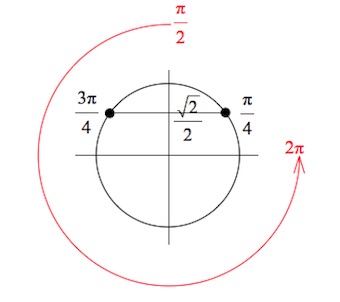
а) Решите уравнение: $2log_2^2(2sinx)-7log_2(2sinx)+3=0.$
б) Укажите корни этого уравнения, принадлежащие отрезку $[\frac{\pi}{2};2\pi].$
Решение: + показать
a)
$2log_2^2(2sinx)-7log_2(2sinx)+3=0.$
Перед нами квадратное уравнение относительно $log_2(2sinx).$
$2(log_2(2sinx)-3)(log_2(2sinx)-0,5)=0;$
$log_2(2sinx)=log_28$ или $log_2(2sinx)=log_2\sqrt2;$
$2sinx=8$ (решений нет) или $2sinx=\sqrt2;$
$sinx=\frac{\sqrt2}{2};$
$x=\frac{\pi}{4}+2\pi n,$ $x=\frac{3\pi}{4}+2\pi n, n\in Z.$
б) Корни уравнения, принадлежащие отрезку $[\frac{\pi}{2};2\pi]:$ $\frac{3\pi}{4}.$
Ответ:
а) $\frac{\pi}{4}+2\pi n,$ $\frac{3\pi}{4}+2\pi n, n\in Z;$
б) $\frac{3\pi}{4}.$
14.1. В правильной треугольной призме $ABCA_1B_1C_1$ сторона основания $AB$ равна $6$, а боковое ребро $AA_1$ равно $3$. На ребре $AB$ отмечена точка $K$ так, что $AK=1$. Точки $M$ и $L$ – середины ребер $A_1C_1$ и $B_1C_1$ соответственно. Плоскость $\alpha $ параллельна прямой $AC$ и содержит точки $K$ и $L$.
а) Докажите, что прямая $BM$ перпендикулярна плоскости $\alpha $.
б) Найдите расстояние от точки $C$ до плоскости $\alpha .$
Решение: + показать
a) Так как по условию $AC$ параллельна $\alpha,$ то по свойству прямой, параллельной плоскости, плоскость $ABC,$ содержащая $AC,$ пересекает $\alpha$ по прямой, параллельной $AC.$ Плоскость $\alpha$ имеет общую точку $K$ с плоскостью $(ABC)$, потому строим $KN:$ $N\in BC,KN\parallel AC$ ($CN=1$).
Плоскость $\alpha $ – это плоскость $(KLN).$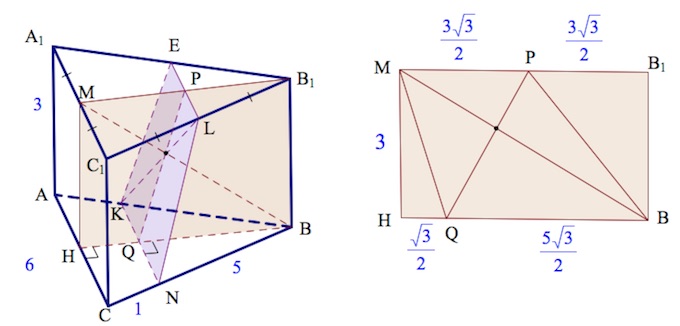
Пусть $H$ – проекция $M$ на $ABC$ ($H$ – середина $AC$).
По теореме о трех перпендикулярах, раз проекция $BH$ наклонной $MB$ на плоскость $ABC$ перпендикулярна $AC,$ то и сама наклонная $MB$ перпендикулярна $AC,$ а значит $MB$ перпендикулярна и $KN$ (по свойству параллельных прямых).
Докажем перпендикулярность $MB$ и $PQ,$ где $PQ$ – линия пересечения плоскостей $MHB,$ $\alpha$ (а именно, $P$ – середина $MB_1$, $Q$ – точка пересечения $HB,KN.$)
С одной стороны,
$S_{MPBQ}=S_{HMB_1B}-S_{MHQ}-S_{PB_1B}=9\sqrt3-\frac{3\sqrt3}{4}-\frac{9\sqrt3}{4}=6\sqrt3.$
С другой стороны,
$S_{MPBQ}=\frac{MB\cdot PQ\cdot sin \angle (MB;PQ)}{2}=\frac{6\cdot \sqrt{12}\cdot sin \angle (MB;PQ)}{2}=6\sqrt3\cdot sin \angle (MB;PQ).$
Стало быть, $sin \angle (MB;PQ)=1,$ что говорит о том, что $MB, PQ$ перпендикулярны.
Итак, прямая $MB$ перпендикулярна двум пересекающимся прямым ($PQ,KN$) плоскости $\alpha ,$ а значит, перпендикулярна плоскости $\alpha $ по признаку перпендикулярности прямой и плоскости.
б) Так как $AC\parallel \alpha ,$ то расстояние от точки $C$ до плоскости $\alpha $, – есть расстояние от $H$ до $\alpha $ ($H\in AC$).
Замечаем, что плоскости $HMB, \alpha $ перпендикулярны по признаку перпендикулярности плоскостей, ведь $MB$ перпендикулярна $\alpha .$
Тогда если в плоскости $MHB$ провести перпендикуляр $HF$ к $PQ,$ то по свойству перпендикулярных плоскостей $HF$ будет перпендикулярна $\alpha $.
Итак, искомое расстояние есть длина $HF$, где $HF\perp PQ.$
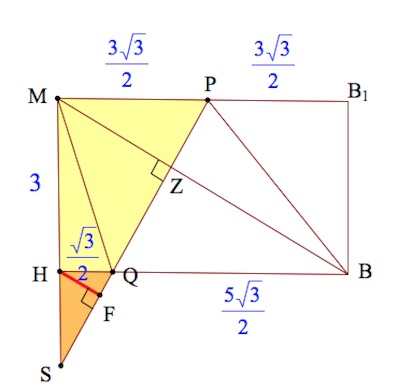
Пусть $MH$ пересекается с $PQ$ в точке $S.$
Треугольники $SMP, SHQ$ подобны, $k=3.$
Тогда $HF=\frac{MZ}{3},$ где $Z$ – точка пересечения $MB,PQ.$
Так как $MZ\cdot SP=MP\cdot MS,$ то $MZ=\frac{\frac{3\sqrt3}{2}\cdot \frac{9}{2}}{3\sqrt3}=\frac{9}{4}.$
Итак, $HF=\frac{MZ}{3}=\frac{3}{4}=0,75.$
Координатный способ решения части б).
Так как $AC\parallel \alpha ,$ то расстояние от точки $C$ до плоскости $\alpha $, – есть расстояние от $H$ до $\alpha $ ($H\in AC$).
Введем прямоугольную декартовую систему координат так, как показано на рисунке (центр – точка $H$, ось $x$ – луч $HC$, ось $y$ – луч $HB$, ось $z$ – луч $HM$).
Расстояние $\rho$ от точки $H$ до плоскости $KNL$ будем вычислять по формуле
$\rho=\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}}$
где $H(x_0;y_0;z_0)$, плоскость $KNL$ задается уравнением $Ax+By+Cz+D=0.$
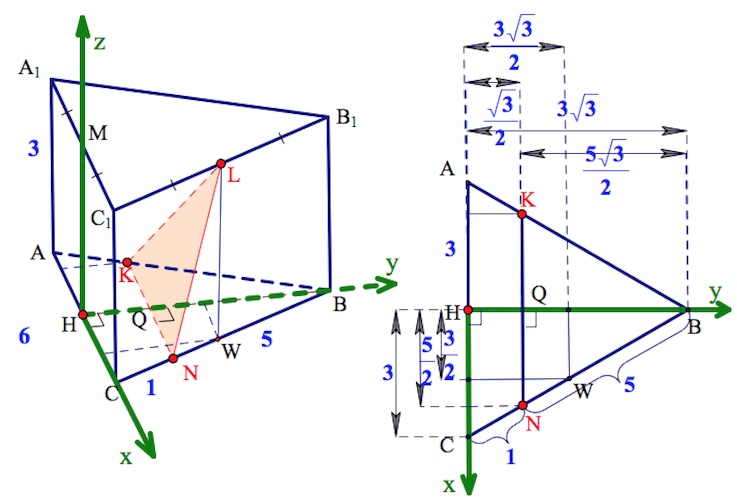
Не вдаваясь в подробности (см. рис.), перечислим координаты необходимых для вычисления точек:
$H(0;0;0),N(\frac{5}{2};\frac{\sqrt3}{2};0), K(-\frac{5}{2};\frac{\sqrt3}{2};0), L(\frac{3}{2};\frac{3\sqrt3}{2};3).$
Составим уравнение плоскости $KNL:$
$\begin{cases}a\cdot ({-\frac{5}{2}})+b\cdot \frac{\sqrt3}{2}+d=0,\\a\cdot ({\frac{5}{2}})+b\cdot \frac{\sqrt3}{2}+d=0,\\a\cdot ({\frac{3}{2}})+b\cdot \frac{3\sqrt3}{2}+3c+d=0;&\end{cases}$
$\begin{cases}a=0,\\b\cdot \frac{3\sqrt3}{2}+3c-b\cdot \frac{\sqrt3}{2}=0,\\a\cdot ({\frac{3}{2}})+b\cdot \frac{3\sqrt3}{2}+3c+d=0;&\end{cases}$
$\begin{cases}a=0,\\b=-\sqrt3c,\\d=-\frac{3c}{2};&\end{cases}$
Тогда уравнение плоскости $KNL$ примет вид
$-\sqrt3cy+cz-\frac{3c}{2}=0$
или
$-\sqrt3y+z-\frac{3}{2}=0$,
то есть
$A=0;B=-\sqrt3;C=1;D=-\frac{3}{2}.$
Итак, $\rho=\frac{|-\frac{3}{2}|}{\sqrt{3+1}}=0,75.$
Заметим, можно иначе обыграть задачу нахождения уравнения плоскости, если вспомнить, что коэффициенты $A,B,C$ из уравнения плоскости $Ax+By+Cz+D=0$ – это координаты вектора нормали плоскости. А в нашем случае $BM$ может выступать в качестве вектора нормали плоскости $KNL.$
Тогда, так как $\vec{BM}(0;3\sqrt3;-3),$ то, подставив в уравнение плоскости $Ax+By+Cz+D=0$ значения $A,B,C$ (то есть координаты вектора $BM$) и координаты, например, точки $N,$ получим:
$3\sqrt3\cdot \frac{\sqrt3}{2}+D=0,$ то есть $D=-4,5.$
Наконец, $\rho=\frac{|-4,5|}{\sqrt{27+3}}=0,75.$
Ответ: $0,75.$
15.1. Решите неравенство:
$\frac{25^x-5^{x+2}+26}{5^x-1}+\frac{25^x-7\cdot 5^{x}+1}{5^x-7}\leq 2\cdot 5^x-24.$
Решение: + показать
$\frac{25^x-25\cdot 5^{x}+26}{5^x-1}+\frac{25^x-7\cdot 5^{x}+1}{5^x-7}\leq 2\cdot 5^x-24;$
Готовимся к выделению целых частей дробей:
$\frac{(5^x-1)(5^x-24)+2}{5^x-1}+\frac{5^x(5^x-7)+1}{5^x-7}\leq 2\cdot 5^x-24;$
Выделяем целые части:
$5^x-24+\frac{2}{5^x-1}+5^x+\frac{1}{5^x-7}\leq 2\cdot 5^x-24;$
$\frac{2}{5^x-1}+\frac{1}{5^x-7}\leq 0;$
$\frac{2\cdot 5^x-14+5^x-1}{(5^x-1)(5^x-7)}\leq 0;$
$\frac{3\cdot 5^x-15}{(5^x-1)(5^x-7)}\leq 0;$
$\frac{5^x-5}{(5^x-1)(5^x-7)}\leq 0;$
Воспользуемся рационализацией:
$\frac{x-1}{x(x-log_57)}\leq 0;$
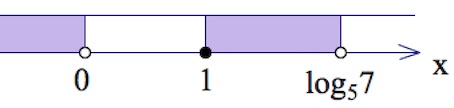
$x\in (-\infty;0)\cup [1;log_57).$
Ответ: $(-\infty;0)\cup [1;log_57).$
16.1. В трапеции $ABCD$ боковая сторона $AB$ перпендикулярна основаниям. Из точки $A$ на сторону $CD$ опустили перпендикуляр $AH$. На стороне $AB$ отмечена точка $E$ так, что прямые $CD$ и $CE$ перпендикулярны.
а) Докажите, что прямые $BH$ и $ED$ параллельны.
б) Найдите отношение $BH:ED,$ если угол $BCD$ равен $135^{\circ}.$
Решение: + показать
a)
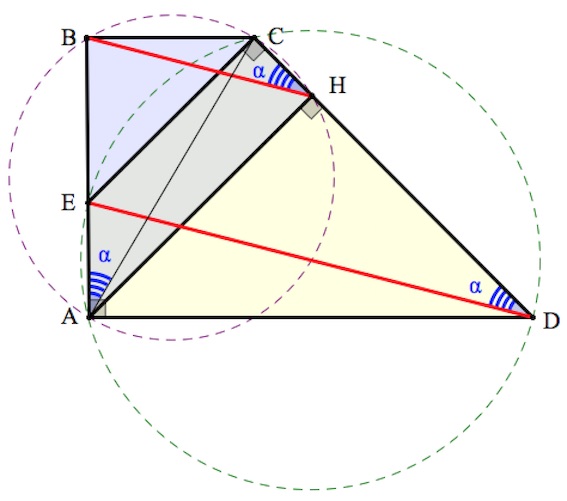
Около четырехугольника $AECD$ можно описать окружность, так как суммы противоположных углов равны ($\angle ECD=\angle BAD=90^{\circ}$).
Тогда углы $EDC,EAC$ равны как вписанные углы одной окружности, опирающиеся на одну дугу.
Около четырехугольника $ABCH$ можно описать окружность, так как суммы противоположных углов равны ($\angle ABC=\angle AHC=90^{\circ}$).
Тогда углы $EAC,BHC$ равны как вписанные углы одной окружности, опирающиеся на одну дугу.
Итак, $\angle BHC=\angle EDC.$ Указанные углы – соответственные углы при прямых $BH,ED$ и секущей $CD.$ Значит, по признаку параллельности прямых, $BH\parallel ED$. Что и требовалось доказать.
б) Пусть $AB$ пересекается с $DC$ в точке $P$.
Треугольники $PBH,PED$ подобны по двум углам, следовательно $BH:ED=PB:PE.$
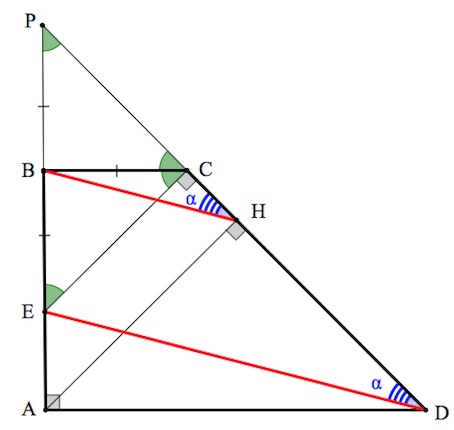
Очевидно, угол $P$ равен $45^{\circ}$. А так как $PCE$ прямой, то прямоугольный треугольник $PCE$ – равнобедренный. Очевидно, $CB$ – биссектриса в нем. Но тогда $CB$ также и медиана в треугольнике $PCE$. Стало быть, $BP=BE.$
Итак, $BH:ED=PB:PE=1:2.$
Ответ: б) $1:2.$
16.2. В треугольнике $ABC$ проведены высоты $AK$ и $CM$. На них из точек $M$ и $K$ опущены
перпендикуляры $ME,KH.$
а) Докажите, что прямые $EH$ и $AC$ параллельны.
б) Найдите отношение $EH:AC$, если угол $ABC$ равен $30^{\circ}.$
Решение: + показать
a) Треугольники $AMC, CKA$ имеют общую гипотенузу. Поэтому точки $A,M,K,C$ лежат на одной окружности. Тогда углы $ACM,AKM$ равны как вписанные углы, опирающиеся на одну дугу.
Аналогично треугольники $MEK, KHM$ имеют общую гипотенузу. Поэтому точки $E,M,H,K$ лежат на одной окружности. Тогда углы $MKE,MHE$ равны как вписанные углы, опирающиеся на одну дугу.
Итак, углы $MHE,ACM$ равны. Тогда по признаку параллельности прямых $EH,AC$ параллельны.

б) Пусть $AK,CM$ пересекаются в точке $O.$ В четырехугольнике $MBKO$ углы $M$ и $K$ в сумме дают $180^{\circ}.$ Тогда и углы $B,O$ в сумме дают $180^{\circ}.$ Угол $B$ по условию равен $30^{\circ}.$Тогда угол $O$ равен $150^{\circ}.$ Стало быть, угол $COK$ равен $30^{\circ}.$
$\Delta CHK:$
Пусть $HK=x,$ тогда $OK=2x$ и $OH=\sqrt3x.$
Очевидно, $\angle HKC=\angle COK=30^{\circ}.$
$\Delta HKC:$
Пусть $CH=y,$ тогда $CK=2y.$
Имеем:
$(2y)^2=y^2+x^2$, то есть $y=\frac{\sqrt3x}{3}.$

Из подобия треугольников $EOH,AOC$ имеем:
$\frac{EH}{AC}=\frac{OH}{OC}=\frac{\sqrt3x}{\sqrt3x+y}=\frac{\sqrt3x}{\sqrt3x+\frac{\sqrt3x}{3}}=\frac{3}{4}.$
Итак, $EH:AC=3:4$.
Ответ: б) $3:4.$
16.3. В трапеции $ABCD$ точка $E$ – середина основания $AD$, точка $M$ – середина боковой стороны $AB$. Отрезки $CE$ и $DM$ пересекаются в точке $O$.
а) Докажите, что площади четырёхугольника $AMOE$ и треугольника $COD$ равны.
б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника $AMOE$, если $BC=3,AD=4.$
Решение: + показать
а) Так как
$S_{AMOE}=S_{AMD}-S_{OED},$
$S_{OCD}=S_{ECD}-S_{OED},$
то достаточно доказать
$S_{AMD}=S_{ECD}.$

Пусть $h$ – высота трапеции, проведенная к $AD.$ Тогда расстояние от $M$ до $AD$ – есть $\frac{h}{2}.$
$S_{ECD}=\frac{1}{2}\cdot ED\cdot h.$
$S_{AMD}=\frac{1}{2}\cdot AD\cdot \frac{h}{2}=\frac{1}{2}\cdot 2ED\cdot \frac{h}{2}=\frac{1}{2}\cdot ED\cdot h=S_{ECD}.$
б) Площади треугольников $AOE,DOE$, как и площади треугольников $AOM,BOM$ равны (медиана делит треугольник на два равновеликих треугольника). Обозначим указанные площади как $n$ и $m$ соответственно.
Тогда $S_{OCD}=m+n.$

Пусть расстояние от точки $O$ до $AD$ – $h_1.$ Тогда расстояние от точки $O$ до $BC$ – $h-h_1.$
При этом
$n=\frac{1}{2}\cdot 2\cdot h_1=h_1.$
И
$m+2n=\frac{1}{2}\cdot h\cdot 2=h.$
Имеем:
$S_{BOC}=\frac{1}{2}\cdot 3\cdot (h-h_1)=\frac{3}{2}(m+n).$
Итак,
$\frac{S_{AMOE}}{S_{ABCD}}=\frac{m+n}{4,5(m+n)}=\frac{2}{9}.$
Ответ: б) $2:9.$
17.1. 15‐го января планируется взять кредит в банке на сумму $1$ млн рублей на $6$ месяцев. Условия его возврата таковы:
‐ 1‐го числа каждого месяца долг возрастает на целое число $r$ процентов по сравнению с концом предыдущего месяца;
‐ со 2‐го по 14‐е число каждого месяца необходимо выплатить часть долга;
‐ 15‐го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Найдите наименьшее значение $r$, при котором общая сумма выплат будет составлять более $1,25$ млн. рублей.
Решение: + показать
15.02. долг, после действия процентной ставки $r$, составит
$1+\frac{r}{100}$ млн. рублей.
Заемщик отдает банку
$\frac{1}{10}+\frac{r}{100}$ млн. рублей
и на счету остается
$\frac{9}{10}$ млн. рублей.
15.03. долг, после действия процентной ставки $r$, составит
$\frac{9}{10}+\frac{r}{100}\cdot \frac{9}{10}$ млн. рублей.
Заемщик отдает банку
$\frac{1}{10}+\frac{r}{100}\cdot \frac{9}{10}$ млн. рублей
и на счету остается
$\frac{8}{10}$ млн. рублей.
. . .
15.06. долг, после действия процентной ставки $r$, составит
$\frac{6}{10}+\frac{r}{100}\cdot \frac{6}{10}$ млн. рублей.
Заемщик отдает банку
$\frac{1}{10}+\frac{r}{100}\cdot \frac{6}{10}$ млн. рублей
и на счету остается
$\frac{5}{10}$ млн. рублей.
15.07. долг, после действия процентной ставки $r$, составит
$\frac{5}{10}+\frac{r}{100}\cdot \frac{5}{10}$ млн. рублей.
Заемщик отдает банку
$\frac{5}{10}+\frac{r}{100}\cdot \frac{5}{10}$ млн. рублей
и долг оказывается погашенным.
Итак, все выплаты заемщика составят
$5\cdot \frac{1}{10}+\frac{5}{10}+\frac{r}{100}(1+\frac{9}{10}+…+\frac{5}{10})=$
$=1+\frac{r}{1000}(10+9+8+7+6+5)=1+\frac{45r}{1000}.$
Так как, согласно условию, общая сумма выплат составляет более $1,25$ млн. рублей, составим неравенство:
$1+\frac{45r}{1000}>1,25;$
$\frac{45r}{1000}>0,25;$
$\frac{9r}{200}>\frac{1}{4};$
$r>\frac{50}{9};$
$r>5\frac{5}{9};$
Так как нас интересует наименьшее значение $r$ ($r$ – целое число по условию), то $r=6.$
Ответ: $6.$
18.1. Определите, при каких значениях параметра уравнение
$\sqrt{2^x-a}+\frac{a-2}{\sqrt{2^x-a}}=1$
имеет ровно два различных решения.
Решение: + показать
$\sqrt{2^x-a}+\frac{a-2}{\sqrt{2^x-a}}=1$
Обозначим за $\sqrt{2^x-a}$ за $m,$ заметив при этом, что $m>0.$ В силу возрастания функции $y=\sqrt{2^x-a},$ каждому конкретному положительному значению $m$ будет соответствовать единственное значение $x$.
Уравнение будет выглядеть так:
$m+\frac{a-2}{m}=1,m>0;$
или так:
$m^2-m+a-2=0,m>0$ (*)
Если уравнение имеет корни, то их сумма равна $1,$ а произведение равно $a-2$ (по теореме Виета).
Нам надо позаботится о том, чтобы оба корня уравнения (*) были бы положительными, чтобы исходное уравнение имело бы два различных корня. А это случится в случае положительного дискриминанта для (*) и положительности свободного члена уравнения (*).
Потому требуется решить систему неравенств:
$\begin{cases}1-4(a-2)>0,\\a-2>0;&\end{cases}$
$\begin{cases}a<\frac{9}{4},\\a>2;&\end{cases}$
Итак, $a\in (2;2,25).$
Ответ: $a\in (2;2,25).$
18.2. Определите, при каких значениях параметра уравнение
$\sqrt{15x^2+6ax+9}=x^2+ax+3$
имеет ровно три различных решения.
Решение: + показать
$\sqrt{15x^2+6ax+9}=x^2+ax+3;$
$15x^2+6ax+9=(x^2+ax+3)^2,x^2+ax+3\geq 0;$
Неплохо было бы выделить квадрат суммы или разности (относительно $x^2+ax+3$). Работаем в этом направлении.
$9x^2+6(x^2+ax+3)-9=(x^2+ax+3)^2,x^2+ax+3\geq 0;$
$9x^2=(x^2+ax+3)^2-6(x^2+ax+3)+9,x^2+ax+3\geq 0;$
В правой части равенства мы наблюдаем квадрат разности относительно $x^2+ax+3.$
$9x^2=((x^2+ax+3)-3)^2,x^2+ax+3\geq 0;$
$9x^2=(x^2+ax)^2,x^2+ax+3\geq 0;$
$(3x-(x^2+ax))(3x+(x^2+ax))=0,x^2+ax+3\geq 0;$
$x^2(3-x-a)(3+x+a)=0,x^2+ax+3\geq 0;$
Видим, что $x=0$ является корнем данного уравнения при любом значении $a$.
Чтобы уравнение имело бы три корня, остается потребовать, чтобы корни $x=0$, $x=3-a$, $x=-a-3$ были бы различны, при этом корни должны отвечать неравенству $x^2+ax+3\geq 0$.
Корни $x=3-a$, $x=-a-3$ не совпадают ни при каких значениях $a$. Корни $x=3-a$, $x=0$ совпадают при $a=3.$ Корни $x=-3-a$, $x=0$ совпадают при $a=-3.$
Осталось решить систему неравенств:
$\begin{cases}(3-a)^2+a(3-a)+3\geq 0,\\(-3-a)^2+a(-3-a)+3\geq 0;&\end{cases}$
$\begin{cases}a\leq 4,\\a\geq -4;&\end{cases}$
$a\in [-4;4].$
Итак, исходное уравнение будет иметь три различных корня при $a\in [-4;-3)\cup (-3;3)\cup (3;4].$
Ответ: $[-4;-3)\cup (-3;3)\cup (3;4].$
18.3. Определите, при каких значениях параметра уравнение
$\frac{x-2a}{x+2}+\frac{x-1}{x-a}=1$
имеет ровно один корень.
Решение: + показать
$\frac{x-2a}{x+2}+\frac{x-1}{x-a}=1;$
$\frac{(x-2a)(x-a)+(x-1)(x+2)-(x+2)(x-a)}{(x+2)(x-a)}=0;$
$x^2-(2a+1)x+2a^2+2a-2=0,$ $x\neq -2,$ $x\neq a;$
Рассмотрим дискриминант уравнения $x^2-(2a+1)x+2a^2+2a-2=0$:
$D=(2a+1)^2-4(2a^2+2a-2)=9-4a-4a^2.$
1) Если $9-4a-4a^2<0$, то есть $a\in (-\infty;-\frac{1+\sqrt{10}}{2})\cup (\frac{-1+\sqrt{10}}{2};+\infty),$ то уравнение не имеет корней.
2) Если $D=0,$ то есть $a=\frac{-1\pm \sqrt{10}}{2}$, мы должны быть уверены, что единственный корень уравнения $x^2-(2a+1)x+2a^2+2a-2=0$ (это $\frac{2a+1}{2}$) не окажется равным $-2$ и $a.$
А при $a=\frac{-1\pm \sqrt{10}}{2}$ это так.
3) Если $D>0,$ то есть $a\in (-\frac{1+\sqrt{10}}{2};\frac{-1+\sqrt{10}}{2}),$ то необходимо потребовать, чтобы один из корней был бы равен $-2,$ в то время как другой не равен $a$ или один из корней был бы равен $a,$ в то время как другой не равен $-2.$
Если один из корней $x_1$ уравнения $x^2-(2a+1)x+2a^2+2a-2=0$ – это $-2$, то второй корень $x_2$ можно найти по т. Виета:
$\begin{cases}-2\cdot x_2=2a^2+2a-2,\\-2+x_2=2a+1;&\end{cases}$
$\begin{cases}x_2=-a^2-a+1,\\x_2=2a+3;&\end{cases}$
$\begin{cases}a^2+3a+2=0,\\x_2=2a+3;&\end{cases}$
Если $a=-1$, то $x_2=1$ – не совпадает с $a.$
Если $a=-2$, то $x_2=-1$ – не совпадает с $a.$
При этом $a=-1$ и $a=-2$ входят в $(-\frac{1+\sqrt{10}}{2};\frac{-1+\sqrt{10}}{2}).$
То есть при $a=-1$, $a=-2$ исходное уравнение имеет один корень.
Если же один из корней $x_1$ уравнения $x^2-(2a+1)x+2a^2+2a-2=0$ – это $a$, то второй корень $x_2$ найдем из системы:
$\begin{cases}a\cdot x_2=2a^2+2a-2,\\a+x_2=2a+1;&\end{cases}$
$\begin{cases}a^2+a-2=0,\\x_2=a+1;&\end{cases}$
Если $a=1$, то $x_2=2$ – не совпадает с $-2.$
$a=-2$ – рассмотрено.
При этом $a=1$ входит в $(-\frac{1+\sqrt{10}}{2};\frac{-1+\sqrt{10}}{2}).$
То есть при $a=1$ исходное уравнение имеет один корень.
Итак, исходное уравнение имеет единственный корень при
$a\in ${$\frac{-1-\sqrt{10}}{2};-2;-1;1;\frac{-1+\sqrt{10}}{2}$}.
Ответ: {$\frac{-1-\sqrt{10}}{2};-2;-1;1;\frac{-1+\sqrt{10}}{2}$}.
18.4. Определите, при каких значениях параметра система уравнений
$\begin{cases}x(x^2+y^2+y-2)=|x|(y+2),\\y=x+a;&\end{cases}$
имеет ровно три различных решения.
Решение: + показать
$\left[\begin{array}{rcl}\begin{cases}x\geq 0,\\x(x^2+y^2+y-2)-x(y+2)=0;\end{cases}\\\begin{cases}x<0,\\x(x^2+y^2+y-2)+x(y+2)=0;\end{cases}\end{array}\right.$
$\left[\begin{array}{rcl}\begin{cases}x\geq 0,\\x(x^2+y^2+y-2-y-2)=0;\end{cases}\\\begin{cases}x<0,\\x(x^2+y^2+y-2+y+2)=0;\end{cases}\end{array}\right.$
$\left[\begin{array}{rcl}\begin{cases}x\geq 0,\\x(x^2+y^2-4)=0;\end{cases}\\\begin{cases}x<0,\\x(x^2+y^2+2y)=0;\end{cases}\end{array}\right.$
Первая строка исходной системы задает объединение двух полуокружностей ($x^2+(y+1)^2=1, x<0$ и $x^2+y^2=4, x>0$) и прямой $x=0.$

Вторая строка исходной системы – семейство параллельных прямых, проходящих под углом $45^{\circ}$ к оси $ox.$
1) Очевидно, $a$, отвечающее за прохождение прямой $y=x+a$ через точку $(0;-2)$ – это $-2.$
2) Очевидно, $a$, отвечающее за прохождение прямой $y=x+a$ через точку $(0;0)$ – это $0.$
3) $a$, отвечающее за касание прямой $y=x+a$ и большой полуокружности находим из условия:
$D=0$ для $x^2+(x+a)^2=4.$
$D$ для $2x^2+2ax+a^2-4=0$ – есть $-a^2+8,$
поэтому требуем: $8-a^2=0.$
Из двух вариантов $a=\pm 2\sqrt2$ нам подходит, очевидно, $a=-2\sqrt2$.
4) $a$, отвечающее за касание прямой $y=x+a$ и меньшей полуокружности находим из условия:
$D=0$ для $x^2+(x+a+1)^2=1.$
$D$ для $2x^2+2(a+1)x+a^2+2a=0$ – есть $-a^2-2a+1,$
поэтому требуем: $a^2+2a-1=0.$
Из двух вариантов $a=-1\pm \sqrt2$ нам подходит, очевидно, $a=-1+\sqrt2$.
Итак, три решения исходная система будет иметь при $a\in (-2\sqrt2;-2)\cup (-2;0]\cup${$-1+\sqrt2$}.
Ответ: $(-2\sqrt2;-2)\cup (-2;0]\cup${$-1+\sqrt2$}.
19.1. На доске написаны числа 1, 2, 3, …, 30. За один ход разрешается стереть произвольные три числа, сумма которых меньше 35 и отлична от каждой из сумм троек числа, стёртых на предыдущих ходах.
а) Приведите пример последовательности 5 ходов.
б) Можно ли сделать 10 ходов?
в) Какое наибольшее число ходов можно сделать?
Решение: + показать
а) Например,
$(1;10;23)$, сумма – $34;$
$(2;9;22)$, сумма – $33;$
$(3;8;21)$, сумма – $32;$
$(4;7;20)$, сумма – $31;$
$(5;6;19)$, сумма – $30.$
б) Допустим, можно сделать $10$ ходов. Тогда будем иметь $10$ троек, сумма чисел в каждой из которых меньше $35$. Тогда сумма чисел всех троек меньше $350.$ Но десять троек – это все $30$ чисел данного ряда. А сумма чисел $1;2;3;…;30$ – есть $\frac{1+30}{2}\cdot 30,$ то есть $465.$
Пришли к противоречию.
Нет, $10$ ходов сделать нельзя.
в) Как мы уже выяснили, $10$ ходов сделать нельзя.
Можно ли сделать $9$ ходов?
Нет. Сумма чисел, входящих в $9$ взятых троек меньше $315$. Во взятые $9$ троек чисел не вошли $3$ числа. Даже если эти числа – $30;29;28,$ то сумма чисел девяти троек и чисел $30;29;28$ меньше $315+30+29+28,$ то есть меньше $402$ (а должна быть $465$).
Можно ли сделать $8$ ходов?
Нет. Сумма чисел, входящих в $8$ взятых троек меньше $280$. Во взятые $8$ троек чисел не вошли $6$ чисел. Даже если эти числа – $30;29;28;27;26;25$ то сумма чисел восьми троек и чисел $30;29;28;27;26;25$ меньше $280+165,$ то есть меньше $445$ (а должна быть $465$).
Можно ли сделать $7$ ходов?
Нет. Сумма чисел, входящих в $7$ взятых троек меньше $35+34+…+29,$ то есть меньше $224$. Во взятые $7$ троек чисел не вошли $9$ чисел. Даже если эти числа – $30;29;…;22$ то сумма чисел семи троек и чисел $30;…;22$ меньше $224+234,$ то есть меньше $458$ (а должна быть $465$).
Можно сделать, например, таких $6$ ходов:
$(1;12;21)$, сумма – $34;$
$(2;11;20)$, сумма – $33;$
$(3;10;19)$, сумма – $32;$
$(4;9;18)$, сумма – $31;$
$(5;8;17)$, сумма – $30;$
$(6;7;16)$, сумма – $29.$
Ответ:
а) $(1;10;23)$, $(2;9;22),$ $(3;8;21),$ $(4;7;20)$, $(5;6;19).$
б) нет.
в) 6.
Задания (часть С) резервного дня сдачи ЕГЭ по математике 2016 можно найти здесь.















Елена Юрьевна,спасибо за оригинальное решение задания 15.Есть ли какое правило чтобы догадаться выделить целую часть?
Обычно, обращаюсь к выделению целой части, когда дробь «неправильная», то есть когда степень числителя больше или равна степени знаменателя.
Приведу несколько примеров рациональных неравенств, где этот прием значительно сократит решение неравенства:
[latexpage]$\frac{x^2-2x-2}{x^2-2x}+\frac{7x-19}{x-3}\leq \frac{8x+1}{x};$
$\frac{x^4-5x^3+3x-25}{x^2-5x}\geq x^2-\frac{1}{x-4}+\frac{5}{x};$
$x^3+6x^2+\frac{-8x^2+4x+16}{x+4}\leq 4.$
Я внёс новую переменную сразу и решил, как обычное неравенство. А далее, раскрыл, как полагается!
Елена Юрьевна,спасибо за все.Хранит Вас БОГ.
Спасибо :D :D :D !
18.2 оригинальное решение и очень краткое. Супер! Спасибо. Я пробовал заморочится графическим методом, запутался и ничего у меня не получилось.
Да, Василий. Думаю, если не увидеть полный квадрат, можно долго провозиться… И, надо сказать, выделение его – далеко не очевидно… Жаль, тех учеников, что решают параметры, но не смогли справиться с этим заданием(((
Добрый день, Елена Юрьевна! Можно рассмотреть решение №14.1. векторным методом? Спасибо!
Ирина, рассмотрела (добавила). Но очень кратко…
Елена Юрьевна, в задаче 14.1: Пусть Н проекция М на АВС (N – середина АС??)
Конечно, H! Описка.
Нина, спасибо!
Спасибо огромное за подробное решение задач! Думаю, не хватило времени выпускникам решить задачи на высокий балл.
Да уж… каждая задача выполнима отдельно, но когда нужно решить их несколько, да качественно оформить, – задача не из легких для выпускников…
Василий, Нина! Спасибо за замеченные опечатки! Исправила. Но ваши комментарии «слетели» из-за технических работ на сайте…
за замеченные опечатки! Исправила. Но ваши комментарии «слетели» из-за технических работ на сайте… 
а почему вы не доказали в планиметрической задаче,что h=2h1,через подобие.нельзя же так перепрыгивать
Вано, пишите на ЕГЭ настолько подробно, насколько считаете нужным.
Скажите, почему в задаче 18.1 в качестве условия положительности обоих корней использовано то, что свободный член должен быть положительным?
Согласно теореме Виета произведение корней квадратного приведенного уравнения – свободный член. Да, безусловно, произведение двух отрицательных корней – также положительно, но это вариант исключается в сили того, что сумма корней – единица (коэффициент при переменной в первой степени).