Разбор отдельных заданий части С. Основная волна, 2 июня 2017
13.1. а) Решите уравнение $\large 8\cdot 16^{cosx}-6\cdot 4^{cosx}+1=0.$
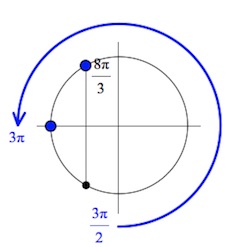
б) Найдите корни уравнения из отрезка $[\frac{3\pi}{2};3\pi].$
Решение: + показать
а)
$\large 8\cdot (4^{cosx})^2-6\cdot 4^{cosx}+1=0.$
Наблюдаем квадратного уравнение относительно $4^{cosx}.$
$\large 4^{cosx}=\frac{3\pm 1}{8};$
$\large 4^{cosx}=\frac{1}{2}$ или $\large 4^{cosx}=\frac{1}{4};$
$\large 4^{cosx}=4^{-\frac{1}{2}}$ или $\large 4^{cosx}=4^{-1};$
$cosx=-\frac{1}{2}$ или $ cosx=-1;$
$x=\pm \frac{2\pi}{3}+2\pi n$ или $x=\pi +2\pi n,$ $n\in Z.$
б) Корни уравнения из отрезка $[\frac{3\pi}{2};3\pi]:$
$\frac{8\pi}{3};3\pi.$
Ответ:
а) $\pm \frac{2\pi}{3}+2\pi n$; $\pi +2\pi n,$ $n\in Z;$
б) $\frac{8\pi}{3};3\pi.$
13.2. а) Решите уравнение $log_4(2^{2x}-\sqrt3cosx-sin2x)=x.$
б) Найдите корни уравнения из отрезка $[-\frac{\pi}{2};\frac{3\pi}{2}].$
Решение: + показать
а)
$log_4(2^{2x}-\sqrt3cosx-sin2x)=x;$
$log_4(2^{2x}-\sqrt3cosx-sin2x)=log_44^x;$
$4^{x}-\sqrt3cosx-sin2x=4^x;$
$\sqrt3cosx+sin2x=0;$
$\sqrt3cosx+2sinxcosx=0;$
$cosx(\sqrt3+2sinx)=0;$
$cosx=0$ или $sinx=-\frac{\sqrt3}{2};$
$x=\frac{\pi}{2}+\pi n$ или $x=-\frac{\pi}{3}+2\pi n$ или $x=-\frac{2\pi}{3}+2\pi n,$ $n\in Z.$
б) Корни уравнения из отрезка $[-\frac{\pi}{2};\frac{3\pi}{2}]:$
$-\frac{\pi}{2};-\frac{\pi}{3};\frac{\pi}{2};\frac{4\pi}{3};\frac{3\pi}{2}.$

Ответ:
а) $\frac{\pi}{2}+\pi n$, $-\frac{\pi}{3}+2\pi n$, $-\frac{2\pi}{3}+2\pi n,$ $n\in Z.$
б) $-\frac{\pi}{2};-\frac{\pi}{3};\frac{\pi}{2};\frac{4\pi}{3};\frac{3\pi}{2}.$
14.1. Дана пирамида $PABCD$, в основании которой – трапеция $ABCD$, причём $\angle BAD+\angle ADC=90^{\circ}.$
Плоскости $(PAB)$ и $(PCD)$ и перпендикулярны плоскости основания пирамиды.
Прямые $AB$ и $CD$ пересекаются в точке $K$.
а) Доказать, что $(PAB)\perp (PCD).$
б) Найти $V_{PKBC},$ если $AB=BC=CD=3,$ а высота пирамиды равна $8.$
Решение:+ показать
а) Заметим, так как $\angle BAD+\angle ADC=90^{\circ},$ то $\angle AKD=90^{\circ}.$
Прямая $AB,$ лежащая в $(ABC),$ перпендикулярна линии пересечения перпендикулярных плоскостей $ABC,PCD,$ а значит, по свойству перпендикулярных плоскостей, перпендикулярна плоскости $PCD.$
По признаку перпендикулярности плоскостей, раз плоскость $ABP$ содержит перпендикуляр $AB$ к плоскости $PCD,$ то плоскости $PAB,PCD$ перпендикулярны, что и требовалось доказать.

б) Как уже говорилось, $AB\perp PCD,$ значит, в частности, $AB\perp PK.$
Аналогично, используя то, что $CD\perp ABP,$ имеем, в частности, $CD\perp PK.$
То есть $PK$ перпендикулярна плоскости $ABC$ по признаку перпендикулярности прямой и плоскости.
Поскольку трапеция $ABCD$ равнобедренная, то $\angle KBC=\angle KCB,$ то есть прямоугольный треугольник $BCK$ – равнобедренный, и поскольку его гипотенуза равна $3$ согласно условию, то $BK=KC=\frac{3}{\sqrt2}.$
Итак, $V_{BCKP}=\frac{S_{BCK}\cdot PK}{3}=\frac{\frac{9}{4}\cdot 8}{3}=6.$
Ответ: $6$.
14.2. На ребрах $AB$ и $BC$ треугольной пирамиды $ABCD$ отмечены точки $M$ и $N$
соответственно, причем $AM:MB =CN:NB=1:3$. Точки $P$ и $Q$ – середины рёбер $DA$ и $DC$ соответственно.
а) Докажите, что точки $P,Q,M$ и $N$ лежат в одной плоскости.
б) Найдите, в каком отношении эта плоскость делит объем пирамиды.
Решение: + показать
a) $PQ$ – средняя линия треугольника $ACD,$ $PQ\parallel AC.$
Так как $AM:MB =CN:NB=1:3$, то $MN\parallel AC.$
По признаку параллельности прямых $PQ\parallel MN.$ Это означает, что точки $P,Q,M$ и $N$ лежат в одной плоскости.

б) $V_{ABCD}=\frac{S_{ABC}\cdot h}{3},$ где $h$ – высота, опущенная из $D$ на $ABC.$
Будем искать объем многогранника $AMNCQP$ как сумму объемов пирамид $AMNCQ,$ $APMQ.$
Треугольники $MBN,ABC$ подобны, коэффициент подобия – $\frac{3}{4}.$ Поэтому $S_{MBC}:S_{ABC}=9:16,$ то есть $S_{AMNC}=\frac{7}{16}S_{ABC}.$
Заметим, высота пирамиды $AMNCQ$ (основание – $AMNC$) – $\frac{h}{2}$ (из подобия треугольников $DHC,QTC$ с коэффициентом $\frac{1}{2}$ ($H,T$ – основания перпендикуляров к плоскости $ABC$ из $D,Q$)).
$V_{AMNCQ}=\frac{S_{AMNC}\cdot \frac{h}{2}}{3}=\frac{\frac{7}{16}S_{ABC}\cdot \frac{h}{2}}{3}=\frac{7}{32}V_{ABCD}.$
С другой стороны $V_{ABCD}=\frac{S_{ABD}\cdot h’}{3},$ где $h’$ – высота, опущенная из $C$ на $ABD.$
Заметим, высота пирамиды $APMQ$ (основание – $APM$) – $\frac{h’}{2}$ (аналогично рассуждениям выше).
Тогда
$V_{APMQ}=\frac{S_{APM}\cdot \frac{h’}{2}}{3}.$
Несложно заметить, $S_{APM}=\frac{1}{2}\cdot AP\cdot AM\cdot sin A=\frac{1}{2}\cdot \frac{AD}{2}\cdot \frac{AB}{4}\cdot sin A=\frac{1}{8}S_{ABD}.$
Стало быть, $V_{APMQ}=\frac{\frac{1}{8}S_{ABD}\cdot \frac{h’}{2}}{3}=\frac{1}{16}V_{ABCD}.$
Итак, $V_{AMNCQP}=\frac{7}{32}V_{ABCD}+\frac{1}{16}V_{ABCD}=\frac{9}{32}V_{ABCD}.$
При этом объем второго многогранника $MBNQPD$ есть $V_{ABCD}-\frac{9}{32}V_{ABCD}=\frac{23}{32}V_{ABCD}.$
Наконец, искомое отношение объемов многогранников – есть $9:23.$
Ответ: б) $9:23$.
14.3. Основанием прямой треугольной призмы $ABCA_1B_1C_1$ является прямоугольный треугольник $ABC$ с прямым углом $C$. Диагонали боковых граней $AA_1B_1B$ и $BB_1C_1C$ равны $15$ и $9$ соответственно, $AB=13.$
а) Докажите, что треугольник $BA_1C_1$ прямоугольный.
б) Найдите объем пирамиды $AA_1C_1B.$
Решение: + показать
a) $A_1C_1\perp B_1C_1$ по условию. $CC_1\perp A_1C_1$ (призма $ABCA_1B_1C_1$ – прямая). Тогда по признаку перпендикулярности прямой и плоскости $A_1C_1\perp CC_1B_1.$
Но тогда $A_1C_1\perp BC_1$ ($BC_1\in (CC_1B_1)$) по свойству прямой, перпендикулярной плоскости.
Итак, треугольник $A_1BC_1$ – прямоугольный.

б) Рассмотрим пирамиду $AA_1C_1B$ как пирамиду с основанием $A_1BC_1$.
Так как $AC\parallel A_1BC_1,$ то расстояние от $A$ до плоскости $A_1BC_1$ равно расстоянию от $C$ до $A_1BC_1$.
Построим в плоскости $CC_1B_1$ перпендикуляр $CH$ к $ BC_1.$ Поскольку при этом $A_1C_1$ – перпендикуляр к $CC_1B_1,$ то $A_1C_1\perp CH.$ Итак, $CH\perp (A_1BC_1),$ длина $CH$ – длина высоты пирамиды $AA_1C_1B$, опущенной из $A$ на $A_1BC_1$.
Так как $A_1C_1=\sqrt{15^2-9^2}=12,$ то $S_{A_1BC_1}=54.$
Поскольку $S_{BCC_1}=\frac{CB\cdot CC_1}{2}=\frac{CH\cdot C_1B}{2},$ то $CH=\frac{CC_1\cdot CB}{C_1B}.$
Далее,
$BC=\sqrt{AB^2-AC^2}=\sqrt{13^2-12^2}=5;$
$CC_1=\sqrt{BC_1^2-BC^2}=\sqrt{9^2-5^2}=2\sqrt{14};$
$CH=\frac{2\sqrt{14}\cdot 5}{9}=\frac{10\sqrt{14}}{9}.$
Итак, $V_{AA_1C_1B}=\frac{S_{A_1BC_1}\cdot CH}{3}=\frac{54\cdot \frac{10\sqrt{14}}{9}}{3}=20\sqrt{14}.$
Ответ: $20\sqrt{14}.$
15.1. Решить неравенство
$\frac{log_2(4x^2)+35}{log_2^2x-36}\geq -1.$
Решение: + показать
$\frac{log_2(4x^2)+35}{log_2^2x-36}\geq -1;$
$\frac{log_2(4x^2)+35+log_2^2x-36}{log_2^2x-36}\geq 0;$
$\frac{log_2^2x+log_2(4x^2)-1}{log_2^2x-36}\geq 0;$
$\frac{log_2^2x+(2+log_2x^2)-1}{log_2^2x-36}\geq 0;$
$\frac{log_2^2x+2log_2|x|+1}{log_2^2x-36}\geq 0;$
$\frac{(log_2x+1)^2}{(log_2x-6)(log_2x+6)}\geq 0;$
Применяем метод замены множителей:
$\frac{(log_2x-log_2\frac{1}{2})^2}{(log_2x-log_264)(log_2x-log_2\frac{1}{64})}\geq 0;$
$\frac{(x-\frac{1}{2})^2}{(x-64)(x-\frac{1}{64})}\geq 0,$ $x>0;$

$x\in (0;\frac{1}{64})\cup${$\frac{1}{2}$}$\cup (64;+\infty).$
Ответ: $(0;\frac{1}{64})\cup${$\frac{1}{2}$}$\cup (64;+\infty).$
15.2. Решить неравенство
$\frac{log_4(64x)}{log_4x-3}+\frac{log_4x-3}{log_4(64x)}\geq \frac{log_4x^4+16}{log_4^2x-9}.$
Решение: + показать
$\frac{log_4(64x)}{log_4x-3}+\frac{log_4x-3}{log_4(64x)}\geq \frac{log_4x^4+16}{log_4^2x-9};$
$\frac{3+log_4x}{log_4x-3}+\frac{log_4x-3}{3+log_4x}\geq \frac{4log_4x+16}{(log_4x-3)(log_4x+3)}.$
Пусть $log_4x=m.$
$\frac{3+m}{m-3}+\frac{m-3}{3+m}\geq \frac{4m+16}{(m-3)(m+3)};$
$\frac{(m+3)^2+(m-3)^2-4m-16}{(m-3)(m+3)}\geq 0;$
$\frac{m^2-2m+1}{(m-3)(m+3)}\geq 0;$
$\frac{(m-1)^2}{(m-3)(m+3)}\geq 0.$
Обратная замена:
$\frac{(log_4x-1)^2}{(log_4x-3)(log_4x+3)}\geq 0;$
$\frac{(log_4x-log_44)^2}{(log_4x-log_464)(log_4x-log_4\frac{1}{64})}\geq 0;$
Применяем метод замены множителей:
$\frac{(x-4)^2}{(x-64)(x-\frac{1}{64})}\geq 0,$ $x>0;$

$x\in (0;\frac{1}{64})\cup${$4$}$\cup (64;+\infty).$
Ответ: $(0;\frac{1}{64})\cup${$4$}$\cup (64;+\infty).$
16.1. Точка $E$ – середина боковой стороны $CD$ трапеции $ABCD.$ На стороне $AB$ отмечена точка $K$ так, что $CK\parallel AE.$ Прямые $CK,BE$ пересекаются в точке $O.$
а) Докажите, что $CO=OK.$
б) Найдите отношение оснований трапеции $BC$ и $AD,$ если площадь треугольника $BCK$ составляет $\frac{9}{64}$ площади трапеции $ABCD.$
Решение: + показать
а) Пусть $F$– точка пересечения $AB,DC.$
Пусть $BF=x, FC=y.$
Пусть коэффициент подобия $\Delta BFC,\Delta AFD$ – $k$.
Тогда $AF=kx,FD=ky.$
С учетом того, что $E$ – середина $CD,$ имеем: $CE=ED=\frac{y(k-1)}{2}.$
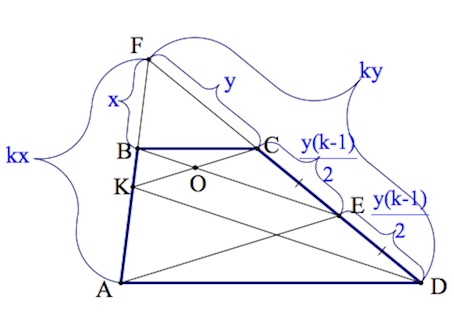
Треугольники $FKC,FAE$ подобны по двум углам (угол $F$ – общий, углы $FKC,FAE$ равны как соответственные углы при параллельных прямых $KC,AE$ и секущей $AB$).
Тогда
$\frac{FK}{FA}=\frac{FC}{FE};$
$\frac{FK}{kx}=\frac{y}{y+\frac{y(k-1)}{2}};$
$FK=\frac{2kx}{1+k};$
Замечаем, что $FB:FK=FE:FD.$ Действительно,
$\frac{x}{\frac{2kx}{1+k}}=\frac{y+\frac{y(k-1)}{2}}{ky};$
$\frac{x}{\frac{2kx}{1+k}}=\frac{y+yk}{2ky};$
$\frac{k+1}{2k}=\frac{k+1}{2k}.$
Учитывая, что у треугольников $FKD,FBE$ общий угол $F$ и $FB:FK=FE:FD$, получаем, что $\Delta FKD$ подобен $\Delta FBE.$ Откуда $BE\parallel KD.$
Тогда по теореме о пропорциональных отрезках $CE:ED=CO:OK.$ Так как $CE=ED,$ то и $CO=OK.$
Что и требовалось доказать.
б) Если $S$ – площадь треугольника $BCF,$ то в силу подобия $BCF,ADF$
$S_{AFD}=k^2S$ ($k$ – из пункта (a)).
Тогда $S_{ABCD}=S(k^2-1)$.
Согласно условию $S_{BCK}=\frac{9S(k^2-1)}{64}.$
Так как $\frac{S_{BCF}}{S_{BCK}}=\frac{BF}{BK},$ то, используя данные пункта (а), получаем:
$\frac{S_{BCF}}{S_{BCK}}=\frac{k+1}{k-1}.$
Далее,
$\frac{S}{\frac{9S(k^2-1)}{64}}=\frac{k+1}{k-1};$
$\frac{64}{9(k^2-1)}=\frac{k+1}{k-1};$
$\frac{64}{9(k+1)}=k+1;$
$(k+1)^2=\frac{64}{9};$
$k=\frac{5}{3}.$
Итак, $BC:AD=3:5.$
Ответ: $3:5.$
16.2. Две окружности с центрами $O_1$ и $O_2$ пересекаются в точках $A$ и $B$, причём точки $O_1$ и $O_2$ лежат по разные стороны от прямой $AB$. Продолжения диаметра $CA$ первой окружности и хорды $CB$ этой окружности пересекают вторую окружности в точках $D$ и $E$ соответственно.
а) Докажите, что треугольники $CBD$ и $O_1AO_2$ подобны.
б) Найдите $AD$, если $\angle DAE=\angle BAC,$ радиус второй окружности втрое больше радиуса первой и $AB=3$.
Решение: + показать
а) Линия центров $O_1O_2$ перпендикулярна прямой $AB.$ Действительно, из равенства треугольников $O_1AO_2, O_1BO_2$ по трем сторонам вытекает равенство углов, например, $AO_1O_2,BO_1O_2;$ равенство указаных углов говорит о том, что $O_1O_2$ содержит биссектрису угла $O_1$ треугольника $ABO_1,$ а поскольку треугольник $ABO_1$ равнобедренный, то $O_1O_2\perp AB.$
Угол $B$ опирается на диаметр $AC$ первой окружности, поэтому $\angle B=90^{\circ}.$ То есть и $CB\perp AB.$
Имеем: $O_1O_2\parallel CE.$
Откуда $\angle AO_1O_2=\angle ACB.$
Также замечаем, что вписанный и центральный углы $ADB,AO_2B$ опираются на одну дугу, то есть $2\angle ADB=\angle AO_2B.$ $O_2O_1$ – биссектриса угла $AO_2B,$ потому $\angle ADB=\angle AO_2O_1.$
Итак, треугольники $CBD$ и $O_1AO_2$ подобны по двум углам.

б) Очевидно, $AE$ – диаметр второй окружности (угол $B$ – прямой, опирается на $AE$).
Треугольники $ADE,ABC$ подобны по двум углам ($\angle B=\angle D=90^{\circ},\angle DAE=\angle BAC$ по условию).
$\frac{AE}{AC}=\frac{AD}{AB};$
$3=\frac{AD}{3};$
$AD=9.$
Ответ: б) $9.$
16.3. Основания трапеции равны $4$ и $9$, а её диагонали равны $5$ и $12$.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите высоту трапеции.
Решение: + показать
a) Проведем через точку $C$ прямую, параллельную $BD.$ Пусть она пересекает $AD$ в точке $K.$ Четырехугольник $BCKD$ – параллелограмм (по признаку параллелограмма).
Замечаем, в треугольнике $ACK$ $AC=5, CK=12,AK=13,$ при этом $13^2=5^2+12^2.$ По теореме, обратной теореме Пифагора, треугольник $ACK$ – прямоугольный (угол $ACK$ – прямой).
$\angle ACK=\angle AOD$ ($O$ – точка пересечения диагоналей трапеции) как соответственные углы при параллельных прямых $BD,CK$ и секущей $AC.$
Итак, диагонали трапеции перпендикулярны.

б) Высота $h$ трапеции $ABCD$ – высота треугольника $ACK$, проведенная к гипотенузе $AK.$
Так как $S_{ACK}=\frac{AC\cdot CK}{2}=\frac{h\cdot AK}{2}$, то $h=\frac{5\cdot 12}{13}=\frac{60}{13}.$
Ответ: б) $\frac{60}{13}.$
17.1. В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
− каждый январь долг увеличивается на $r$% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплачивать одним платежом часть долга.
Если ежегодно выплачивать по $58564$ рублей, то кредит будет полностью погашен за $4$ года, а если ежегодно выплачивать по $106964$ рублей, то кредит будет полностью погашен за $2$ года. Найдите $r$.
Решение:+ показать
Пусть кредит взят на сумму $x$ рублей.
Пусть $a=58564,b=106964.$
Поскольку банковский процент – $r$, то каждый январь остаток долга будет умножаться на коэффициент $\frac{r+100}{100},$ назовем его $p.$
Первая схема
В первый год после действия процента и первой выплаты в $a$ рублей на счету останется:
$px-a$ рублей,
во второй год после действия процента и выплаты в $a$ рублей на счету останется:
$p^2x-pa$ рублей
и так далее.
Наконец, четвертой выплатой в $a$ рублей кредит полностью погашается:
$p^4x-p^3a-p^2a-pa-a=0$ (1)
Вторая схема
В первый год после действия процента и первой выплаты в $b$ рублей на счету останется:
$px-b$ рублей,
Второй выплатой в $b$ рублей кредит полностью погашается:
$p^2x-pb-b=0$ (2)
Итак, из (1)
$p^4x=a(p^3+p^2+p+1),$
а из (2)
$p^2x=b(p+1).$
Тогда
$\frac{p^4x}{p^2x}=\frac{ a(p^3+p^2+p+1)}{b(p+1)};$
$bp^2(p+1)=a(p^3+p^2+p+1);$
$bp^2(p+1)=a(p+1)(p^2+1);$
$bp^2=a(p^2+1);$
$106964p^2=58564p^2+58564;$
$48400p^2=58564;$
$p^2=\frac{121}{100};$
$p=\frac{11}{10}.$
Откуда
$\frac{r+100}{100}=\frac{11}{10};$
$r=10.$
Ответ: $10.$
17.2. В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:
– в январе каждого года долг увеличивается на $30$% по сравнению с предыдущим годом
– с февраля по июнь нужно выплатить часть долга одним платежом. Определите, на какую сумму взяли в кредит в банке, если известно, что кредит был выплачен тремя равными платежами (за 3 года) и общая сумма выплат на $156060$ рублей больше суммы взятого кредита.
Решение:+ показать
Пусть кредит был взят на сумму $x$ рублей.
После первого действия процента на счету окажется $1,3x$ рублей.
Пусть размер платежа – $y$ рублей.
Тогда после первой выплаты долг составит $(1,3\cdot x-y)$ рублей.
Процент срабатывает второй раз, на счету – $(1,3^2\cdot x-1,3\cdot y).$ После второй выплаты долг составит $(1,3^2\cdot x-1,3\cdot y-y)$ рублей.
Процент срабатывает третий раз, на счету – $(1,3^3\cdot x-1,3^2\cdot y-1,3\cdot y).$
Кредит был выплачен тремя равными платежами (за три года), потому
$1,3^3\cdot x-1,3^2\cdot y-1,3\cdot y-y=0.$
При этом согласно условию $3y=x+156060.$
Тогда
$1,3^3\cdot (3y-156060)=y(1,3^2+1,3+1);$
$2,601y=1,3^3\cdot 156060;$
$y=131820.$
Откуда $x=3\cdot 131820-156060=239400$ рублей.
Ответ: $239400.$
17.3. В июле планируется взять кредит в банке на сумму $18$ млн. рублей на неко- торый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на $10$% по сравнению с концом преды- дущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если общая сумма выплат после полного погашения кредита составила $27$ млн. рублей?
Решение:+ показать
Пусть кредит был взят на $n$ лет.
Первая выплата составила $\frac{18}{n}+0,1\cdot 18.$
Вторая выплата составила $\frac{18}{n}+0,1\cdot \frac{18(n-1)}{n}.$
Третья выплата составила $\frac{18}{n}+0,1\cdot \frac{18(n-2)}{n}.$
И так далее…
Последняя выплата составила $\frac{18}{n}+0,1\cdot \frac{18}{n}.$
Общая сумма выплат:
$n\cdot \frac{18}{n}+\frac{0,1\cdot 18}{n}(n+(n-1)+(n-2)+…+1)=18+1,8\cdot \frac{n+1}{2}\cdot n=18+0,9(n+1).$
По условию общая сумма выплат после полного погашения кредита составила $27$ млн. рублей, поэтому
$18+0,9(n+1)=27;$
$0,9(n+1)=9;$
$n=9.$
Ответ: $9.$
18.1. Найти все значения параметра $a$, при каждом из которых уравнение
$\sqrt{5x-3}\cdot ln(x^2-6x+10-a^2)=0$
имеет ровно один корень на отрезке $[0;3].$
Решение:+ показать
Необходимо найти значения $a$, при которых данная система
$\begin{cases}\left[\begin{array}{rcl}5x-3=0,\\ln(x^2-6x+10-a^2)=0;\end{array}\right.\\\frac{3}{5}\leq x\leq 3,\\x^2-6x+10-a^2>0;&\end{cases}$
имеет одно решение.
$\begin{cases}\left[\begin{array}{rcl}x=\frac{3}{5},\\(x-3)^2=a^2;\end{array}\right.\\\frac{3}{5}\leq x\leq 3,\\x^2-6x+10-a^2>0;&\end{cases}$
$\begin{cases}\left[\begin{array}{rcl}x=\frac{3}{5},\\ x=3\pm a;\end{array}\right.\\\frac{3}{5}\leq x\leq 3,\\x^2-6x+10-a^2>0;&\end{cases}$
Заметим, $x=3\pm a$ удовлетворяют последней строке системы.
Случай 1
$x=\frac{3}{5}$ – единственное решение системы.
Тогда
$\begin{cases}(\frac{3}{5}-3)^2+1-a^2>0,\\\left[\begin{array}{rcl}3-a>3,\\ 3-a\leq \frac{3}{5};\end{array}\right.\\\left[\begin{array}{crl}3+a>3,\\ 3+a\leq \frac{3}{5};\end{array}\right.&\end{cases}$
$\begin{cases}(a-\frac{13}{5})(a+\frac{13}{5})<0,\\\left[\begin{array}{rcl}a<0,\\ a\geq\frac{12}{5};;\end{array}\right.\\\left[\begin{array}{crl}a>0,\\ a\leq-\frac{12}{5};\end{array}\right.&\end{cases}$

$a\in (-2,6;-2,4]\cup [2,4;2,6).$
Случай 2
$x=3-a$ – единственное решение системы.
Тогда
$\begin{cases}(\frac{3}{5}-3)^2+1-a^2\leq 0,\\\frac{3}{5}\leq 3-a\leq 3,\\\left[\begin{array}{rcl}3+a>3,\\ 3+a<\frac{3}{5};\end{array}\right.&\end{cases}$
$\begin{cases}(a-\frac{13}{5})(a+\frac{13}{5})\geq 0,\\0\leq a\leq \frac{12}{5},\\\left[\begin{array}{rcl}a>0,\\ a<-\frac{12}{5};\end{array}\right.&\end{cases}$
Нет значений $a$, отвечающих системе.
Случай 3
$x=3+a$ – единственное решение системы.
Тогда
$\begin{cases}(\frac{13}{5}-3)^2+1-a^2\leq 0,\\\frac{3}{5}\leq 3+a\leq 3,\\\left[\begin{array}{rcl}3-a>3,\\ 3-a<\frac{3}{5};\end{array}\right.&\end{cases}$
$\begin{cases}(a-\frac{13}{5})(a+\frac{13}{5})\geq 0,\\-\frac{12}{5}\leq a\leq 0,\\\left[\begin{array}{rcl}a<0,\\ a>\frac{12}{5};\end{array}\right.&\end{cases}$
Нет значений $a$, отвечающих системе.
Итак, $a\in (-2,6;-2,4]\cup [2,4;2,6).$
Ответ: $(-2,6;-2,4]\cup [2,4;2,6).$
19.1. На доске написано $30$ различных натуральных чисел, десятичная запись каждого из которых оканчивается или на цифру $2$, или на цифру $6$. Сумма написанных чисел равна $2454$.
а) Может ли на доске быть поровну чисел, оканчивающихся на $2$ и на $6$.
б) Может ли ровно одно число на доске оканчивается на $6$?
в) Какое наименьшее количество чисел, оканчивающихся на $6$, может быть записано на доске?
Решение: + показать
а) Нет, на доске не может быть написано поровну чисел, оканчивающихся на $2$ и на $6$. В противном случае сумма таких чисел оканчивалась бы на $0$ $(15\cdot 2+15\cdot 6=120),$ что противоречит условию.
б) Нет, среди чисел на доске не может ровно одно число заканчиваться на $6.$ Это бы означало, что $29$ чисел должно оканчиваться на $2$. Но даже если брать $2;12;22;…,$ то сумма $29$ таких слагаемых будет $\frac{(2+282)\cdot 29}{2},$ то есть $4118,$ что больше $2454.$
в) Определим, какое наибольшее количество чисел, оканчивающихся на $2$ может быть записано на доске.
Пусть на доске $n$ чисел, оканчивающихся на $2.$ Сумма $n$ таких чисел будет не меньше суммы набора $2;12;22;..;2+10(n-1).$
Решим неравенство:
$\frac{2+10n-8}{2}\cdot n\leq 2454;$
$(5n-3)n\leq 2454;$
$5n^2-3n-2454\leq 0;$
$(n-\frac{3+\sqrt{49089}}{10})(n-\frac{3-\sqrt{49089}}{10})\leq 0.$
Вторая скобка неравенства положительна.
$n-\frac{3+\sqrt{49089}}{10}\leq 0;$
Так как $220=\sqrt{48400}<\sqrt{49089}<\sqrt{49284}=222,$ то $22,3<\frac{3+\sqrt{48649}}{10}<22,5.$
Наибольшее натуральное $n,$ отвечающее неравенству, – это $22.$
Если мы берем $n=22,$ то сумма всех чисел должна оканчиваться на $2,$ так как $22\cdot 2+8\cdot 6=92,$ что противоречит условию.
При $n=21$ сумма всех чисел должна оканчиваться на $6,$ так как $21\cdot 2+9\cdot 6=96,$ что противоречит условию.
При $n=20$ сумма всех чисел должна оканчиваться на $0,$ так как $20\cdot 2+10\cdot 6=100,$ что противоречит условию.
Подберем вариант, когда $n=19:$
$6;16;26;…;96;196;2;12;…;182$.
Ответ: а) нет; б) нет; в) $11.$














Здравствуйте, Елена Юрьеана! Нет ли опечатки в условии задачи 16.1? А именно: а) СО=СК?
Нина, спасибо большое! Подправила.
Спасибо большое!
Здравствуйте, Елена Юрьевна. В задании 15.1 по ОДЗ х больше 0 должен ведь быть.
Ну это только я так могу – написать одз в самом решении, пометить на картинке, но не записать в ответе… Кошмар!
Кошмар!
У меня проблемы с сайтом были, не выдержал нагрузку, – загружался через раз, через два… все внимание рассеялось…
Спасибо!
Добрый день, Елена Юрьевна. Хочется поделиться своим решением пункта а) задачи 14. К сожалению, у меня не получилось скопировать чертёж. Попробую “на пальцах”. Продолжим ВЕ до пересечения с АD в точке Р. Тогда получится две пары подобных треугольников ВОСи РЕА, КВО АВЕ. Из первой пары ОС = АЕ*ОВ/РЕ, из второй ОК= АЕ*ОВ/ВЕ, но РЕ=ВЕ, т. к. треугольники ВСЕ и РDE равны, значит, ОС = ОК.
.
Так как ВСЕ = PDE, то ВЕ = РЕ.
Значит, ОС = ОК.
Простите, задача-то 16.
Татьяна, спасибо большое!
Елена Юрьевна, здравствуйте! Задача 14.2: Треугольники МВС(MBN?) и АВС подобны. И далее в отношении площадей – МВN.
Спасибо Вам огромное.
Нина, спасибо большое!
а в 13.2 делить на 4 в степени х это законно? нужно ли как-то проверять на потерю корней?
Деление на 4^x не производилось! Читайте внимательней!