Разбор заданий резервного дня сдачи ЕГЭ по математике от 28 июня 2017

а)

$log_2(x^2-14x)=5;$

$log_2(x^2-14x)=log_232;$

$x^2-14x=32;$

$x=7\pm \sqrt{49+32};$

$x=16$ или $x=-2.$

б) Найдем корни уравнения из  отрезка $[log_30,1;5\sqrt 10]:$

$16=\sqrt{256}>5\sqrt{10}=\sqrt{250},$ поэтому $16$ не входит в указанный отрезок.

$5\sqrt{10}>-2=log_33^{-2}=log_3\frac{1}{9}>log_3\frac{1}{10},$ поэтому $-2$ принадлежит указанному отрезку.

Ответ: а) $-2;16;$ б) $-2.$  

а) Проекция наклонной $PA$ на плоскость основания $ABC$ – это $AC.$ Раз по условию  наклонная $PA$ перпендикулярна прямой $BC$ плоскости $ABC,$ то и ее проекция $AC$ перпендикулярна $BC$ по теореме о трех перпендикулярах.

Итак, треугольник $ABC$ – прямоугольный ($\angle C=90^{\circ}$.)

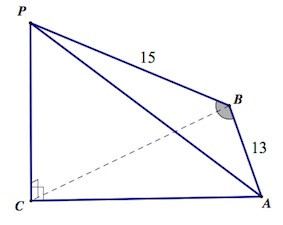
б) Из треугольника $ABP$ по теореме косинусов:

$AP^2=15^2+13^2-2\cdot 15\cdot 13\cdot \frac{48}{65}=106.$

Пусть $PC=x.$

Тогда из $\Delta PBC$   $BC^2=225-x^2$   и  из $\Delta PCA$   $AC^2=106-x^2.$

Для $\Delta ABC$ по теореме Пифагора:

$169=225-x^2+106-x^2;$

$x^2=81;$

$x=9.$

Итак, $V_{PABC}=\frac {1}{3}\cdot S_{ABC}\cdot PC=\frac{\frac{12\cdot 5}{2}\cdot 9}{3}=90.$

Ответ: б) $90.$ 

$(3^{4x-x^2-1})^2-36\cdot 3^{4x-x^2-1}+243\geq 0;$

$(3^{4x-x^2-1}-27)(3^{4x-x^2-1}-9)\geq 0;$

$(3^{4x-x^2-1}-3^3)(3^{4x-x^2-1}-3^2)\geq 0;$

$(4x-x^2-1-3)(4x-x^2-1-2)\geq 0;$

 $(x^2-4x+4)(x^2-4x+3)\geq 0;$

 $(x-2)^2(x-3)(x-1)\geq 0;$

$x\in (-\infty;1]\cup$ {$2$}$\cup[3;+\infty).$

Ответ: $(-\infty;1]\cup$ {$2$}$\cup[3;+\infty).$ 

$\frac{1}{3^x-1}+\frac{9^{x+\frac{1}{2}}-3^{x+3}+3}{3^x-9}\geq 3^{x+1};$

$\frac{1}{3^x-1}+\frac{3\cdot 9^x-27\cdot 3^{x}+3}{3^x-9}\geq 3^{x+1};$

$\frac{1}{3^x-1}+3\cdot \frac {9^x-9\cdot 3^{x}+1}{3^x-9}\geq 3^{x+1};$

$\frac{1}{3^x-1}+3\cdot \frac {3^x\cdot (3^x-9)+1}{3^x-9}\geq 3^{x+1};$

$\frac{1}{3^x-1}+3^{x+1}+\frac{3}{3^x-9}\geq 3^{x+1};$

$\frac{1}{3^x-1}+\frac{3}{3^x-9}\geq 0;$

$\frac{3^x-9+3\cdot 3^x-3}{(3^x-1)(3^x-9)}\geq 0;$

$\frac{4\cdot (3^x-3)}{(3^x-1)(3^x-9)}\geq 0;$

$\frac{x-1}{x(x-2)}\geq 0;$

$x\in (0;1]\cup (2;+\infty).$

Ответ: $(0;1]\cup (2;+\infty).$

a) Пусть $T$ – точка касания вписанной в трапецию окружности со стороной $BC,$ $Q$ – точка касания окружности со стороной $AD.$

Пусть $x=MB,$ тогда $AM=8x,$ пусть $y=CN,$ тогда $DN=2y.$

По свойству отрезков касательных

$BT=MB=x,TC=CN=y,AM=AQ=8x,ND=QD=2y.$

Пусть $BH_1\perp AD,CH_2\perp AD.$

Из треугольника $ABH_1$  $BH_1^2=AB^2-AH_1^2,$ из треугольника $CDH_2$  $CH_2^2=CD^2-DH_2^2.$

Тогда

$(9x)^2-(7x)^2=(3y)^2-y^2;$

$y=2x.$

Стало быть, $BC=x+y=3x,$ $AD=8x+2y=12x,$ что означает, что $AD=4BC.$

Что и требовалось доказать.

б) Пусть $K$ – точка пересечения лучей $AB,DC.$

Треугольники $BKC,AKD$ подобны, $k=4.$

Тогда $BK=3x,KC=y=2x.$

По теореме Косинусов для треугольника $BKC:$

$BC^2=BK^2+CK^2-2\cdot BK\cdot CK\cdot cosK;$

$9x^2=9x^2+4x^2-2\cdot 3x\cdot 2x\cdot cosK;$

$cosK=\frac{1}{3}.$

По теореме Косинусов для треугольника $MNK:$

$MN^2=MK^2+NK^2-2\cdot MK\cdot NK\cdot cosK;$

$MN^2=16x^2+16x^2-2\cdot 4x\cdot 4x\cdot \frac{1}{3};$

$MN=\frac{8\sqrt x}{3}.$

При этом (замечая, что высота трапеции – два радиуса вписанной окружности) из треугольника $ABH_1$ по теореме Пифагора $81x^2-49x^2=(2\sqrt6)^2,$ откуда $x=\frac{\sqrt3}{2}.$

Наконец, $MN=\frac{8\sqrt3\cdot \frac{\sqrt3}{2}}{3}=4.$

Ответ: $4.$ 

a) Центр вписанной окружности – точка пересечения биссектрис углов трапеции. А как известно, биссектрисы соседних углов при основаниях трапеции пересекаются под прямым углом. Действительно, так как сумма углов $A$ и $B$ равна $180^{\circ},$ то сумма половин углов $A$ и $B$ равна $90^{\circ}$ ($\angle BAO+\angle ABO=90^{\circ}$), то есть $\angle AOB=90^{\circ}.$ Аналогично, $\angle COD=90^{\circ}.$

Но тогда и углы $AOD,BOC$ в сумме дают $180^{\circ},$ а значит

$sinAOD=sin(180^{\circ}-\angle BOC)=sinBOC.$

Что и требовалось доказать.

б) Так как трапеция $ABCD$ – описанная, то $AB+CD=BC+AD=12.$ Пусть $AB=x,$ тогда $CD=12-x.$

Пусть $CH$ – высота трапеции. Тогда $HD=AD-BC=2.$

Заметим также, что $CH=AB=x.$

По теореме Пифагора для треугольника $CDH:$

$(12-x)^2=x^2+2^2;$

$x=\frac{35}{6}.$

Тогда $S_{ABCD}=\frac{BC+AD}{2}\cdot AB=\frac{5+7}{2}\cdot \frac{35}{6}=35.$

Ответ: б) $35.$ 

Пусть на первом заводе рабочие трудятся суммарно $x^2$ часов в неделю, на втором заводе – $y^2$ часов. Тогда произведено будет за неделю $x+y$ единиц товара.

Вадим должен заплатить $200x^2+300y^2$ рублей, значит

$200x^2+300y^2=1200000$

или

$2x^2+3y^2=12000.$

Откуда

$y=\sqrt{\frac{12000-2x^2}{3}}.$

Необходимо, чтобы сумма $x+\sqrt{\frac{12000-2x^2}{3}}$ была бы наибольшей.

Исследуем функцию $f(x)=x+\sqrt{\frac{12000-2x^2}{3}}$ на наибольшее значение на $[0;20\sqrt{15}].$ Это наибольшее значение функции и будет отвечать за наибольшее количество единиц товара, которое можно произвести за неделю на двух заводах.

$f'(x)=1-\frac{4x}{6\sqrt{\frac{12000-2x^2}{3}}}=\frac{3\sqrt{\frac{12000-2x^2}{3}}-2x}{3\sqrt{\frac{12000-2x^2}{3}}}.$

$x=60$ – точка экстремума.

Так как $f(0)=20,f(20\sqrt{15})=20\sqrt{15},f(60)=100,$ то есть $100$ – максимальное значение среди значений функции на концах отрезка и в точке экстремума, то $100$ – и есть наибольшее значение функции  $f(x)$ на $[0;20\sqrt{15}].$

Ответ: $100.$ 

$x\sqrt{x-a}=\sqrt{4x^2-4ax-2x+2a};$

$x\sqrt{x-a}=\sqrt{4x(x-a)-2(x-a)};$

$x\sqrt{x-a}=\sqrt{(x-a)(4x-2)}.$

$\left[\begin{array}{rcl}x=a,\\\begin{cases}a<x,\\x=\sqrt{4x-2};&\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}x=a,\\\begin{cases}a<x,\\x^2-4x+2=0;&\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}x=a,\\\begin{cases}a<x,\\x=2\pm \sqrt2;&\end{cases}\end{array}\right.$

Работаем в системе координат $(x;a)$. 

Становится видно, что исходное уравнение имеет ровно один корень на отрезке $[0;1]$ при

$a\in (-\infty;0)\cup [2-\sqrt2;1].$

Ответ: $(-\infty;0)\cup [2-\sqrt2;1].$

$\begin{cases}(y^2-xy+x-3y+2)\sqrt{x+3}=0,\\a-x-y=0;&\end{cases}$

Поскольку

$y^2-xy+x-3y-y+2=y^2-xy+x-2y-y+2=$

$=y(y-1)-x(y-1)-2(y-1)=(y-1)(y-x-2),$

то имеем

$\begin{cases}(y-1)(y-x-2)\sqrt{x+3}=0,\\a-x-y=0;&\end{cases}$

$\begin{cases}\left[\begin{array}{rcl}y=1,\\y=x+2,\\x=-3;\end{array}\right.&\\x\geq -3,\\y=-x+a;\end{cases}$

Ровно два различных решения исходная система будет иметь при  $a\in (-4;-2]\cup ${$0$}.

Ответ: $(-4;-2]\cup ${$0$}.

а) Число $2108124117$ могло быть получено из числа $2847$ указанным способом.

б) Число $374944128$ не могло получится из какого-либо числа указанным способом, так как иначе бы это означало, что $9=4+4.$

в) Пусть имеется трехзначное число $100a+10b+c.$ Поскольку нам интересно получение наибольшего нового  числа, то между каждыми соседними цифрами потребуем, чтобы приписывалось двузначное число.

Тогда новое число будет семизначным:

$10^6\cdot a+10^5+10^4\cdot (a+b-10)+10^3\cdot b+10^2+10\cdot (b+c-10)+c.$

Так как число делится на $11$, если  знакочередующаяся сумма его цифр делится на $11$, то необходимо, чтобы сумма

$a-1+(a+b-10)-b+1-(b+c-10)+c=2a-b$

делилась бы на $11.$

Пусть $a=9$ (при иных значениях искомое число будет меньше) тогда $b=7.$ Значение $c$ можно брать любое, – берем $9.$

Итак, взяв число $979,$ получим в итоге число $9167169,$ кратное $11.$

Ответ: а) $2847$; б) нет; в) $9167169.$

а) Пусть $a_4+a_5+a_6=m.$

Согласно условию $a_2+a_3+m=35,a_1+a_3+m=30.$ Откуда $a_2=a_1+5.$

Поскольку при этом $a_1+a_2+m=32,$ то $m=27-2a_1.$

Пусть, например, $a_1=1,$ тогда $a_2=6,a_3=4,m=25.$

Последовательность $1;6;4;9;9;7$ отвечает требованиям задачи.

б) Имеем:

$a_2+a_3+m=35$  и  $a_1+a_2+m=25.$

Тогда $a_3-a_1=10,$ что противоречит условию (ведь последовательность состоит из однозначных чисел).

Не существует такой последовательность, для которой $M_3=5$.

в) Поскольку $a_3\leq a_1+9,$ то, используя $a_2+a_3+m=35$, получаем:

$35=a_2+a_3+m\leq a_1+9+a_2+m,$ то есть $a_1+a_2+m\geq 26.$

Попробуем подобрать необходимые числа так, чтобы $a_1+a_2+m=26.$

Пусть $a_1=0,$ тогда $a_2=5,a_3=9.$ На роль $a_4,a_5,a_6$ можно взять, например, $9;9,3.$

Итак, наименьшее возможное значение $M_3$ – это $26:5$, то есть  $5,2.$

Ответ: а) $1;6;4;9;9;7$; б) нет; в) $5,2.$