Главная / 15 (С3) Неравенства

19 Мар 2015

Категория: 15 (С3) НеравенстваИррациональные выражения, уравнения и неравенстваЛогарифмыТ/P A. Ларина

Задание №17 Т/Р №109 А. Ларина

Елена Репина 2015-03-19 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №15»

Смотрите также №15, №16, №18, №19, №20.

Решите неравенство

$log_2(x^2-8x+6)\geq 2+\frac{1}{2}log_2(2x-1).$

Решение:

$log_2(x^2-8x+6)\geq 2+\frac{1}{2}log_2(2x-1);$

$log_2(x^2-8x+6)\geq log_24+log_2\sqrt{2x-1};$

$log_2(x^2-8x+6)\geq log_24\sqrt{2x-1};$

$x^2-8x+6\geq 4\sqrt{2x-1}, x\neq \frac{1}{2};$

Выделяем полные квадраты в каждой части неравенства:

$(x^2-6x+9)-2x-3\geq (2^2+4\sqrt{2x-1}+(2x-1))-4-(2x-1), x\neq \frac{1}{2};$

$(x-3)^2\geq (2+\sqrt{2x-1})^2, x\neq \frac{1}{2};$

Совершим следующий равносильный переход:

$|x-3|\geq |2+\sqrt{2x-1}|, x\neq \frac{1}{2}$

и решим неравенство графически.

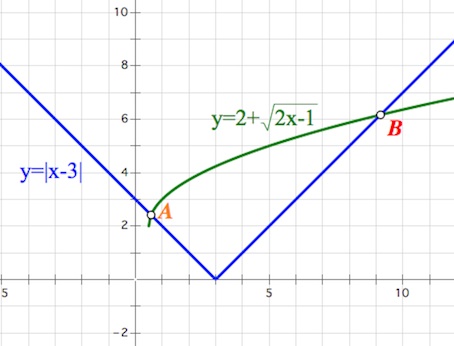
Найдем абсциссу точки $A$ (пересечение прямой $y=3-x$ и кривой $y=2+\sqrt{2x-1}$ ):

$3-x=2+\sqrt{2x-1};$

$1-x=\sqrt{2x-1};$

$1-2x+x^2=2x-1,1-x\geq 0;$

$x^2-4x+2=0, x\leq 1;$

$x=2-\sqrt2.$

Найдем абсциссу точки $B$ (пересечение прямой $y=x-3$ и кривой $y=2+\sqrt{2x-1}$ ):

$x-3=2+\sqrt{2x-1};$

$x-5=\sqrt{2x-1};$

$x^2-10x+25=2x-1,x-5\geq 0;$

$x^2-12x+26=0, x\geq 5;$

$x=6+\sqrt{10}.$

Итак, $x\in (\frac{1}{2};2-\sqrt2]\cup [6+\sqrt{10};+\infty).$

Ответ: $(\frac{1}{2};2-\sqrt2]\cup [6+\sqrt{10};+\infty).$

Автор: egeMax | комментария 4

Печать страницы

комментария 4

Дима

2015-04-04 в 17:11

Никогда бы не догадался до выделения полного квадрата.. Спасибо!

[ Ответить ]
- Дима
  
  2015-04-04 в 17:14
  
  А почему вы не учитываете условие ОДЗ для первого логарифма? Потому что, получается, что она больше корня => автоматически больше нуля?
  
  [ Ответить ]
  - egeMax
    
    2015-04-04 в 22:05
    
    Именно!
    
    [ Ответить ]
- egeMax
  
  2015-04-04 в 22:04
  
  Да, действия – не самые очевидные…
  Но от безвыходности приходится видеть полный квадрат…
  
  [ Ответить ]

Добавить комментарий Отменить ответ

Поиск по сайту
Материалы для подготовки к ЕГЭ
С1 С3 С5 С6
Рубрики
- 01 Простейшие текст/задачи (3)
- 02 Читаем графики (1)
- 03 Геометрия, ч. I (11)
- 04 Теория вероятностей (2)
- 05 Простейшие уравнения (5)
- 06 Геометрия, ч. II (11)
- 07 Производная, ПО (4)
- 08 Стереометрия (11)
- 09 Вычисления (6)
- 10 «Прикладные» задачи (4)
- 11 Текстовые задачи (7)
- 12 Исследование функции (2)
- 13 (С1) Уравнения (75)
- 14 (С2) Стереометр. задачи (90)
- 15 (С3) Неравенства (85)
- 16 (С4) Планиметр. задачи (81)
- 17 (С5) Практич. задачи (69)
- 18 (С6) Параметры* (76)
- 19 (С7) Числа, их свойства (36)
- Видеоуроки (42)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (53)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (38)
- Переменка (7)
- Планиметрия (75)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (82)
- Стереометрия (52)
- Т/P A. Ларина (437)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (68)
- Тригонометрические выражения, уравнения и неравенства (45)
- Функции и графики (9)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы